1.2. Итерационный алгоритм разбиения графа g с использованием чисел связности.
Сформулируем задачу компоновки КС как задачу разбиения графа G=(X,U) на подграфы Gi и Gj.
Подмножество ребер, попадающих в сечение (разрез графа) называется числом реберного соединения частей Gi и Gj графа G и обозначается Kij.
Задачей разбиения графа G=(X,U) является нахождение такой совокупности чисел, чтобы число реберного соединения графа G удовлетворяло заданному критерию оптимальности, а именно
- стремится к
минимуму
Задача разбиения графа на части относится к задачам, получение оптимального решения которых связано с полным перебором различных вариантов разбиения. Такой путь для конструктора неприемлем, так как он чрезвычайно затруднителен даже для современных быстродействующих ЭВМ.
Алгоритмы классифицируют по критериям, по ограничениям на формирование частей или по структуре вычислительной процедуры. С этой точки зрения их делят на последовательные (1), параллельно-последовательные (2) и итерационные (3).
1) Вводится последовательный процесс компоновки частей. На каждом шаге, которого в очередную часть добавляется один из элементов ММ, выбираемый по определенному приоритету.
2) Сначала выделяется некоторое исходное множество групп элементов, которое затем распределяется по частям с учетом критериев и ограничений на компоновку.
3) Сначала граф разбивается на определенное число ребер произвольным образом, например с помощью последовательных алгоритмов. Затем по некоторым правилам производится перестановка вершин из одной части в другую с целью минимизации числа внешних ребер.
Рассмотрим методику разбиения графа, заданного матрицей смежности на части с использованием чисел связности.
Для каждой вершины вводится числовая характеристика, которая оценивает связь рассматриваемой вершины с другими вершинами, лежащими внутри данного подграфа, по отношению к вершинам, находящимся вне его.
Назовем αK - числом связности вершины ХK
αк= { rK(Gi) - rK(Gj), если Хк є Xj [ Ф. 1.]
{ rK(Gj) - rK(Gi), если Хк є Xi
(Σ внешних ребер — Σ внутр. ребер)
rK(Gi) - число ребер, соединяющих вершины ХK с вершинами Gi=(Xi,Ui) rK(Gj) - число ребер, соединяющих вершину ХK с вершинами Gj=(Xj,Uj).
ФИЗИЧЕСКИЙ СМЫСЛ:
если α(Xi) = -1 означает, что при перестановке вершины Xi , лежащей в G1, в G2 число внешних ребер увеличится на 1.
α(Xj) = 0 означает, что перестановка вершин Xj из G1 в G2 оставит без изменения число соединительных ребер.
α(ХK) = 3 означает, что при переносе число соединительных ребер уменьшится на 3.
Для разбиения графа на два подграфа с минимизацией числа соединительных ребер с использованием чисел связности известна теорема.
ТЕОРЕМА:
Перестановка двух произвольных вершин ХK є Xi и X1 є Xj(Xi∩Xj)≠0 - приводим к уменьшению числа соединительных ребер между Gi и Gj, если:
а) вершина ХK не смежная с вершиной X1 и выполняется
неравенство αK + α1 > 0;
б) вершина ХK смежная с вершиной Xi и справедливо
неравенство αK + α1 > 2r1,K.
ЦЕЛЕВАЯ ФУНКЦИЯ:
Минимизация суммарного числа соединительных ребер.
Для более удобного определения подстановки строят матрицу:
в которой строки определяются вершинами из множества I , а столбцы - из множества Vi є N= {1,2,...,l-1}
На пересечении строки k строки (k є I) и q столбца (q є V) находится элемент:
[Ф.2.]
Элемент матрицы W ωk,q характеризует изменение числа соединительных ребер между Gi и Gj при перестановке вершин Xq є Xi и Хk є Xj.
Пример 1.
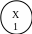
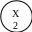
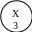
2
2
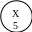
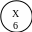
2
G=(X,U)
Исходный граф разбить на два подграфа: G1 (X1, U1) и G2 (X2, U2)
|X1| = 4
|X2| = 3
1) Строим матрицу смежности R0
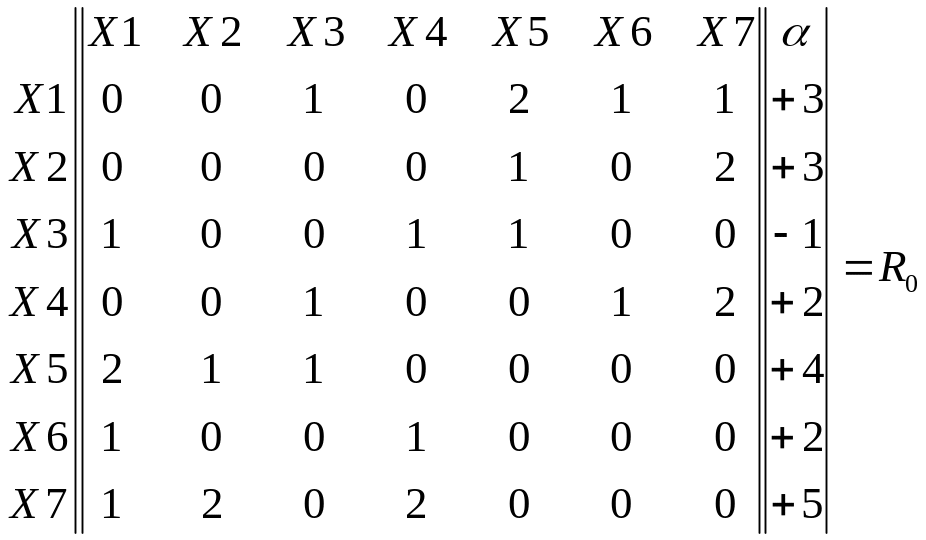
R1
R2
2) Разбиваем R0 на подматрицы R1 и R2 и определяем числа связности по формуле [Ф.1.].
Например: для вершины X1, находящейся в R1
α = 4 - 1= + 3.
3) Строим матрицу W0, определяя элементы матрицы по [Ф.2.] Например: для вершин X1 и Х5 (+3+4-2×2=+3)
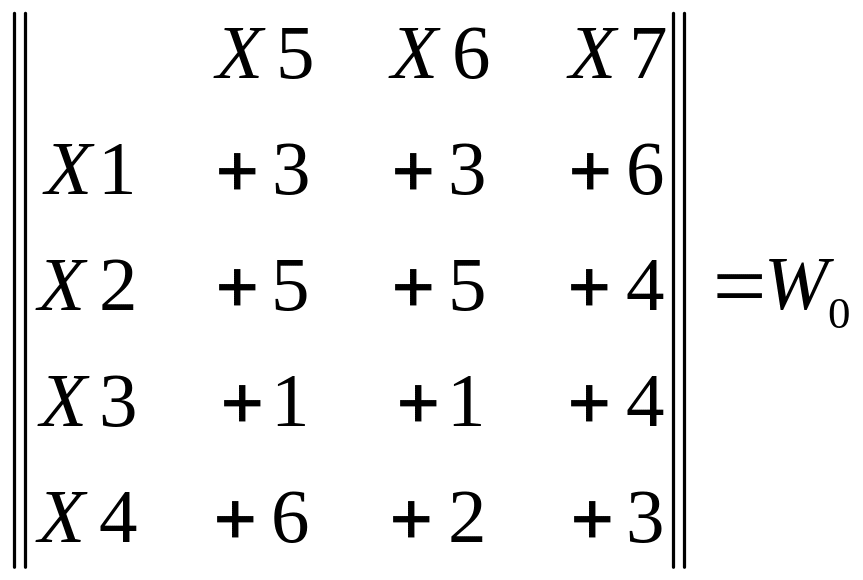
Из матрицы W0 получается, что для минимизации числа соединительных ребер между G1 и G2 графа G в матрице R0 необходимо переставить строки и столбцы X1 и Х7, поскольку ω1,7 = +6 матрицы W0 наибольший.
4) После выполнения указанной процедуры матрица R0 примет следующий вид:
Аналогично п.2 и п.3 определяем α и W0.
Меняем местами Х3 и Х6.
5
)
Теперь когда все числа αk,q≤0, строить матрицу W0 - не будем, т.к. в ней не найдется ни одного элемента ωk,q>0 и, следовательно, в графе G на данном шаге нет пары вершин, перестановка которых уменьшит Ki,j.
В результате получим: в матрицах R1 |X1| = 4
R2
|X2|
=
3
2
R1
2
R2
2