Основные законы теории цепей.
Рассмотрим основные законы теории цепей, а именно те, которые играют важную роль в построении ММ РЭС.
Законы Кирхгофа.
Узел схемы определяют как точку соединения 2-х и более элементов схемы. Каждый входящий в схему двухполюсник (элемент схемы с двумя выводами) называют ветвью.
Любую замкнутую часть цепи, состоящую из последовательного соединения двухполюсников и имеющую в качестве начального и конечного узла один и тот же узел, называют контуром.
Суть законов Кирхгофа покажем на примерах. Пусть дана схема, содержащая 4 четырехполюсника и 3 узла.
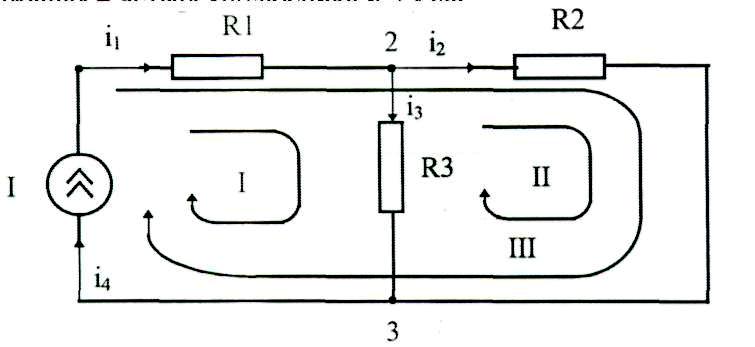
1. Зададим направления токов в этих элементах - ветвях. Тогда 1-й з-н Кирхгофа для токов (ЗКТ) формулируется следующим образом: алгебраическая сумма мгновенных значений токов, входящих и выходящих из любого узла, всегда равна нулю.
Для 1-го 2-го и 3-го узлов (условились писать входящие в узел токи с минусом, а входящие - с плюсом) следующие уравнения:
- I4+I1=0 - I1+I2+I3=0 - I3-I2+l4=0
Данная система уравнений однозначно описывает поведение электронной системы. Если известны номиналы сопротивления и тока источника тока, то можно определить i1, i2, i3.
2. Для построения полной ММ и определения всех неизвестных воспользуемся 2-м законом Кирхгофа для напряжений (ЗКН): алгебраическая сумма мгновенных значений падений напряжений на элементах по любому замкнутому контуру всегда равна нулю.
Условились: если заданное направление тока в ветви совпадает с направлением контура, то падение напряжения вносят со знаком плюс, в противном случае — минус.
Для контуров I, II, III
UI+U1+U3=0. U2-U3=0 U1+U2+UI=0
Последняя система уравнений также не позволяет вычислить все неизвестные, т. к. неизвестных - 4, уравнений - 3. Только решение всех уравнений, полученных на основе ЗНК и ЗКТ обеспечит определение неизвестных: i1, i2, i3, U1, U2, UI, U3.
Рассмотрим цепь
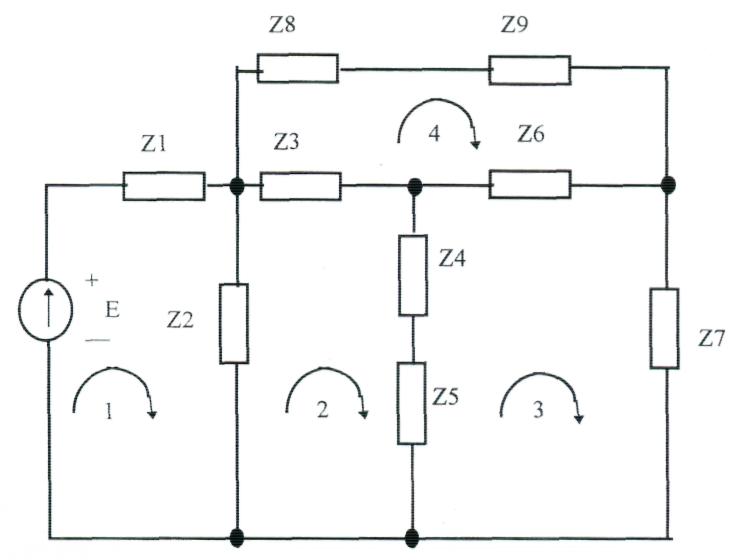
Можно выбрать множество различных замкнутых контуров, проходящих через элементы цепи. Выберем замкнутые контуры, совпадающие с "окнами", образуемыми элементами и назовем ячейками.
Положительное направление токов в ячейках можно выбрать произвольно, однако уравнения записываются проще, если все направления выбраны по часовой стрелке.
Введем для каждой ячейки некоторый гипотетический контурный ток. Протекая через элементы, этот ток создает падения напряжений. Алгебраическая сумма напряжений вдоль замкнутого контура должна быть равна нулю.
Для рассматриваемой схемы
СЛУ
Преобразовав уравнения, запишем в матричной форме
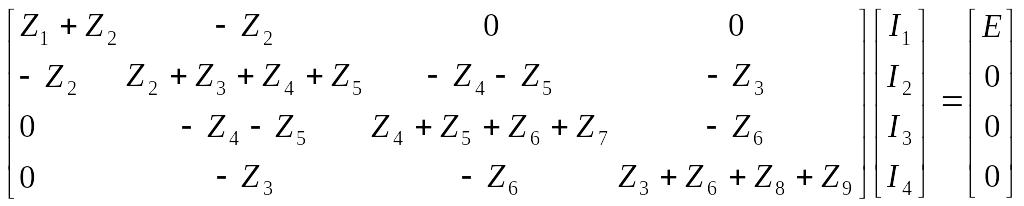
Правила составления ур-й в матр. Форме по схеме
Z·I=E.
Мы получили описание цепи в виде СЛУ. Решение этой системы линейных уравнений производится либо прямыми, либо итерационными методами.
В данном случае будем рассматривать только прямые методы решений.
Пусть имеется СЛУ
A·x=b.
А - матрица размером n×n с постоянными коэффициентами.
b - n-мерный вектор известных констант.
х - n-мерный вектор неизвестных.
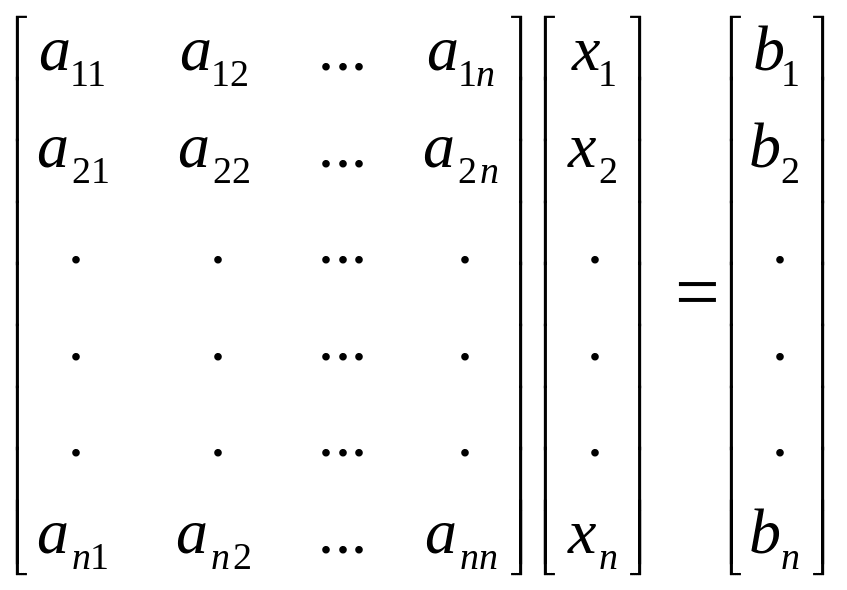
Формально эту систему уравнений можно решить, обратив матрицу А
X=A-1·b.
Очень часто, когда требуется найти только одну "выходную" переменную используется метод, называемый правилом Крамера.
Это правило гласит, что для системы A·x=b k-я компонента xk вектора х равна отношению определителя матрицы А, в которой k столбец заменен вектором b, и определителя матрицы А.
Правило Крамера используется для решения уравнений низкого порядка и требует больших затрат машинного времени и редко применяется в вычислительных программах.