Оглавление

Введение 3

1. Сравнительный анализ вероятностей катастрофы летательного аппарата 4

1.1. Вероятность катастрофы ЛА с дублирующими системами 6

1.1.1. Стуктура событий вероятности катастроф, связанных с отказом двигателей Е_KD 7

1.1.2. Структура событий вероятности катастроф, связанных с отказом систем энергоснабжения Е_КЭ 11

1.1.3. Структура событий вероятности катастроф, связанных с отказом вспомогательных подсистем Е_КС 12

1.2. Вероятность катастрофы ЛА без дублирующих систем 14

2. Определение надежности элементов системы энергоснабжения самолета 16

Выводы 21

Список использованных источников 22

Введение

1. Сравнительный анализ вероятностей катастрофы летательного аппарата

Рассмотрим летательный аппарат (ЛА), который состоит из: m двигателей с вероятностью отказа ; n дублирующих систем энергоснабжения с вероятностью отказа ; N вспомогательных подсистем с вероятностью отказа каждая (Таблица 1).

Таблица1

Данные ЛА

m	r	n	N	P1	P2	P3	PD	P1э	P2э	P3э	PС
3	1	3	103	8·10-4	2·10-4	4·10-4	0,6	5·10-4	4·10-4	10-3	8·10-8

Введем обозначения событий:

D₁, D₂, D₃ – отказ 1-го, 2-го и 3-го двигателей соответственно;

B₁, B₂, B₃ – отказ 1-й, 2-й и 3-й системы энергоснабжения соответственно;

C_i – отказ i-й вспомогательной подсистемы, i = ;

Е_К – катастрофа;

Е_KD, Е_KЭ, Е_KC – катастрофы, связанные с отказом двигателей, систем энергоснабжения и вспомогательных подсистем соответственно.

Катастрофа наступает, если выходят из строя: любые (r+1) и более двигателей; все системы энергоснабжения; хотя бы одна из N вспомогательных подсистем.

В случае отказа любого r из m двигателей катастрофа наступает с вероятностью .

Определим вероятность катастрофы ЛА и сравним ее с вероятностью катастрофы ЛА без дублирующих систем (один двигатель с вероятностью катастрофы , одна система энергоснабжения с вероятностью отказа и N вспомогательных подсистем с вероятностью отказа каждая), предполагая, что все упомянутые выше системы и подсистемы ЛА функционируют независимо друг от друга.

В обоих случаях сравним вероятности катастроф, связанных с отказом: двигателей; систем энергоснабжения; вспомогательных подсистем.

1. Вероятность катастрофы ла с дублирующими системами

Рассмотрим вероятность катастрофы ЛА с дублирующими системами:

. (1)

Перейдем к противоположным событиям и будем иметь:

. (2)

Преобразуем равенство (2) по закону де Моргана, получим:

. (3)

Вероятность катастрофы будет определяться по формуле:

(4)

Вследствие независимости событий из равенства (4) получим:

. (5)

Рассмотрим структуру событий Е_KD, Е_KЭ, Е_KC и найдем их вероятности катастроф, связанных с отказом: двигателей Е_KD; систем энергоснабжения Е_KЭ; вспомогательных подсистем Е_KC .

1.1.1. Стуктура событий вероятности катастроф, связанных с отказом двигателей еkd

Рассмотрим структуру событий Е_KD и найдем P(Е_KD) = P_KD

Событие Е_KD – это событие, состоящее в том, что катастрофа произошла из-за отказа двигателей, а по условию задачи катастрофа, связанная с отказом двигателей, наступает, если выходят из строя любые (r + 1) и более двигателей из m двигателей, а в случае отказа любого r из m двигателей катастрофа наступает с вероятностью P_D .

. (6)

В нашем случае число двигателей m = 3, а r = 2; тогда

r + 1 = 1 + 1 = 2. (7)

Подставив данные (7) в равенство (6) получим:

(8)

где – событие, состоящее в том, что катастрофа произошла из-за отказа любого r = 1 из m = 3 двигателей;

– событие, состоящее в том, что катастрофа произошла в связи с выходом из строя любых (r+1) = 2 и более двигателей:

,

.

Катастрофа, связанная с отказом r = 1 двигателя (при работающих остальных), не обязательно влечет за собой катастрофу (а с вероятностью P_D), значит,

тогда

Так как события и несовместны, тогда

Учитывая выражение (9), получим:

С другой стороны, катастрофа, связанная с отказом r = 1 двигателя (при работающих остальных) из трех имеющихся у ЛА по условию задачи, есть следующее событие:

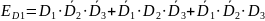, (11)

то есть работает только 1-й, либо 2-й, либо 3-й двигатель из трех имеющихся у ЛА.

По определению условной вероятности имеем:

Используя равенство (10) и несовместимость его слагаемых, получим:

Вследствие независимости всех событий и так как , будем далее иметь:

Так как

P (D_i) = P_i , i = 1,3 и P (E_K / E_D2) = P_D ,

тогда

Если выполняется условие

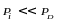(12)

для всех и учитывая, что значение вероятности случайного события меньше единицы, то

,

а также значит, что

Тогда имеем

. (13)

Подставив значения, данные из условия задания, получим:

.