1. Потери на вход в трубу

,

где – скорость во второй трубе. Коэффициент потерь на вход в трубу возьмем из таблицы 6. .

2. Потери на трение по длине в первой трубе:

.

Предположим, что режим течения – турбулентный.

Высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Коэффициент Шези по формуле Маннинга:

Определим через коэффициент Шези C.

.

Из таблицы 5 .

Тогда

. .

.

.

3. Потери на внезапное сужение

; .

Значение коэффициента потерь на внезапное сужение из таблицы 7, с применением линейной интерполяции

,

.

4. Потери на трение по длине во второй трубе

.

Положим, что режим течения – турбулентный.

Для новых стальных цельнотянутых труб высота выступов эквивалентной равномерной зернистой шероховатости равна

.

Предположим, что труба гидравлически шероховатая и определим через коэффициент Шези C

; б

Тогда:

.

5. Потери на внезапное расширение

6. Потери на трение по длине во третьей трубе

.

Определим значение числа Рейнольдса в третьей трубе

.

Предположим, что режим течения – турбулентный.

Определим через коэффициент Шези C

; б

Сумма всех потерь

Выразим значения скорости в первой и во второй трубах через значение скорости в третьей трубе

; .

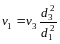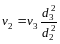Тогда сумма потерь примет вид

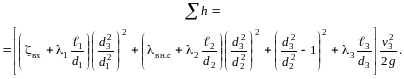
Уравнение Бернулли

запишем в виде

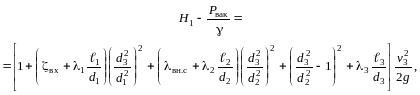
где

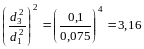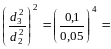, 16, .

Тогда значение скорости в третьей трубе вычисляется по формуле

Значение скорости трубах:

.

.

.

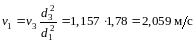Режимы течения в трубах

,

Для проверки действительного существования квадратичной области сопротивления вычислим числа Рейнольдса:

,

,

.

Так как

117882>37037,

176641>18518,

88320>37036,

то области сопротивления выбраны правильно.

Значения скоростного напора в трубах

Вычислим значения потерь

1. Потери на вход в трубу

.

2. Потери на трение по длине в первой трубе:

.

3. Потери на внезапное сужение

.

4. Потери на трение по длине во второй трубе

.

5. Потери на внезапное расширение

6. Потери на трение по длине во третьей трубе

.

Суммируем все потери:

Суммарный напор будет равен

,

что соответствует заданному значению

Построение линии полной удельной энергии

Значение удельной энергии равно т.е. равно кинетической энергии на выходе.

Построение пьезометрической линии(линии удельной потенциальной энергии)

Скоростные напоры:

, , .

Коэффициент Кориолиса принимаем равным .

В расчетных сечениях:

.

;

;

;

;

;

.

На выходе из трубопровода давление (избыточное) равно нулю, и конец пьезометрической линии совпадает с центром выходного сечения.