II подход

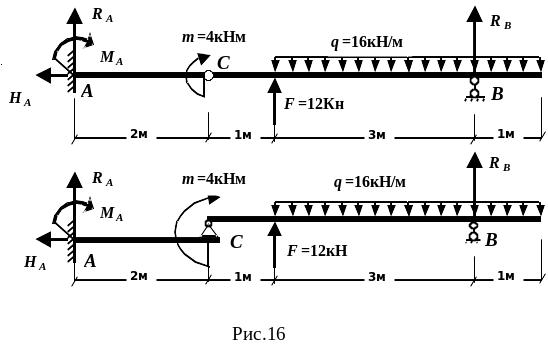
Расчет балки с промежуточным шарниром можно произвести путем составления поэтажной схемы (рис.16)

Для этого балка разрезается по промежуточному шарниру (шарнирам) и выделяются основная и подвесные балки.

Основной является та балка, которая может самостоятельно нести внешнюю нагрузку после разрезания по промежуточному шарниру (балка AC на рис.16).

Подвесная же балка не может работать самостоятельно вследствие недостаточности связей, закрепляющих ее от смещения как абсолютно твердого тела (балка CB на рис.16).

Расчет балок производят отдельно, начиная с подвесных балок. При последующем расчете основной балки, кроме заданных внешних нагрузок, к ней должны быть приложены реакции взаимодействия с подвесными балками.

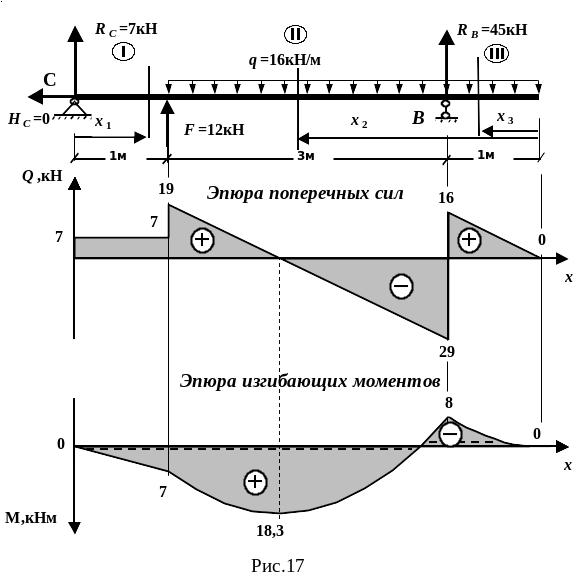
1.Определение опорных реакций и построение эпюр q и m подвесной балки cb (рис.17)

a) Определение опорных реакций

H_С=0; H_С=0.

F·1  q·4·3 + R_B·4=0;

12  16·4·3 + R_B·4=0;

 180 + R_B·4=0; R_B= кН;

R_C·4 – F·3 + q·4·1 =0;

 R_C·4 – 12·3 + 16·4·1 =0;

 R_C·4+28=0; R_C= кН.

Проверка правильности вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

R_C + F  q4 + R_B = 7 + 12  16·4 + 45=64  64=0.

б) Построение эпюр Q и M

I участок (начало отсчета на левом конце балки);

Q(x₁)= R_C = 7 кН;

M(x₁)= R_C x₁ = 7x₁;

M (0)= 0 (значение на левой границе участка);

M (2)= 7 кНм (значение на правой границе участка).

II участок (начало отсчета на правом конце балки);

Q(x₂)= – R_B + qx₂= – 45 + 16x₂;

Q(1)= – 45 + 16·1= – 29 кН (значение на правой границе участка);

Q(4)= – 45 + 16·4= 19 кН (значение на левой границе участка).

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:

Q(x₀)= – 45+16x₀=0; x₀=45/16=2,8125 м=2,81м;

M(x₂)= R_B(x₂ –1) – q /2= 45(x₂ –1) – 16 /2= 45(x₂ –1) – 8 ;

M (1) = 45(1 –1) – 8·1²= – 8 кНм (значение на правой границе участка);

M (2,81) = 45(2.81 –1) – 8·2,81²= 18,28 кНм=18,3 кНм;

M (4)= 45(4 –1) – 8·4 ² =7 кНм (значение на левой границе участка).

III участок (начало отсчета на правом конце балки)

Q(x₃)= qx₃ = 16x₃ ;

Q(0)= 0 (значение на правой границе участка);

Q(1)= 16 кН (значение на левой границе участка);

M (x₃)= – q /2 = – 16 /2= – 8 ;

M (0)=0 (значение на правой границе участка);

M (1)= – 8·1² = – 8 кНм (значение на левой границе участка).

Используя полученные результаты, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис. 17.

2.Построение эпюр q и m основной балки ac (рис.18)

Основная балка является консольной, поэтому определять опорные реакции R_A, M_A не обязательно. Их значения установим по эпюрам Q и M, используя правило скачков.

I участок (начало отсчета на правом конце балки);

Q(x)=R_C=7 кН;

M(x)= –m – R_C x = – 4 – 7x;

M(0)= – 4 кНм;

M(2)= – 18 кНм.

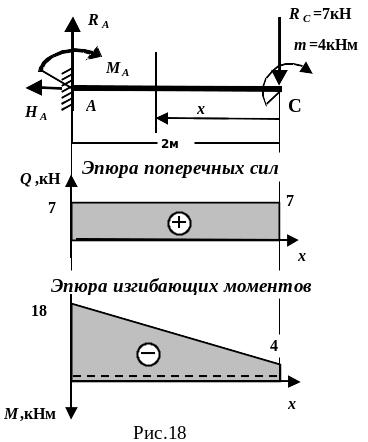По полученным значениям строим эпюры Q и M основной балки, как показано на рис.18.

Окончательный вид эпюр Q и M для заданной балки с промежуточным шарниром показан на рис.15.