Момент инерции поперечного сечения
609,7
см4 =
610 см4.
Определяем напряжение в точке 1 ( z1=zmax=D/2 )
МПа.
Определяем напряжение в точке 2 ( z2=d/2; d = 6,41 см = 6,41·10-2 м)
59,371
МПа =
= 59,4 МПа.
Напряжения в точках 3 и 4 будут равны
МПа,
101
МПа,
т.к. поперечное сечение симметрично относительно оси y.
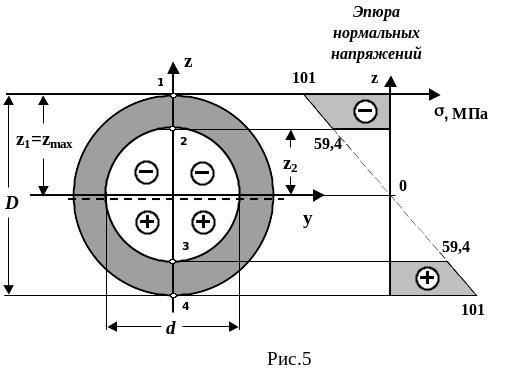Используя
полученные данные, строим эпюру нормальных
напряжений по высоте балки, которая
графически изображается наклонной
прямой линией (рис.5)
Опасными точками поперечного сечения называются точки, напряжения в которых достигают наибольших по величине значений.
В нашей задаче точки 1 и 4 – опасные по нормальным напряжениям. Обратите внимание, что они являются наиболее удаленными от нейтральной линии (ось y).
Задача 2. Расчет на прочность балки на двух опорах по методу предельных состояний
Исходные данные:
a=2 м; b=4 м; с=1 м; q=10 кН/м;
m=19 кНм; F=12 кН;
;
2,5.
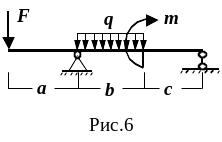
Д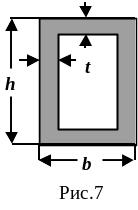
ля
заданной расчетной схемы балки на двух
опорах (рис.6) требуется:
1.Построить эпюры поперечных сил Q и изгибающих
моментов М;
2.Из условия прочности по методу предельных состоя-
ний подобрать размеры коробчатого сечения (рис. 7)
при
заданных отношениях
и
.
Принять
расчетное сопротивление R=210МПа, коэффициент перегрузки n=1,5; коэффициент условий работы γс=1. При определении геометрических характеристик сечения все размеры выразить через t.
3.Определить опасные сечения по нормальным и каса-
тельным напряжениям и для этих сечений построить:
а) эпюру нормальных напряжений по высоте балки;
б) эпюру касательных напряжений в пределах высоты стенки.
Решение
1. Определение опорных реакций
Для балки, изображенной на рис.8 составляем три уравнения статики:
;
.
F·2
q·4·2
– m
+ RB·5=0;
12·2 10·8 – 19 + RB·5=0;
75
+ RB·5=0;
RB=
15
кН.
F·7
RA·5
+ q·4·3
m=0;
12·7 RA·5 + 10·12 19 =0;
185
RA·5=0;
RA=
37
кН.
Проверяем правильность вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)
–
F+
RA
–
q·4
+ RB
= – 12 + 37 – 40 + 15 = 52 – 52=0.
2. Построение эпюр поперечной силы q и изгибающего момента m
Расчетная схема балки имеет три участка, которые пронумеруем слева направо (рис.8).
I
участок
(начало
отсчета на левом конце балки);
Q(x1)= – F= – 12 кН;
M(x1)= – Fx1= – 12x1;
M(0)=0 (значение на левой границе участка);
M(2)= – 12·2= – 24 кНм (значение на правой границе участка).
II
участок
(начало
отсчета на левой границе участка);
Q(x2)= – F + RA – qx2 = – 12 + 37 – 10x2 =25 – 10x2;
Q(0)=25 – 10·0= 25 кН (значение на левой границе участка);
Q(4)= 25 – 10·4= – 15 кН (значение на правой границе участка);
Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:
Q(x0)=25 – 10x0=0; x0=25/10=2,5 м;
M(x2)= – F ( x2+2) + RA x2 – q x22/2= – 12( x2+2) + 37x2 – 10x22/2=
= – 24 + 25x2 – 5x22;
M(0)= – 24 кНм (значение на левой границе участка);
M(2,5)= – 24 + 25·2,5 –5·2,52 = 7,25 кНм;
M(4)= – 24 + 25· 4 – 5·42= – 4 кНм (значение на правой границе участка).
III
участок
(начало отсчета на правом конце балки);
Q(x3)= – RB= – 15 кН;
M(x3)= RBx3 =15x3;
M(0)= 0 (значение на правой границе участка);
M(1)= 15 кНм (значение на левой границе участка).
Используя полученные значения, строим в масштабе эпюры поперечных сил и изгибающих моментов, как показано на рис.8.