
Глава II. Элементы векторной алгебры и аналитической геометрии.
ЗАНЯТИЕ 3.
ОПРЕДЕЛЕНИЯ И ДЕЙСТВИЯ С ВЕКТОРАМИ.
ПРЯМОУГОЛЬНАЯ
ДЕКАРТОВА СИСТЕМА КООРДИНАТ ВКЛЮЧАЕТ
В СЕБЯ ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ
ОСИ:ОСЬ АБСЦИСС
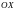 ,
ОСЬ ОРДИНАТ
,
ОСЬ ОРДИНАТ
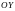 ,
ОСЬ АППЛИКАТ
,
ОСЬ АППЛИКАТ
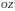 .
ОСИ ПЕРЕСЕКАЮТСЯ
В ОДНОЙ ТОЧКЕ
.
ОСИ ПЕРЕСЕКАЮТСЯ
В ОДНОЙ ТОЧКЕ
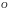 -НАЧАЛЕ
КООРДИНАТ.
-НАЧАЛЕ
КООРДИНАТ.
ОСИ
ОРИЕНТИРОВАНЫ ТАК, ЧТО ЕСЛИ СМОТРЕТЬ
ИЗ ПОЛОЖИТЕЛЬНОГО НАПРАВЛЕНИЯ ОСИ
НА
ПЛОСКОСТЬ
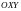 ,
ТО ОСИ
И
РАСПОЛАГАЮТСЯ
В ОБЫЧНОМ ПОРЯДКЕ.
,
ТО ОСИ
И
РАСПОЛАГАЮТСЯ
В ОБЫЧНОМ ПОРЯДКЕ.
ПУСТЬ
В ПРОСТРАНСТВЕ ЗАДАНА СИСТЕМА КООРДИНАТ
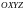 .
ЧТОБЫ ОПРЕДЕЛИТЬ
КООРДИНАТЫ ТОЧКИ
.
ЧТОБЫ ОПРЕДЕЛИТЬ
КООРДИНАТЫ ТОЧКИ 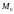 ,
ПРОВЕДЁМ ЧЕРЕЗ ЭТУ
ТОЧКУ ТРИ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ
ТРЁМ ОСЯМ КООРДИНАТ. ПУСТЬ ПЕРЕСЕЧЕНИЕ
ОДНОЙ ИЗ ПЛОСКОСТЕЙ С ОСЬЮ
ДАЁТ
ЧИСЛО
,
ПРОВЕДЁМ ЧЕРЕЗ ЭТУ
ТОЧКУ ТРИ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫЕ
ТРЁМ ОСЯМ КООРДИНАТ. ПУСТЬ ПЕРЕСЕЧЕНИЕ
ОДНОЙ ИЗ ПЛОСКОСТЕЙ С ОСЬЮ
ДАЁТ
ЧИСЛО
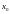 .
ПЕРЕСЕЧЕНИЕ ДРУГОЙ
ПЛОСКОСТИ С
ОСЬЮ
ДАЁТ
ЧИСЛО
.
ПЕРЕСЕЧЕНИЕ ДРУГОЙ
ПЛОСКОСТИ С
ОСЬЮ
ДАЁТ
ЧИСЛО
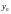 .
ПЕРЕСЕЧЕНИЕ ТРЕТЬЕЙ
ПЛОСКОСТИ С ОСЬЮ
ДАЁТ
ЧИСЛО
.
ПЕРЕСЕЧЕНИЕ ТРЕТЬЕЙ
ПЛОСКОСТИ С ОСЬЮ
ДАЁТ
ЧИСЛО
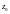 .
.
ПОЛУЧЕННАЯ
ТРОЙКА ЧИСЕЛ, ЗАПИСАННАЯ В ОПРЕДЕЛЁННОМ
ПОРЯДКЕ
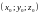 НАЗЫВАЕТСЯ
КООРДИНАТАМИ ТОЧКИ
.
НАЗЫВАЕТСЯ
КООРДИНАТАМИ ТОЧКИ
.
Геометрическая иллюстрация
ЕСЛИ НИ ОДНА ИЗ КООРДИНАТ ТОЧКИ НЕ РАВНА НУЛЮ
ТО ТРИ КООРДИНАТНЫХ ПЛОСКОСТИ И ТРИ ПЛОСКОСТИ,
ПРОВЕДЁННЫЕ ЧЕРЕЗ ТОЧКУ ПЕРПЕНДИКУЛЯРНО
КООРДИНАТНЫМ ОСЯМ ОБРАЗУЮТ ПАРАЛЛЕЛЕПИПЕД
ОДНА ИЗ ВЕРШИН КОТОРОГО ЛЕЖИТ В НАЧАЛЕ КООРДИНАТ
А ПРОТИВОПОЛОЖНАЯ ВЕРШИНА В ТОЧКЕ (РИС.3.1)
РИС.3.1
ЗАМЕЧАНИЕ.
КООРДИНАТЫ ТОЧЕК, ЛЕЖАЩИХ НА ОСЯХ
,
,
,
СООТВЕТСТВЕННО
РАВНЫ
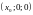 ,
,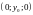 ,
,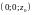 .
.
УПРАЖНЕНИЕ
3.1. НАЙТИ
КООРДИНАТЫ ВЕРШИН ПАРАЛЛЕЛЕПИПЕДА, У
КОТОРОГО ОДНА ИЗ ВЕРШИН ЛЕЖИТ В НАЧАЛЕ
КООРДИНАТ, А ПРОТИВОПОЛОЖНАЯ ВЕРШИНА
ИМЕЕТ
КООРДИНАТЫ
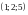 .
.
ЧАСТО, ЧТОБЫ ОТВЕТИТЬ НА ВОПРОС ИЗ ГЕОМЕТРИИ ИЛИ ФИЗИКИ НЕОБХОДИМО ЗАДАТЬ ОДНОВРЕМЕННО ЧИСЛО И НЕКОЕ НАПРАВЛЕНИЕ. НАПРИМЕР, ВОКЗАЛ НАХОДИТСЯ В ПЯТИ КИЛОМЕТРАХ В НАПРАВЛЕНИИ НА ЮГ. ИЛИ ШНУР НАТЯНУТ ВЕРТИКАЛЬНО ВНИЗ С СИЛОЙ 100 Н.
В ПОДОБНЫХ СИТУАЦИЯХ ОБЪЕДИНЯЮТ ЧИСЛО И НАПРАВЛЕНИЕ В ОДНО ПОНЯТИЕ-ВЕКТОР.
Векторная алгебра
ОПРЕДЕЛЕНИЕ
3.1 ВЕКТОР НА
ПЛОСКОСТИ ИЛИ В ПРОСТРАНСТВЕ ЭТО
НАПРАВЛЕННЫЙ ОТРЕЗОК. ОБОЗНАЧАЮТСЯ
ВЕКТОРЫ ТАК
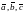 .
ЗАПИСЬ
.
ЗАПИСЬ
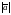 ОЗНАЧАЕТ ДЛИНУ ВЕКТОРА
ОЗНАЧАЕТ ДЛИНУ ВЕКТОРА
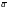 .
.
ОПРЕДЕЛЕНИЕ3.2
ВЕКТОР
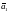 РАВЕН
ВЕКТОРУ
РАВЕН
ВЕКТОРУ
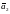 ,
ЕСЛИ ИХ МОЖНО
ПОЛНОСТЬЮ СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ
СДВИГОМ.
,
ЕСЛИ ИХ МОЖНО
ПОЛНОСТЬЮ СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ
СДВИГОМ.
ИЗ ОПРЕДЕЛЕНИЯ3.2 СЛЕДУЕТ, ЧТО ВЕКТОР НЕ ИЗМЕНЯЕТСЯ, ЕСЛИ ЕГО ПЕРЕМЕЩАТЬ ПАРАЛЛЕЛЬНО САМОМУ СЕБЕ.
ОПРЕДЕЛЕНИЕ
3.3 ВЕКТОР С
НАЧАЛОМ В ТОЧКЕ Р И КОНЦОМ В ТОЧКЕ Q
НАЗЫВАЮТ ВЕКТОРОМ СМЕЩЕНИЯ
И ОБОЗНАЧАЮТ
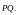 ДЛИНУ ВЕКТОРА
ДЛИНУ ВЕКТОРА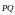 ОБОЗНАЧАЮТ
ОБОЗНАЧАЮТ
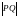 .
ЕСЛИ ТОЧКИ Р И Q СОВПАДАЮТ, ТО ТАКОЙ
ВЕКТОР НАЗЫВАЮТ НУЛЕВЫМ. НУЛЕВОЙ ВЕКТОР
НЕ ИМЕЕТ НАПРАВЛЕНИЯ И У НЕГО ДЛИНА
РАВНА НУЛЮ.
.
ЕСЛИ ТОЧКИ Р И Q СОВПАДАЮТ, ТО ТАКОЙ
ВЕКТОР НАЗЫВАЮТ НУЛЕВЫМ. НУЛЕВОЙ ВЕКТОР
НЕ ИМЕЕТ НАПРАВЛЕНИЯ И У НЕГО ДЛИНА
РАВНА НУЛЮ.
ОПРЕДЕЛЕНИЕ
3.4 ВЕКТОР,
ИМЕЮЩИЙ НАЧАЛО В НАЧАЛЕ КООРДИНАТ И
КОНЕЦ В ТОЧКЕ
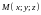 НАЗЫВАЕТСЯ
РАДИУСОМ-ВЕКТОРОМ ТОЧКИ
НАЗЫВАЕТСЯ
РАДИУСОМ-ВЕКТОРОМ ТОЧКИ
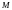 .
РАДИУС-ВЕКТОР ТОЧКИ
ОБОЗНАЧАЕТСЯ
.
РАДИУС-ВЕКТОР ТОЧКИ
ОБОЗНАЧАЕТСЯ
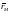 .
КООРДИНАТЫ ТОЧКИ
ЯВЛЯЮТСЯ ОДНОВРЕМЕННО КООРДИНАТАМИ
РАДИУСА-ВЕКТОРА .
.
КООРДИНАТЫ ТОЧКИ
ЯВЛЯЮТСЯ ОДНОВРЕМЕННО КООРДИНАТАМИ
РАДИУСА-ВЕКТОРА .
УГОЛ МЕЖДУ ВЕКТОРАМИ
ПАРАЛЛЕЛЬНЫМ
СДВИГОМ ПЕРЕМЕСТИМ ВЕКТОРЫ
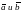 ТАК,
ЧТОБЫ НАЧАЛА ИХ СОВПАЛИ. ПОЛУЧЕННЫЙ
УГОЛ НАЗЫВАЕТСЯ
УГЛОМ МЕЖДУ ВЕКТОРАМИ. УГОЛ МОЖЕТ БЫТЬ
ЛИБО ОСТРЫЙ, ЛИБО ТУПОЙ. ВЕЛИЧИНА УГЛА
МЕЖДУ ВЕКТОРАМИ ВСЕГДА ПОЛОЖИТЕЛЬНА.
ТАК,
ЧТОБЫ НАЧАЛА ИХ СОВПАЛИ. ПОЛУЧЕННЫЙ
УГОЛ НАЗЫВАЕТСЯ
УГЛОМ МЕЖДУ ВЕКТОРАМИ. УГОЛ МОЖЕТ БЫТЬ
ЛИБО ОСТРЫЙ, ЛИБО ТУПОЙ. ВЕЛИЧИНА УГЛА
МЕЖДУ ВЕКТОРАМИ ВСЕГДА ПОЛОЖИТЕЛЬНА.
ОПРЕДЕЛЕНИЕ 3.5. ДВА ВЕКТОРА НАЗЫВАЮТСЯ КОЛЛИНЕАРНЫМИ ВЕКТОРАМИ, ЕСЛИ ПАРАЛЛЕЛЬНЫМ СДВИГОМ ИХ МОЖНО ПЕРЕМЕСТИТЬ НА ОДНУ ПРЯМУЮ.
ПРАВИЛО 3.1
УМНОЖЕНИЕ ЧИСЛА НА ВЕКТОР
ПРОИЗВЕДЕНИЕ
ЧИСЛА
 НА
ВЕКТОР
ЕСТЬ
НОВЫЙ ВЕКТОР
НА
ВЕКТОР
ЕСТЬ
НОВЫЙ ВЕКТОР
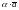 ДЛИНЫ
ДЛИНЫ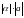 .
.
ВЕКТОР
ИМЕЕТ НАПРАВЛЕНИЕ, СОВПАДАЮЩЕЕ С
НАПРАВЛЕНИЕМ ВЕКТОРА
 ,
ЕСЛИ ЧИСЛО
,
ЕСЛИ ЧИСЛО
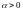 И НАПРАВЛЕНИЕ ПРОТИВОПОЛОЖНОЕ
НАПРАВЛЕНИЮ
,
ЕСЛИ ЧИСЛО
И НАПРАВЛЕНИЕ ПРОТИВОПОЛОЖНОЕ
НАПРАВЛЕНИЮ
,
ЕСЛИ ЧИСЛО
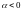 .
.
СЛОЖЕНИЕ ВЕКТОРОВ
ЕСЛИ
К КОНЦУ ВЕКТОРА
ПРИСОЕДИНИТЬ НАЧАЛО ВЕКТОРА ,
ТО ВЕКТОР
,
ИМЕЮЩИЙ НАЧАЛОМ НАЧАЛО
,
А КОНЦОМ КОНЕЦ ВЕКТОРА
И БУДЕТ НАЗЫВАТЬСЯ ВЕКТОРОМ СУММЫ
,
ТО ВЕКТОР
,
ИМЕЮЩИЙ НАЧАЛОМ НАЧАЛО
,
А КОНЦОМ КОНЕЦ ВЕКТОРА
И БУДЕТ НАЗЫВАТЬСЯ ВЕКТОРОМ СУММЫ
 .
.
ПРАВИЛО
3.1 ДВА ВЕКТОРА
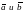 КОЛИНЕАРНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА
КОЛИНЕАРНЫ ТОГДА И ТОЛЬКО ТОГДА, КОГДА
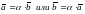 (3.1)
(3.1)
ОПРЕДЕЛЕНИЕ
3.6 ЛИНЕЙНОЙ
КОМБИНАЦИЕЙ ВЕКТОРОВ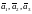 НАЗЫВАЮТ
ВЕКТОР
НАЗЫВАЮТ
ВЕКТОР
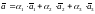 (3.2)
(3.2)
БАЗИСНЫЕ ЕДИНИЧНЫЕ ВЕКТОРА
ВЕКТОР
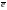 НАЗЫВАЮТ
ЕДИНИЧНЫМ, ЕСЛИ
ЕГО ДЛИНА РАВНА ЕДИНИЦЕ
НАЗЫВАЮТ
ЕДИНИЧНЫМ, ЕСЛИ
ЕГО ДЛИНА РАВНА ЕДИНИЦЕ 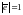 .
БАЗИСНЫМИ ВЕКТОРАМИ ЯВЛЯЮТСЯ :
ЕДИНИЧНЫЙ ВЕКТОР
.
БАЗИСНЫМИ ВЕКТОРАМИ ЯВЛЯЮТСЯ :
ЕДИНИЧНЫЙ ВЕКТОР
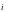 -НАПРАВЛЕННЫЙ
ПО ОСИ
-НАПРАВЛЕННЫЙ
ПО ОСИ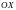 ,
ЕДИНИЧНЫЙ ВЕКТОР
,
ЕДИНИЧНЫЙ ВЕКТОР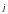 -НАПРАВЛЕННЫЙ
ПО ОСИ
-НАПРАВЛЕННЫЙ
ПО ОСИ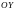 ,
ЕДИНИЧНЫЙ ВЕКТОР
,
ЕДИНИЧНЫЙ ВЕКТОР
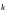 -НАПРАВЛЕННЫЙ
ПО ОСИ
-НАПРАВЛЕННЫЙ
ПО ОСИ
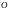
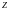 .
.
ЛЮБОЙ
ВЕКТОР
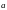 МОЖНО
ЗАПИСАТЬ ВВИДЕ ЛИНЕЙНОЙ КОМБИНАЦИИ
БАЗИСНЫХ ВЕКТОРОВ
МОЖНО
ЗАПИСАТЬ ВВИДЕ ЛИНЕЙНОЙ КОМБИНАЦИИ
БАЗИСНЫХ ВЕКТОРОВ
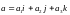 (3.3)
(3.3)
ЧИСЛА
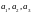 НАЗЫВАЮТСЯ КООРДИНАТАМИ ВЕКТОРА
.
НАЗЫВАЮТСЯ КООРДИНАТАМИ ВЕКТОРА
.
ЗАПИСИ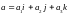 И
И
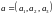 ОБОЗНАЧАЮТ ОДНО И ТО ЖЕ.
ОБОЗНАЧАЮТ ОДНО И ТО ЖЕ.
ЗАМЕЧАНИЕ. У КОЛЛИНЕАРНЫХ ВЕКТОРОВ КООРДИНАТЫ ПРОПОРЦИОНАЛЬНЫ.
КООРДИНАТНАЯ ЗАПИСЬ ПРАВИЛА 3.1
1)
ПРОИЗВЕДЕНИЕ ЧИСЛА
НА ВЕКТОР
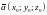 ,
ЗАДАННЫЙ КООРДИНАТАМИ, ВЫЧИСЛЯЕТСЯ ПО
ФОРМУЛЕ:
,
ЗАДАННЫЙ КООРДИНАТАМИ, ВЫЧИСЛЯЕТСЯ ПО
ФОРМУЛЕ:
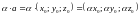 (3.4)
(3.4)
2) СУММА ДВУХ ВЕКТОРОВ, ЗАДАННЫХ КООРДИНАТАМИ, ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:
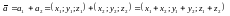 (3.5)
(3.5)
3) ДЛИНА
ВЕКТОРА
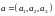 ВЫЧИСЛЯЕТСЯ
ПО ФОРМУЛЕ
ВЫЧИСЛЯЕТСЯ
ПО ФОРМУЛЕ
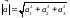 (3.6)
(3.6)
ПРИМЕР
3.1 ДАНЫ ДВА
ВЕКТОРА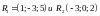 .
ВЫЧИСЛИТЬ ЛИНЕЙНУЮ КОМБИНАЦИЮ ВЕКТОРОВ
.
ВЫЧИСЛИТЬ ЛИНЕЙНУЮ КОМБИНАЦИЮ ВЕКТОРОВ
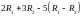 .
.
РЕШЕНИЕ.
ВЫЧИСЛИМ ВНАЧАЛЕ ВЕКТОР
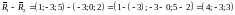 .
.
ДАЛЕЕ ЗАПИШЕМ УСЛОВИЕ ЗАДАЧИ В КООРДИНАТАХ
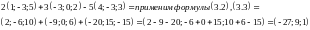
ПРИМЕР
3.2 ПУСТЬ
ДАНЫ ДВЕ ТОЧКИ
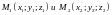 .
ВЫЧИСЛИТЬ КООРДИНАТЫ
.
ВЫЧИСЛИТЬ КООРДИНАТЫ
ВЕКТОРА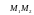 .
.
РЕШЕНИЕ.
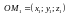 ,
,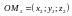 .
ДАЛЕЕ
.
ДАЛЕЕ 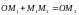
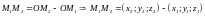 =
= 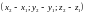 .
.
ЗАМЕЧАНИЕ. ЧТОБЫ ПОЛУЧИТЬ КООРДИНАТЫ ВЕКТОРА СМЕЩЕНИЯ НУЖНО ИЗ КООРДИНАТ КОНЦА ВЕКТОРА ВЫЧЕСТЬ КООРДИНАТЫ НАЧАЛА ВЕКТОРА.
