Полярная система координат.

Кроме декартовой системы координат для определения положения точек на плоскости часто используют полярную систему координат.

rrr

Определение 2.7. Полярные координаты точки это

упорядоченная пара чисел . это расстояние от

r

М

фиксированной точки ( называемой полюсом) до

∝

точки . угол(выраженный в радианах) между

О

между горизонтальной осью и отрезком рис.14.

рис.14

Если на плоскости введены одновременно две системы координат декартова система и полярная система, то между ними существует связь рис.15.

А

Y

X

r

∝

В

Рис.15

Из (рис.15.) следуют формулы связи

, (2.23)

И наоборот

(2.24)

Пример 2.9. Изобразить точку на координатной плоскости.

Решение. Сначала нужно поинтересоваться, в каких координатах задана данная точка.

Если в декартовых координатах, то рисунок будет таким (рис.16), если в полярных, то таким (рис.17)

115°

r=3

М

М

Рис.16 рис.17

Упражнение. Изобразить точки заданные в полярной системе координат

и найти прямоугольные координаты этих точек.

Изобразить точки заданные в декартовой системе координат:

и найти полярные координаты этих точек.

Если полярный радиус и полярный угол связаны друг с другом формулой ,

то при изменении угла будет изменяться и полярный радиус и точки опишут некоторую кривую.

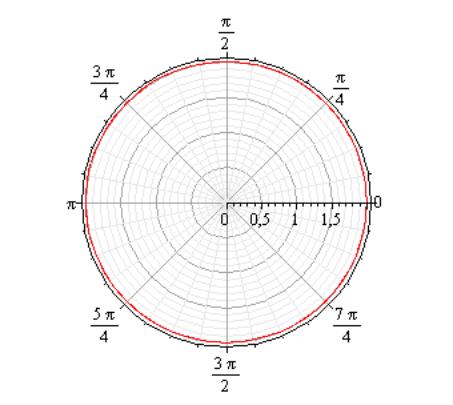
Пример 2.10. Построим кривые: 1) в декартовой системе координат;

2) в полярной системе координат.

Эскизы кривых приведены ниже

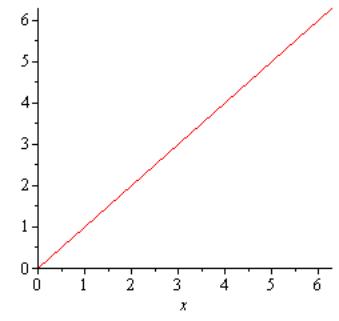
Пример 2.11. Построить по точкам кривые: 1) в декартовой системе координат;

2) в полярной системе координат.

Эскизы кривых приведены ниже

Упражнения.

Парабола.

Упражнение 2.1. Написать уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси ОХ и её параметр равен 3.

Упражнение 2.2. Определить величину параметра и дать эскизы парабол

Упражнение 2.3. Написать уравнение параболы, которая имеет фокус и вершину в начале координат.

Упражнение 2.4. Найти фокус и директрису параболы .

Упражнение 2.5. Написать уравнение параболы, у которой фокус и уравнение директрисы .

Окружность

Упражнение 2.6. Написать уравнение окружности, зная

1. её центр О и радиус ; 2) её центр О и радиус ;

Упражнение 2.7. Написать канонические уравнение эллипса, фокусы которого лежат на оси

абсцисс симметрично относительно начала координат, зная, что

1. его полуоси равны ;

2. его большая полуось равна 5, а расстояние между фокусами ;

3. расстояние между его фокусами , а эксцентриситет ;

4. расстояние между его директрисами равно 5 и расстояние между

фокусами .

Упражнение 2.8. Написать канонические уравнение эллипса, фокусы которого лежат на оси

ординат симметрично относительно начала координат, зная, что

1. его полуоси равны ;

2. его большая полуось равна 10, а расстояние между фокусами ;

3. расстояние между его фокусами , а эксцентриситет ;

4. расстояние между его директрисами равно и расстояние между

фокусами ;

Упражнение 2.9. Дан эллипс . Найти его

1. полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.

Упражнение 2.10. Определить тип кривой и дать эскиз её графика

1) ; 2)