Глава II. Элементы векторной алгебры и аналитической геометрии.

Занятие 2.

Кривые второго порядка.

ПАРАБОЛЫ.

ОПРЕДЕЛЕНИЕ 2.1 ПАРАБОЛА-ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЁННЫХ ОТ ЗАДАННОЙ ПРЯМОЙ И ФИКСИРОВАННОЙ ТОЧКИ НА ПЛОСКОСТИ (ТОЧКА НЕ ЛЕЖИТ НА ЗАДАННОЙ ПРЯМОЙ).

ПРЯМАЯ НАЗЫВАЕТСЯ ДИРЕКТРИСОЙ, А ТОЧКА ФОКУСОМ ПАРАБОЛЫ (РИС.1). ПРЯМАЯ, ПРОХОДЯЩАЯ ЧЕРЕЗ ФОКУС И ПЕРПЕНДИКУЛЯРНАЯ ДИРЕКТРИСЕ НАЗЫВАЕТСЯ ОСЬЮ СИММЕТРИИ ПАРАБОЛЫ. ТОЧКА ПЕРЕСЕЧЕНИЯ ПАРАБОЛЫ С ОСЬЮ СИММЕТРИИ НАЗЫВАЕТСЯ ВЕРШИНОЙ ПАРАБОЛЫ.

ПРИМЕР 2.1 НАПИСАТЬ УРАВНЕНИЕ ПАРАБОЛЫ, КОТОРАЯ ИМЕЕТ ФОКУС (-1,0) И УРАВНЕНИЕ ДИРЕКТРИСЫ Х=1.

РЕШЕНИЕ. ПУСТЬ ТОЧКА С КООРДИНАТАМИ М (х,у) ЛЕЖИТ НА ПАРАБОЛЕ . ТОГДА ПО ОПРЕДЕЛЕНИЮ 4.1 РАССТОЯНИЕ ОТ ТОЧКИ М ДО ФОКУСА РАВНО РАССТОЯНИЮ ОТ ТОЧКИ М ДО ДИРЕКТРИСЫ:

ВОЗВОДЯ ОБЕ ЧАСТИ В КВАДРАТ, ПОЛУЧАЕМ (рис.1)

.

рис.1 ИЛИ

ПОЛУЧЕННОЕ УРАВНЕНИЕ ЯВЛЯЕТСЯ КАНОНИЧЕСКИМ УРАВНЕНИЕМ ПАРАБОЛЫ.

ТЕОРЕМА 2.1 ПАРАБОЛА НА ХУ ПЛОСКОСТИ ИМЕЮЩАЯ:

1)ВЕРШИНУ В НАЧАЛЕ КООРДИНАТ; 2)ФОКУС НА ОСИ ОУ; 3) ДИРЕКТРИСУ

ИМЕЕТ УРАВНЕНИЕ (2.1)

ЭСКИЗ ПАРАБОЛЫ ПРЕДСТАВЛЕН НА РИС.2

РИС. 2

УПРАЖНЕНИЕ 2.1. НАЙТИ ПО ГРАФИКУ (рис.2) ФОКУС И ДИРЕКТРИСУ ПАРАБОЛЫ.

ТЕОРЕМА 2.2 ПАРАБОЛА НА ОХУ ПЛОСКОСТИ ИМЕЮЩАЯ:

1)ВЕРШИНУ В НАЧАЛЕ КООРДИНАТ; 2)ФОКУС НА ОСИ ОХ; 3) ДИРЕКТРИСУ ИМЕЕТ УРАВНЕНИЕ

(2.2)

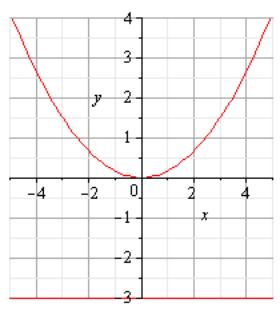
ЭСКИЗ ПАРАБОЛЫ ПРЕДСТАВЛЕН НА РИС.3.

РИС.3

УПРАЖНЕНИЕ 2.2 . НАЙТИ ПО ГРАФИКУ (рис.3) ФОКУС И ДИРЕКТРИСУ ПАРАБОЛЫ

Параллельный сдвиг координатных осей

ДОПУСТИМ, ЧТО ПАРАБОЛА ИМЕЕТ ГОРИЗОНТАЛЬНУЮ ЛИБО ВЕРТИКАЛЬНУЮ ОСЬ СИММЕТРИИ, НО ЕЁ ВЕРШИНА НЕ ЛЕЖИТ В НАЧАЛЕ КООРДИНАТ. МЫ ОПРЕДЕЛИМ ФОКУС И ДИРЕКТРИСУ ПАРАБОЛЫ ИЗ ЕЁ УРАВНЕНИЯ ВВОДЯ ВСПОМОГАТЕЛЬНЫЕ ОСИ КООРДИНАТ ПАРАЛЛЕЛЬНЫЕ ПЕРВОНАЧАЛЬНЫМ ОСЯМ И ВЫБИРАЯ ВЕРШИНУ ПАРАБОЛЫ В ТОЧКЕ .

ЕСЛИ НАЧАЛО КООРДИНАТ НОВОЙ СИСТЕМЫ ИМЕЕТ КООРДИНАТЫ В ПЕРВОНАЧАЛЬНОЙ СИСТЕМЕ , ТОГДА НОВЫЕ И СТАРЫЕ КООРДИНАТЫ СВЯЗАНЫ МЕЖДУ СОБОЙ УРАВНЕНИЯМИ

(2.3)

ПРИМЕР 2.2 НАЙТИ ФОКУС, ВЕРШИНУ И ДИРЕКТРИСУ ПАРАБОЛЫ

РЕШЕНИЕ. ВЫДЕЛЯЕМ ПОЛНЫЙ КВАДРАТ ПО ПЕРЕМЕННОЙ : ОТСЮДА . В ПОЛУЧЕННОМ УРАВНЕНИИ ПОЛОЖИМ

ТОГДА В НОВЫХ КООРДИНАТАХ УРАВНЕНИЕ ПРИНИМАЕТ ВИД

(2.4)

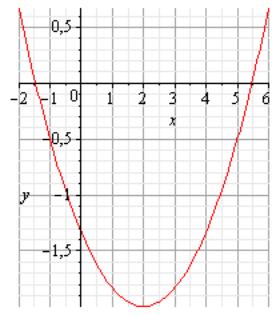
Рис.4

УПРАЖНЕНИЕ 2.3 НАЙТИ ПО ГРАФИКУ (рис.4) И ФОРМУЛЕ(2.4) ФОКУС И ДИРЕКТРИСУ ПАРАБОЛЫ В

СТАРЫХ И НОВЫХ КООРДИНАТАХ .

РЕШЕНИЕ. МЫ ИСПОЛЬЗОВАЛИ НОВУЮ СИСТЕМУ КООРДИНАТ В КОТОРОЙ НАЧАЛО НАХОДИТСЯ В ТОЧКЕ (2,-2). ПОЛУЧЕННОЕ УРАВНЕНИЕ (2.4) ИМЕЕТ ВИД

С . ФОКУС ПАРАБОЛЫ В НОВЫХ КООРДИНАТАХ , В СТАРЫХ КООРДИНАТАХ ЭТО БУДЕТ

. УРАВНЕНИЕ ДИРЕКТРИСЫ В НОВЫХ КООРДИНАТАХ В СТАРЫХ КООРДИНАТАХ .

ОКРУЖНОСТЬ.

ОПРЕДЕЛЕНИЕ 2.2. ОКРУЖНОСТЬ ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК РАВНОУДАЛЁННЫХ ОТ ФИКСИРОВАНОЙ

ТОЧКИ НАЗЫВАЕМОЙ ЦЕНТРОМ.

УРАВНЕНИЕ ОКРУЖНОСТИ С ЦЕНТРОМ В ТОЧКЕ 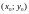И РАДИУСА ХОРОШО ИЗВЕСТНО

(2.5)

УПРАЖНЕНИЕ 4.4. ИСПОЛЬЗУЯ ГРАФИК, НАЙТИ КООРДИНАТЫ ЦЕНТРА ОКРУЖНОСТИ И ЕЁ РАДИУС (рис.5)

Рис.5

ЭЛЛИПС

ОПРЕДЕЛЕНИЕ 2.3. ЭЛЛИПС-ЭТО ГЕОМЕТРИЧЕСКОЕ МЕСТО ТОЧЕК НА ПЛОСКОСТИ ТАКИХ, ЧТО

СУММА РАССТОЯНИЙ ИХ ДО ДВУХ ФИКСИРОВАННЫХ ТОЧЕК ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.

ТОЧКИ НАЗЫВАЮТСЯ ФОКУСАМИ ЭЛЛИПСА.

МЫ БУДЕМ РАССМАТРИВАТЬ КАНОНИЧЕСКУЮ СИСТЕМУ КООРДИНАТ, В КОТОРОЙ НАЧАЛО КООРДИНАТ ЯВЛЯЕТСЯ ЦЕНТРОМ СИММЕТРИИ ЭЛЛИПСА. КРОМЕ ТОГО ЭЛЛИПС СИММЕТРИЧЕН ОТНОСИТЕЛЬНО ОСЕЙ ТАКИХ КООРДИНАТ.

ПРИМЕР 2.3. НАЙТИ УРАВНЕНИЕ ГЕОМЕТРИЧЕСКОГО МЕСТА ТОЧЕК ПЛОСКОСТИ С КООРДИНАТАМИ ДЛЯ КОТОРЫХ СУММА РАССТОЯНИЙ ДО ДВУХ ТОЧЕК РАВНА 4.

РЕШЕНИЕ. СОГЛАСНО ОПРЕДЕЛЕНИЮ 2.3. ИМЕЕМ:

УРАВНЕНИЕ ЯВЛЯЕТСЯ УРАВНЕНИЕМ ЭЛЛИПСА В КАНОНИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ.

ОБЩИЙ СЛУЧАЙ СФОРМУЛИРОВАН В СЛЕДУЮЩЕЙ ТЕОРЕМЕ 2.3.