91

Моделирование временных рядов данных 79

Временные ряды данных: характеристики и общие понятия 79

Временной ряд, уровень временного ряда; классификация факторов, формирующих уровень ряда 79

Выявление структуры временного ряда 80

Алгоритм расчета коэффициента автокорреляции 81

Коррелограмма 82

Определение структуры временного ряда на основании автокорреляционной функции и коррелограммы 82

Аддитивная и мультипликативная модели временных рядов 83

Компоненты временного ряда 83

Методы выравнивания уровней временного ряда 83

Выравнивание на основе скользящей средней 84

Алгоритм построения модели временного ряда на примере аддитивной и мультипликативной моделей 86

Модели стационарных и нестационарных временных рядов и их идентификация 87

Идентификация временных рядов в направлении определения их стационарности 89

Моделирование временных рядов данных Временные ряды данных: характеристики и общие понятия Временной ряд, уровень временного ряда; классификация факторов, формирующих уровень ряда

Временной (динамический) ряд – упорядоченный во времени набор значений некоторого показателя. Он может быть условно представлен в виде суммы четырех составляющих:

y

(5.1)

_t = u_t + v_t + c_t + _t,

где y_t - значение показателя в момент времени t, или уровень ряда;

u_t - тренд,

v_t – сезонная компонента процесса;

c_t – циклическая компонента процесса;

_t - случайная компонента.

Из перечисленных факторов, формирующих уровень временного ряда, первые три являются закономерными.

Тренд представляет собой детерминированную (неслучайную) компоненту процесса, которая характеризует основную тенденцию исследуемого явления, обусловленную влиянием долговременных факторов (например, экономический рост, НТП и др.).

Сезонная компонента отражает в модели влияние сезонных факторов, которые также влияют на экономические процессы (например, сезонные колебания спроса на некоторые товары). Сюда же относят и те факторы, которые повторяются с более короткой цикличностью (ежемесячно, еженедельно – например, колебания пригородных пассажироперевозок по дням недели).

Циклическая (конъюнктурная) компонента отражает факторы, которые повторяются через достаточно длительные промежутки времени (например, демографические спады, экономические подъемы и кризисы).

Случайная компонента представляет собой случайный остаток и имеет тот же смысл, что и в ранее изученных регрессионных моделях.

Разложить ряд на эти четыре составляющие непосредственно нельзя, но можно в процессе его изучения постараться выделить каждую из них. При этом наиболее важной задачей изучения временных рядов обычно считают выявление тренда, позволяющего построить как можно более достоверный экономический прогноз.

В соответствии с (5.1) все факторы, формирующие уровень ряда, можно классифицировать на три основные группы:

1) долговременные факторы, определяющие тренд (основную тенденцию) временного ряда;

2) факторы, связанные с циклическими колебаниями (их действие повторяется с разной по длительности периодичностью – каждую неделю, месяц, квартал, через несколько лет);

3) случайные факторы (связанные со стохастической, вероятностной природой временного ряда).

Выявление структуры временного ряда

Автокорреляция уровней временного ряда - это корреляционная зависимость между их последовательными значениями.

Алгоритм расчета коэффициента автокорреляции

Для измерения тесноты автокорреляционной зависимости рассчитывают коэффициент автокорреляции.

Рассмотрим два набора уровней временного ряда, отстоящих друг от друга на один временной промежуток: y₂, y₃, …, y_n и y₁, y₂, …, y_n-1. Для оценки тесноты линейной связи между ними воспользуемся формулой для расчета коэффициента парной корреляции (1.5), подставив в нее эти значения показателя:

(5.2)

где

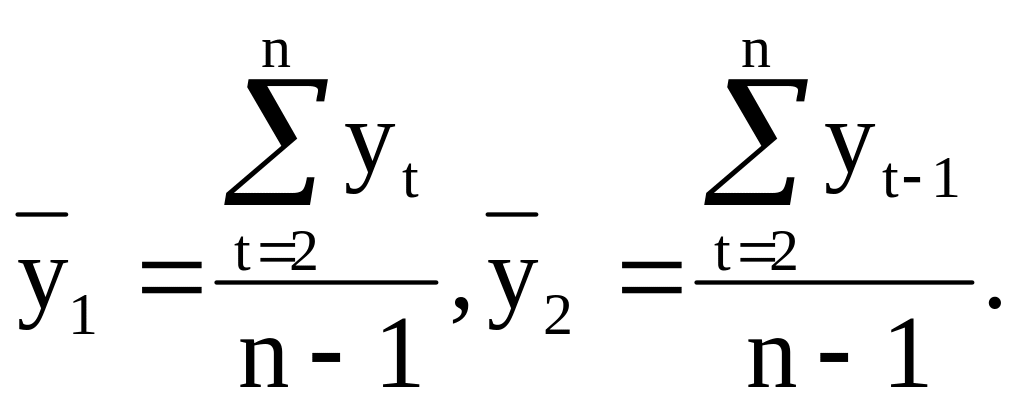
Для расчета того же самого коэффициента можно также воспользоваться и другими рабочими формулами, например, формулой (3.8):

(5.3)

Поскольку уровни временного ряда здесь «сдвинуты» на один промежуток времени (т.е. лаг составляет единицу), коэффициент автокорреляции, рассчитанный по формулам (5.2) или (5.3), называют коэффициентом автокорреляции первого порядка.

Взяв уровни временного ряда, отстоящие друг от друга на два промежутка: y₃, y₄, …, y_n и y₁, y₂, …, y_n-2, - можно рассчитать коэффициент автокорреляции второго порядка. Аналогично могут быть рассчитаны коэффициенты более высоких порядком.

Промежуток времени, на который отстоят друг от друга два фрагмента временного ряда, называется лагом. Для коэффициентов автокорреляции первого порядка лаг составляет единицу, второго порядка – два и т.д.

Коэффициент автокорреляции порядка τ можно рассчитать по формуле:

(5.4)

где

τ – лаг.