Обобщенный мнк

Рассмотрим отдельно две важные предпосылки МНК: гомоскедастичность и отсутствие автокорреляции остатков. Взяв n наблюдений, для каждого из них можно получить регрессионный остаток ε₁, ε₂, …, ε_n. Каждый из этих остатков сам по себе является случайной величиной. Для этих случайных величин можно построить ковариационную матрицу, на диагонали которой будут стоять дисперсии остатков, а остальные элементы будут представлять собой ковариации между ними (матрица симметрична относительно главной диагонали):

(2.15)

Если остатки гомоскедастичны, то элементы на главной диагонали этой матрицы будут равны между собой. Если автокорреляция остатков отсутствует, то ненулевые элементы этой матрицы могут стоять только на главной диагонали. Существенное отличие любого другого элемента матрицы (2.15) от нуля означает, что регрессионные остатки коррелируют.

Как уже было сказано, гетероскедастичность и автокорреляция остатков приводят к тому, что оценки, полученные МНК, будут неэффективными. Исключить то и другое можно с помощью модификации МНК – обобщенного метода наименьших квадратов (ОМНК), суть которого сводится к тому, что при нахождении вектора параметров А используют не формулу (2.10), а следующую формулу:

А

(2.16)

= (X^ТΩ^-1X)^-1X^ТΩ^-1Y,

где Ω^-1 – матрица, обратная ковариационной матрице Ω.

Можно доказать, что при использовании этой формулы оценки будут обладать свойством эффективности (теорема Айткена). Доказательство можно найти, например, в [Яновский Л.П., Буховец А.Г. Введение в эконометрику: уч. пособие – 2-е изд., доп. – М.: Кнорус, 2007. – 256 с.].

Исключение гетероскедастичности с помощью омнк

Предположим, что выполняется требование равенства математического ожидания регрессионного остатка нулю. Тогда дисперсия регрессионных остатков равна просто ожидаемому квадрату остатка: σ²(ε) = M(ε – M(ε))² = M(ε²); σ²(ε_i) = M(ε_i²).

Предположим, что требование отсутствия автокорреляции остатков тоже выполняется. Тогда ковариационная матрица остатков (2.15) примет вид диагональной матрицы (ненулевые элементы стоят только на главной диагонали):

(2.17)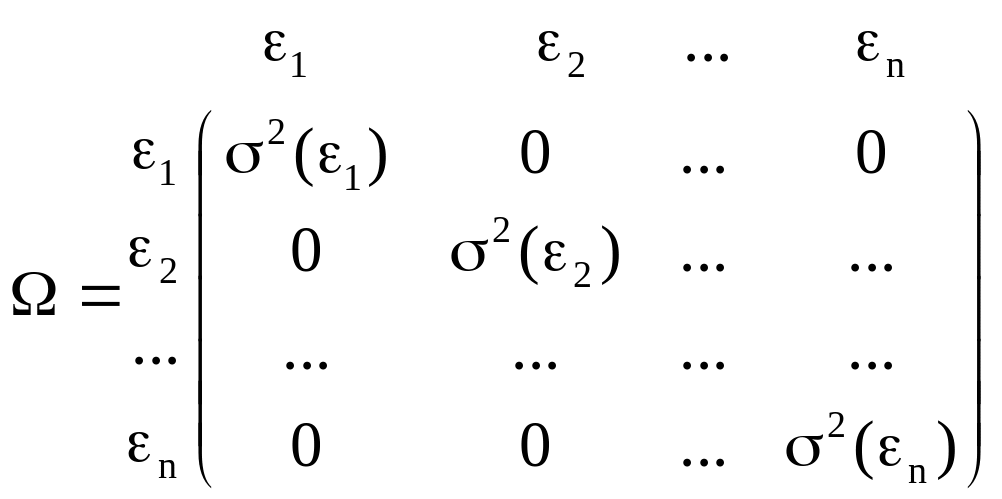

Пусть остатки гетероскедастичны, т.е. элементы на главной диагонали матрицы (2.17) не равны между собой. Применение ОМНК по формуле (2.16) с такой ковариационной матрицей сведется к тому, что в каждом i–м наблюдении все значения переменных будут поделены на одно и то же число σ²(ε_i). Такая модификация ОМНК называется взвешенным МНК.

Однако в реальных экономических задачах дисперсии регрессионных остатков для отдельных наблюдений неизвестны, и нет возможности построить ни матрицу (2.15), ни матрицу (2.16). Поэтому вместо этих матриц обычно используют какую-либо их оценку.

Для определения коэффициентов при использовании взвешенного МНК может быть использован следующий подход. Предположим, что дисперсии остатков σ²(ε_i) пропорциональны величине σ²(ε) (дисперсии генеральной совокупности значений случайной компоненты). Коэффициенты пропорциональности обозначим К_i, - эти коэффициенты характеризуют неоднородность дисперсии (способ их нахождения обсудим позже). Получим для каждого из n наблюдений:

σ

(2.18)

²(ε_i) = σ²(ε) * К_i

В основе применения МНК к линеаризованной функции лежит соотношение (2.1) (на примере парной линейной регрессии), которое может быть представлено следующим образом: . Если в левой части этого выражения каждое слагаемое в скобках разделить на , то в результате каждое слагаемое в правой части будет скорректировано на величину К_i. Поскольку из формулы (2.19) σ²(ε_i)/К_i = σ²(ε), можно условно считать, что после такого преобразования данные будут гомоскедастичны, т.е. иметь общую дисперсию σ²(ε).

Итак, чтобы применить к парной линейной регрессии ОМНК в случае гетероскедастичности остатков, необходимо обе части уравнения y = ax + b разделить на для всех наблюдений:

(2.19)

Чтобы это сделать, исходные данные модели – значения x_i и y_i, делят на . Одновременно осуществляют замену переменных

(2.20)

Значения новых переменных γ и α представляют собой значения показателей, взвешенные на коэффициенты . В общем случае эти веса надо задать для каждого наблюдения (каждой пары γ_i и α_i).

После такой замены уравнение регрессии примет вид

(2.21)

Полученное выражение представляет собой уравнение множественной (двухфакторной) линейной регрессии, в которой результативный признак обозначен γ, а признаки-факторы - α и β. Параметры регрессии a и b можно найти из системы нормальных уравнений (2.3). В данном случае первое уравнение в системе (2.3) следует опустить, так как свободный член регрессии (2.21) равен нулю (здесь оба параметра - a и b - представляют собой коэффициенты при переменных). Система примет вид:

(2.22)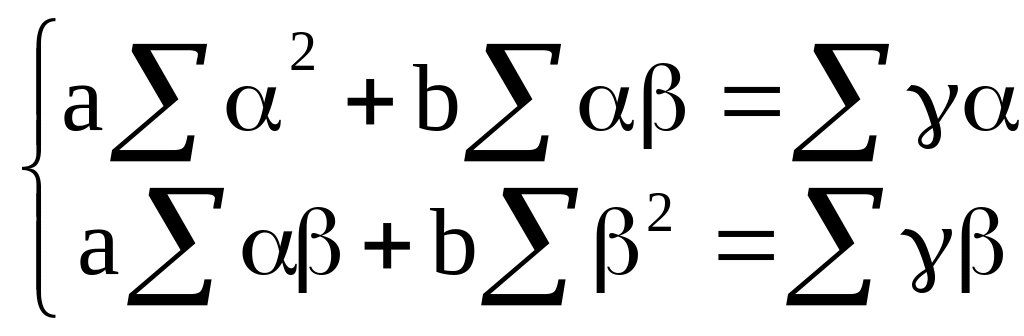

где

Каким образом определяются коэффициенты К_i? Существуют различные подходы к их определению, и выбор любого из них неизбежно влияет на значение полученных параметров модели.

Иногда предполагают, что этими коэффициентами являются сами значения фактора. В многофакторной модели при этом одновременно встает проблема выбора одного из факторов (того, значения которого будут использованы при расчете весов). Например, можно взять последний по порядку фактор в множественной регрессии.

Следует отметить, что при этом, чем меньше значение фактора, тем на меньшую величину будет поделена величина дисперсии, т.е. весовой коэффициент будет больше. Тем самым повышаются веса дисперсий ошибок в наблюдениях с меньшими значениями. Это говорит о том, что предположение о пропорциональности между коэффициентами К_i и значениями фактора может быть вполне обосновано с экономической точки зрения: большим значениям фактора действительно может соответствовать большая дисперсия, которую необходимо умножить на меньший вес, чтобы добиться гомоскедастичности.