Свойства оценок, получаемых при помощи мнк

Понятно, что при многократном проведении наблюдений в результате расчетов будут получены различные значения параметров (в результате случайных колебаний). Например, если мы определяем параметры парной линейной регрессии a и b, то в результате исследования одной выборки мы получим значения параметров a₁ и b₁, по другой выборке - a₂ и b₂, и т.д. можем получить бесконечно много оценок параметров. Таким образом, сами оценки представляют собой случайную величину, для которой можно рассчитать вероятностные характеристики.

Математическое ожидание и дисперсия. В теории вероятностей среднее значение случайной величины, полученное при неограниченно большом числе опытов, называют ее математическим ожиданием и обозначают М(x) (x – случайная величина).

Математическое ожидание квадрата отклонения случайной величины от своего математического ожидания называют дисперсией (соответствует понятию дисперсии в статистике – средний квадрат отклонений от среднего) и обозначают D(x) или . Для расчета дисперсии удобно использовать не ее определение D(x) = M(x – M(x))², а следующую формулу: D(x) = M(x²) - – M²(x)). Иными словами, дисперсию можно рассчитать, как разность между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания¹.

Итак, выборочные оценки параметров имеют математическое ожидание и дисперсию.

Если бы мы могли охватить в исследовании не выборку, а всю генеральную совокупность данных, то получили бы значения параметров регрессии, которые условно можно назвать истинными.

Оценки параметров, полученные МНК, обладают важными свойствами, строгое доказательство которых приводится в математической статистике (здесь не рассматривается):

1) несмещенность;

2) состоятельность;

3) эффективность.

Рассмотрим их подробно.

Несмещенность. Свойство несмещенности заключается в том, что математическое ожидание оценки равно неизвестному истинному значению параметра. Это означает, что выборочные оценки как бы концентрируются вокруг неизвестных истинных значений параметров. Это очень важное свойство, - если бы оно не выполнялось, метод давал бы заведомо неверную информацию.

Состоятельность. Свойство состоятельности заключается в том, что при стремлении числа наблюдений к бесконечности дисперсии оценок стремятся к нулю. Это означает, что с ростом числа наблюдений их разброс становится все меньше, оценки становятся все более надежными, все плотнее концентрируются вокруг истинных значений.

Эффективность. Свойство эффективности заключается в том, что эти оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками параметров. Собственно, именно на этом и основан МНК (см. исходное соотношение (2.2)).

Практическая значимость перечисленных свойств заключается еще и в том, что с ростом объема выборки не происходит накопление регрессионных остатков.

Предпосылки мнк

Следует отметить, что вышеперечисленные свойства оценок МНК имеют место лишь при некоторых предположениях о регрессорах и случайной компоненте (регрессионном остатке) тренда. Перечислим их.

Перечень предпосылок МНК (условия Гаусса-Маркова):

1) математическое ожидание регрессионного остатка должно быть равно нулю (M(ε) = 0);

Гомоскедастичность. 2) дисперсия регрессионного остатка должна быть постоянна (это свойство называется гомоскедастичностью остатка, слово складывается из двух частей: «гомо» - однородность и «скедастичность» - разброс, вариабельность) и конечна (D(ε) = const < ∞);

Автокоррелированность. 3) значения регрессионного остатка не должны зависеть друг от друга (т.е. не должно быть автокоррелированности остатков) (Cov(ε_i, ε_j) ≈ 0, где – выборки значений случайной компоненты ε в любых двух наборах наблюдений);

4) регрессионный остаток и признаки не должны зависеть друг от друга (Cov(ε, y) ≈ 0, Cov(ε, x_j) ≈ 0, j);

5) не должно быть мультиколлинеарности (Cov(x_i, x_j) ≈ 0, i,j).

Регрессионные остатки, для которых выполняются вышеперечисленные требования, представляют собой так называемый «белый шум», т.е. независимые друг от друга значения нормально распределенной случайной величины (более подробно рассматривается при изучении стационарных временных рядов).

Последствия нарушения предпосылок МНК. Рассмотрим, что может произойти при нарушении одной или нескольких из названных предпосылок.

1) Если в регрессионном уравнении присутствует свободный член, ожидаемое значение случайной компоненты всегда равно нулю (если бы это было не так, было бы достаточно просто пересчитать свободный член). Нарушаться это требование может лишь в том случае, если по каким-либо причинам требуется, чтобы свободный член равнялся нулю или другому фиксированному значению. Тогда полученная с помощью модели оценка может оказаться смещенной.

Гетероскедастичность. 2) Гетероскедастичность, т.е. отсутствие гомоскедастичности, может привести к тому, что оценки МНК не будут обладать свойством эффективности (сама слово «гетероскедастичность» складывается из двух частей: «гетеро» - разнородность и «скедастичность» - вариабельность). Кроме того, хотя сами оценки параметров и останутся несмещенными, но стандартные ошибки этих оценок (они рассчитываются на основе дисперсии) могут оказаться смещены, что иногда приводит к неправильным результатам при проверке модели на значимость.

3) Наличие автокорреляции, как и гетероскедастичность, делает оценки неэффективными. Кроме того, оно тоже может привести к неправильному расчету стандартных ошибок модели и, как следствие, ненадежности проверки модели на значимость.

4) Если можно выявить зависимость между значениями регрессионного остатка и каким-либо из признаков, это говорит о том, что случайная компонента не является случайной по своей сути. В построенную модель необходимо внести исправления, учитывающие эту закономерность.

5) Отрицательные последствия мультиколлинеарности факторов были подробно рассмотрены ранее, а именно она затрудняет интерпретацию параметров регрессии, уменьшает точность оценок коэффициентов; приводит к росту стандартных ошибок и завышает коэффициент множественной корреляции.

Способ проверки остатков на случайный характер

Д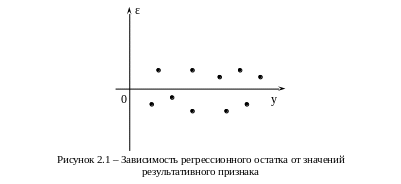 ля проверки остатков на случайный характер строят график зависимости случайной компоненты от значений результативного признака (рис. 2.1).

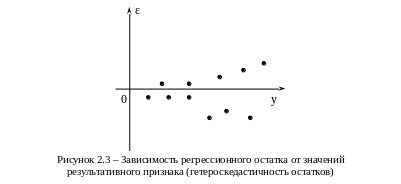
Если значения остатков расположены вблизи горизонтальной прямой (оси абсцисс), то их можно считать случайными (как на рис. 2.1). На рис. 2.2 остатки носят систематический характер. На рис. 2.3 дисперсия остатков, соответствующих большим значениям y, больше, чем дисперсия при малых y, т.е. имеет место гетероскедастичность остатков.

Кроме того, существует ряд специальных тестов, разработанных для проверики остатков на гомоскедастичность и отсутствие автокорреляции.

Тест Голдфелда-Квандта. Наиболее известным тестом для проверки на гомоскедастичность является тест Голдфелда-Квандта². Его идея заключается в том, что анализируется зависимость остатков от значений одного из признаков-факторов. Упорядочив пары наблюдений х и ε по возрастанию значений фактора х, выбирают p первых и p последних наблюдений. Если дисперсии остатков для этих двух выборок по p наблюдений различаются не слишком сильно, считают, что остатки гомоскедастичны. Таким образом, исследование свойства гомоскедастичности остатков регрессионной модели сводится к проверке гипотезы о равенстве дисперсий отклонений двух крайних групп наблюдаемых значений.

Можно доказать, что эта гипотеза принимается, если отношение суммы квадратов остатков для этих групп не превышает табличного значения критерия Фишера (чем это отношение меньше, тем ближе дисперсии друг к другу). Фактическое значение критерия Фишера F рассчитывают по формуле:

(2.12)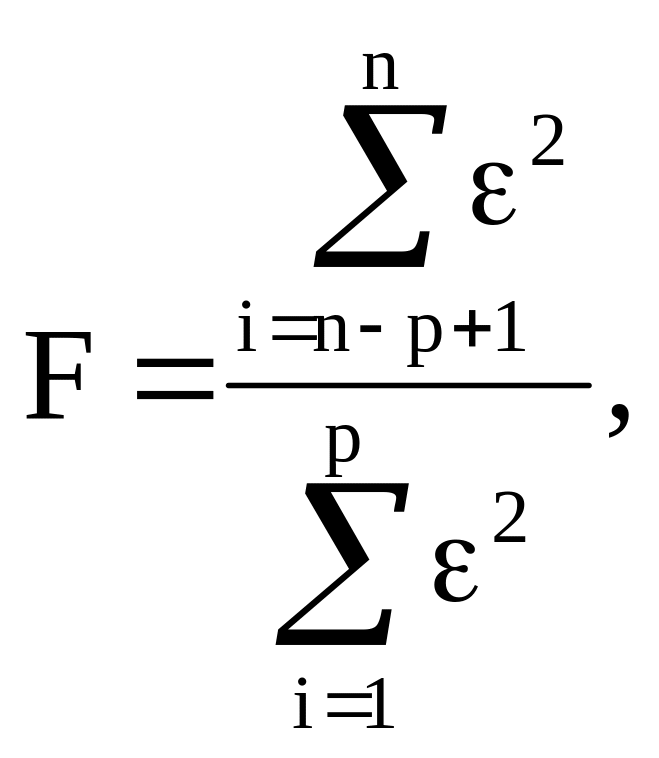

где n - число всех наблюдений,

p - число наблюдений в каждой из двух выборок,

– сумма квадратов регрессионных остатков для первых p наблюдений,

– сумма квадратов регрессионных остатков для последних p наблюдений.

Для определения табличного значения критерия Фишера необходимо задаться уровнем значимости (т.е. некоторой небольшой вероятностью того, что гипотеза о гомоскедастичности будет отвергнута случайно) и числом степеней свободы, равном (p – m), где m – число признаков-факторов.

Результаты данного теста являются наиболее достоверными, если p ≈ n/3.

Тест Дарбина-Уотсона³. Наиболее известным тестом для проверки остатков на автокорреляцию является тест Дарбина-Уотсона, в основе которого лежит сравнение расчетного критерия Дарбина-Уотсона с коэффициентом корреляции между соседними членами упорядоченного по времени ряда регрессионных остатков. Критерий Дарбина-Уотсона d рассчитывается по следующей формуле:

(2.13)

где n - число всех наблюдений,

ε_t – регрессионный остаток на момент t.

Можно доказать [Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов – М.: ЮНИТИ-ДАНА, 2003. - 311 с.], что значение этого критерия связано с коэффициентом корреляции между соседними остатками r следующим соотношением:

d

(2.14)

≈ 2*(1 – r)

Из (2.14) следует, что при отсутствии автокорреляции, т.е. r = 0, d ≈ 2. При отрицательной автокорреляции, т.е. r = -1, d ≈ 4; а при положительной r = 1, d ≈ 0.

Приближение к значениям 0, 2 и 4 определяется верхней и нижней границами d_в и d_н, которые вычислены для различных уровней значимости и приводятся в соответствующих таблицах. Отобразив значения d на числовой оси, можно схематически представить использование теста Дарбина-Уотсона в виде рисунка 2.4. При этом, если фактическое значение критерия попадает в область неопределенности, то нельзя с необходимой уверенностью ни отклонить, ни принять нулевую гипотезу, т.е. вопрос о наличии или отсутствии автокорреляции остается открытым.

Д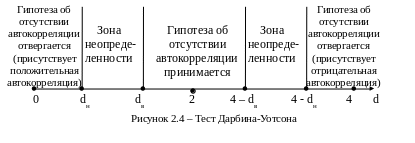 анный тест можно применять в случае, если объем выборки составляет не менее 15 наблюдений.