44

Метод наименьших квадратов (МНК) 23

Оценка параметров линейных уравнений регрессии 23

Матричная форма МНК 26

Свойства оценок, получаемых при помощи МНК 29

Предпосылки МНК 31

Обобщенный МНК 37

Исключение гетероскедастичности с помощью ОМНК 38

Исключение автокорреляции в остатках с помощью ОМНК 41

Метод наименьших квадратов (мнк) Оценка параметров линейных уравнений регрессии

Процедура построения системы нормальных уравнений и исходное соотношение, используемое в МНК. Для определения параметров функции, используемой в эконометрической модели, разработаны различные методы, наиболее простым и известным из которых является метод наименьших квадратов (МНК). Рассмотрим суть этого метода на примере парной линейной регрессии.

Применение МНК к парной линейной регрессии. Итак, необходимо определить параметры а и b для функции y = f(x) = ax + b. Пусть значения показателей y и x измерялись n раз, т.е. имеются значения показателей y₁, y₂, …, y_n и x₁, x₂, …, x_n, всего n пар значений обоих показателей. Определим сумму квадратов отклонений фактических значений признака-результата y_i от значений, подсчитанных по уравнению регрессии f(x_i):

(2.1)

Чтобы построенная модель была как можно ближе к реальности, эта сумма должна быть как можно меньше. Отметим, что полученная сумма представляет собой функцию от двух переменных а и b, и чтобы найти ее минимум, приравняем к нулю ее частные производные по а и по b:

(2.2)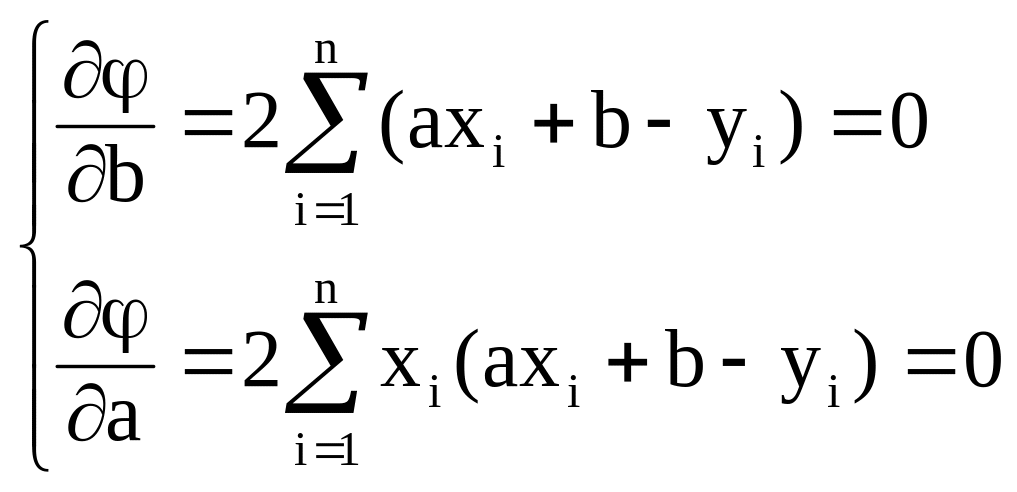

Итак, получено два линейных уравнения с двумя неизвестными – а и b (система линейна относительно параметров регрессии). Такую систему называют системой нормальных уравнений. Решив ее, можно определить искомые параметры.

Применение МНК к множественной линейной регрессии. Если необходимо определить параметры множественной линейной регрессии, т.е. параметры функции y = f(x₁, x₂, …, x_m) = a₁x₁ + a₂x₂ + … +a_mx_m + + b, имея в запасе n наблюдений для каждого признака-фактора и для признака результата, то можно аналогичным образом получить систему нормальных уравнений, состоящую из (m + 1) линейного уравнения для (m + 1) неизвестной a₁, a₂, …, a_m, b:

(2.3)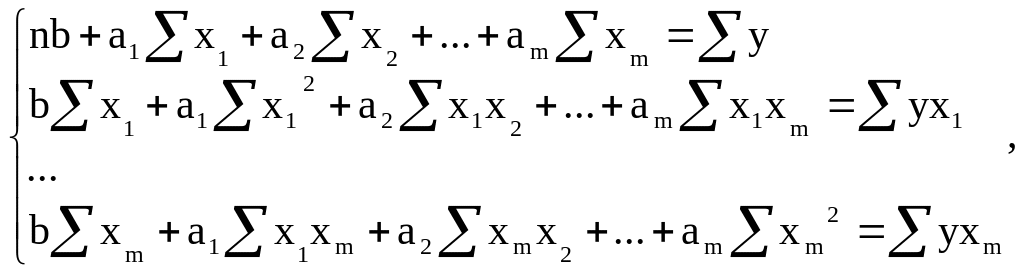

где ,

- i-ые значения наблюдаемых показателей (для каждого показателя их n).

Отметим, что систему уравнений (1.16) для нахождения стандартизованных коэффициентов регрессии также получают путем применения МНК к стандартизированному уравнению регрессии и преобразования полученных выражений.

Методы решения системы нормальных уравнений. Решение системы (2.3) может быть осуществлено различными способами:

1) в случае парной регрессии (2.2) можно выразить один параметр через другой из одного уравнения, а затем, подставив полученное выражение во второе уравнение, получить уравнение с одной переменной;

2) метод Гаусса, который заключается в том, что матрицу коэффициентов в уравнениях поэтапно преобразуют в единичную матрицу путем линейных преобразований этих уравнений (разрешающее уравнение делят на разрешающий элемент, получая на его месте единицу, а из всех остальных уравнений вычитают преобразованное разрешающее, умноженное на те коэффициенты, которые стоят в этих уравнениях в разрешающем столбце, с целью получить на их месте нули);

3) метод Крамера, который заключается в том, что рассчитывают определитель матрицы коэффициентов в уравнениях, а затем рассчитывают частные определители, поочередно заменяя один из столбцов в этой матрице столбцом свободных членов; значения переменных равны отношениям соответствующих частных определителей к определителю первой матрицы;

4) и т.д.

Рассмотрим применение первого метода более подробно:

Из второго уравнения системы (2.2) выразим b:

(2.4)

Подставим это выражение в первое уравнение:

(2.5)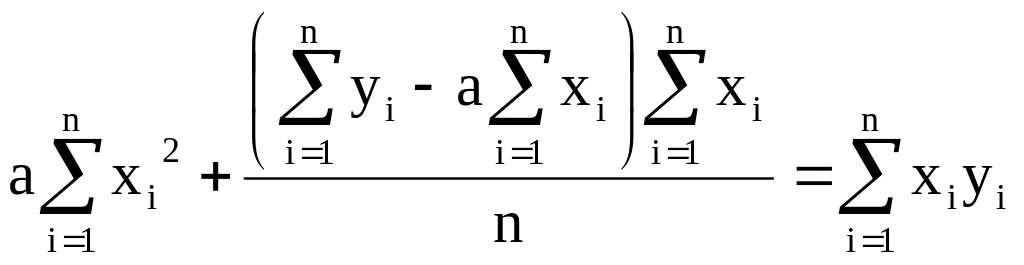

В результате алгебраических преобразований получим:

(2.6)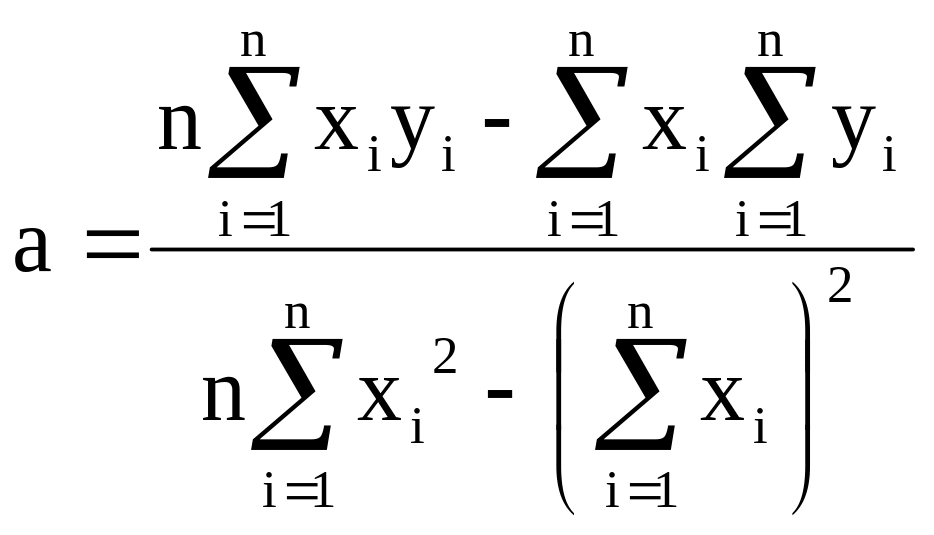

Подставив значение a в (2.4), можно найти b.

Если разделить числитель и знаменатель в формуле (2.6) на n²; а в формуле (2.4) почленно разделить числитель на n, можно получить:

(2.7)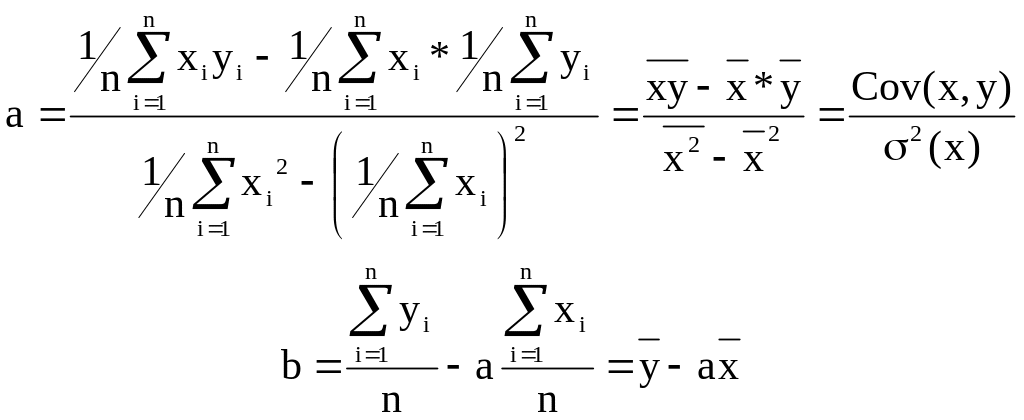

Таким образом, коэффициент парной линейной регрессии равен отношению ковариации переменных к дисперсии признака-фактора. Свободный член регрессии равен разности между средним значением результата и средним значением признака-фактора, умноженным на коэффициент регрессии.