МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПЕЧАТИ

Кафедра прикладной математики и моделирования систем

ЭКОНОМЕТРИКА

Лабораторная работа №1 “Парная регрессия”

Студент гр. Бд-3 Фамилия И.О.

Преподаватель Голинков Ю.П.

Москва

2008

Задание

Построить поле корреляции для заданной совокупности наблюдений, на основе визуального анализа удалить из выборки аномальные наблюдения (не более 5% от исходного числа), добиваясь увеличения коэффициента детерминации для линейной модели парной регрессии.

Используя встроенные функции Excel, для скорректированной выборки наблюдений построить модели парной регрессии для 6 заданных функций регрессии: линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической. Для каждой из построенных моделей определить коэффициент детерминации, среднюю ошибку аппроксимации, коэффициент эластичности. Прокомментировать качество построенных моделей.

Привести расчетные формулы и выполнить вычисления параметров уравнения парной линейной регрессии, показателей статистической значимости уравнения регрессии в целом, коэффициентов регрессии и корреляции, точечного и интервального прогноза. Используя надстройку Excel “Анализ данных” и матричные вычисления, продублировать вычисления параметров модели парной линейной регрессии и всех показателей, характеризующих ее качество.

С помощью пакета STATISTICA провести расчеты для линейной, гиперболической и обратной функций регрессии. Построить график с доверительными интервалами прогноза для линейной регрессии.

Проанализировать возможность улучшения качества модели регрессии за счет применения нелинейных функций регрессии и удаления некоторых наблюдений (не более 10%).

Исходные данные

Поле корреляции по исходным данным

Выявление и удаление аномальных наблюдений

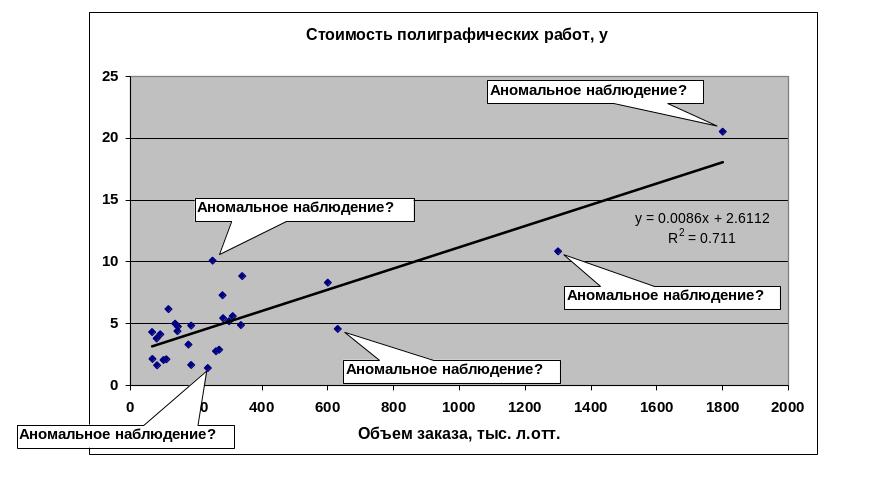
Значения коэффициента детерминации для исходной выборки и после поочередного удаления предполагаемых на основе визуального анализа аномальных наблюдений:

Исходная выборка		0.711
235.2	1.42	0.7266
250	10.1	0.7704
630	4.58	0.7415
1300	10.86	0.7181
1800	20.54	0.3879

По результатам проведенного анализа из выборки удалено наблюдение (10,1; 250).

Скорректированная выборка (27 наблюдений)

Описательная статистика

Модели парной регрессии

Линейная

Степенная

Экспоненциальная

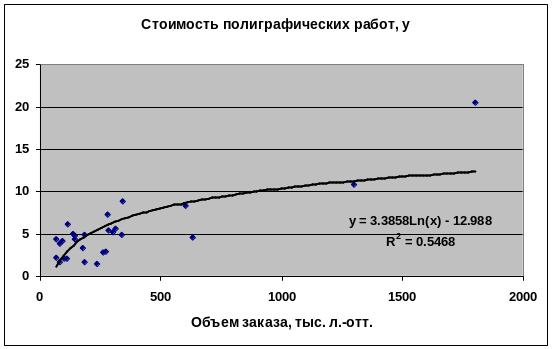
Логарифмическая

Обратная

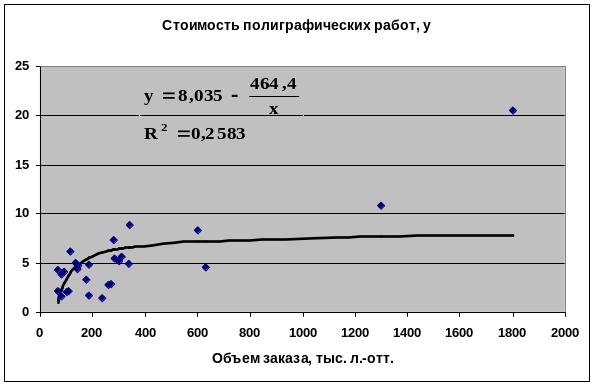
Гиперболическая

Расчетные формулы

Коэффициент детерминации

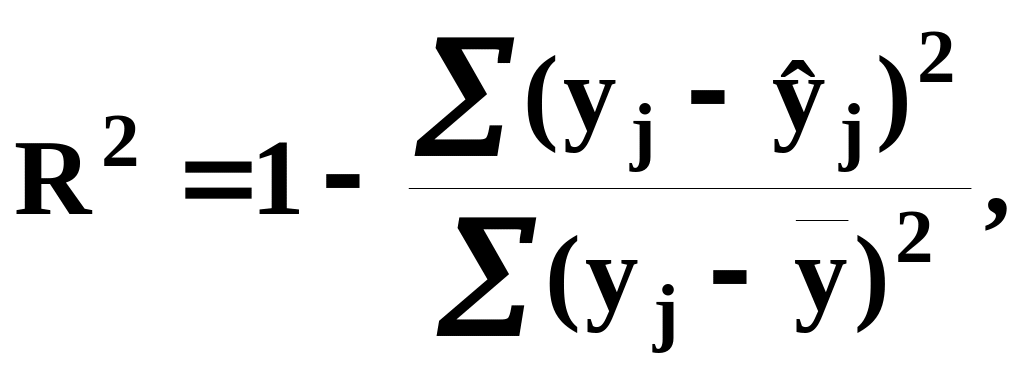
где - наблюдавшееся значение результативного показателя;

- расчетное значение по уравнению регрессии;

- среднее значение результативного показателя.

Коэффициент детерминации рассчитывался для обратной функции регрессии:

и для гиперболической функции регрессии:

для остальных функций получен с помощью команды Excel Диаграмма_Добавить линию тренда.

Средняя ошибка аппроксимации

Для расчета средней ошибки аппроксимации использовались формулы:

,

.

Для каждой модели выбиралось минимальное из трех рассчитанных значений.

Коэффициент эластичности

Для линейной функции:

Для степенной функции:

Для экспоненциальной функции:

Для полулогарифмической функции:

Для обратной функции:

Для гиперболической функции:

Сравнительная характеристика моделей

Вид модели	Коэффициент детерминации	Средняя ошибка аппроксимации	Коэффициент эластичности
Линейная	0.7704	29.79%	0.5383
Степенная	0.4429	27.60%	0.4892
Экспоненциальная	0.4803	29.98%	0.3513
Логарифмическая	0.5468	36.60%	0.5180
Обратная	0.2364	35.91%	0.1804
Гиперболическая	0.2583	42.92%	0.2209

Из рассмотренных моделей наибольшее значение коэффициента детерминации, близкое к требуемой величине 0.8, имеет линейная модель. Однако, высокая величина средней ошибки аппроксимации (около 30%) ограничивает возможность ее практического применения. Ни одна из других моделей не соответствует предъявляемым требованиям по величине коэффициента детерминации и средней ошибки аппроксимации.