
- •Проводные и кабельные линии связи.
- •Первичные параметры электрических линий.
- •Кабели на основе витых пар
- •Коаксиальные кабели
- •Оптоволоконные кабели
- •Бескабельные каналы связи
- •Длинные линии
- •Тема 18. Передача сигналов по кабелям Содержание
- •Введение
- •18.1. Основное уравнение кабельной линии [7,23]
- •18.2. Волновое сопротивление кабельной линии [7,23]
- •18.3. Режимы передачи сигналов кабельной линией [7,23]
- •Литература
18.2. Волновое сопротивление кабельной линии [7,23]
Волновое сопротивление – это сопротивление линии электромагнитной волне при отсутствии отражений от концов линии. Оно зависит от первичных электрических параметров кабеля и частоты сигнала. Если электромагнитную волну представить в виде раздельных волн напряжения и тока, то соотношение между ними и представляет собой волновое сопротивление цепи:
= / .
Рис. 18.2.1.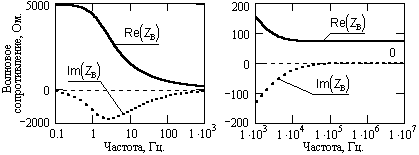
Как
следует из рисунка, зависимость волнового
сопротивления от частоты наиболее
существенна в области низких частот
(менее 10 кГц) и имеет емкостной характер.
В области частот более 10-20 кГц имеет
место L
> R, C
>> G и значение волнового сопротивления
стремится к постоянной величине
![]() .
Эту величину называют номинальным
(характеристическим) волновым
сопротивлением кабеля. В дальнейшем
индексом Zв
=
Rв
будем обозначать постоянное
характеристическое сопротивление
кабеля (на частотах более 50-100 кГц). Для
частотной функции волнового сопротивления
будем применять обозначение с аргументом
по частоте Zв()
или индекс
.
.
Эту величину называют номинальным
(характеристическим) волновым
сопротивлением кабеля. В дальнейшем
индексом Zв
=
Rв
будем обозначать постоянное
характеристическое сопротивление
кабеля (на частотах более 50-100 кГц). Для
частотной функции волнового сопротивления
будем применять обозначение с аргументом
по частоте Zв()
или индекс
.
Рис. 18.2.2. Модуль
и фаза волнового сопротивления.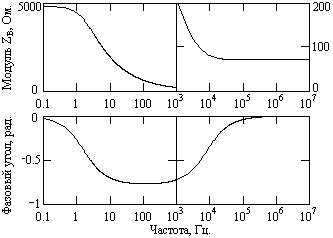
Zв() = zв() exp(jв()),
где: zв() – частотная функция модуля волнового сопротивления (абсолютная величина отношения амплитудных значений напряжения и тока по аргументу – частоте ) в любой точке линии, - частотная функция угловых значений, равных разности фаз волн напряжения и тока. Частотная зависимость значений модуля и фазового угла волнового сопротивления приведена на рис. 18.2.2. Как следует из графиков, волна тока в области низких частот опережает волну напряжения в максимуме на 45о.
Рис. 18.2.3. Частотные функции
и 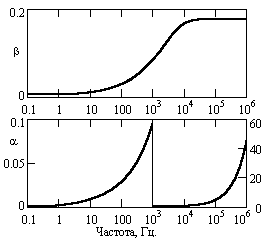
=
0.5(R![]() + G
).
+ G
).
Рис. 18.2.4. Частотные функции
и 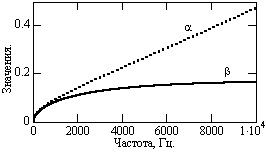
![]() ).
Это обеспечивает формирование фронтальной
волны распространения сигнала по кабелю
с постоянной скоростью для всех частотных
составляющих сигнала, за исключением
низких частот, и сохранение формы
сигналов на нагрузке. Отсюда следует,
что кабель является оптимальной линией
передачи высокочастотных и радиоимпульсных
сигналов, энергия частотного спектра
которых минимальна в области низких
частот.
).
Это обеспечивает формирование фронтальной
волны распространения сигнала по кабелю
с постоянной скоростью для всех частотных
составляющих сигнала, за исключением
низких частот, и сохранение формы
сигналов на нагрузке. Отсюда следует,
что кабель является оптимальной линией
передачи высокочастотных и радиоимпульсных
сигналов, энергия частотного спектра
которых минимальна в области низких
частот.
При совместном рассмотрении рисунков 18.2.1-18.2.4 нетрудно сделать вывод, что, начиная с частот порядка 5-10 кГц, кабельные линии связи имеют практически постоянные параметры. Именно в этой частотной области обеспечиваются минимальные искажения формы частотного спектра сигналов, а соответственно и формы самих сигналов при их передаче по линии связи.
Коэффициент передачи сигнала по напряжению по кабельной линии в общем виде может быть определен из выражения (18.1.1):
![]() =
/
=
ch
– (
/
)sh
,
(18.2.1)
=
/
=
ch
– (
/
)sh
,
(18.2.1)
=
ch
– (
/![]() )sh
,
(18.2.1')
)sh
,
(18.2.1')
где – длина кабеля, Zвх – входное сопротивление кабеля, которое также является комплексной величиной и зависит от частоты:
= (Zн ch + sh ) / ( ch + Zн sh ). (18.2.2)
