
- •Введение
- •1 Расчёт магнитоэлектрической системы.
- •Исходные данные.
- •1.2 Расчёт длины и диаметра магнита.
- •1.3 Определение индукции в зазоре.
- •2 Расчёт электромагнитной системы.
- •2.1 Исходные данные.
- •2.2. Определение количества витков катушки.
- •2.3. Определение магнитного сопротивления при
- •2.4 Расчет чувствительности преобразователя.
- •2.5 Расчет измерительного усилия преобразователя.
- •Список литературы
2.1 Исходные данные.
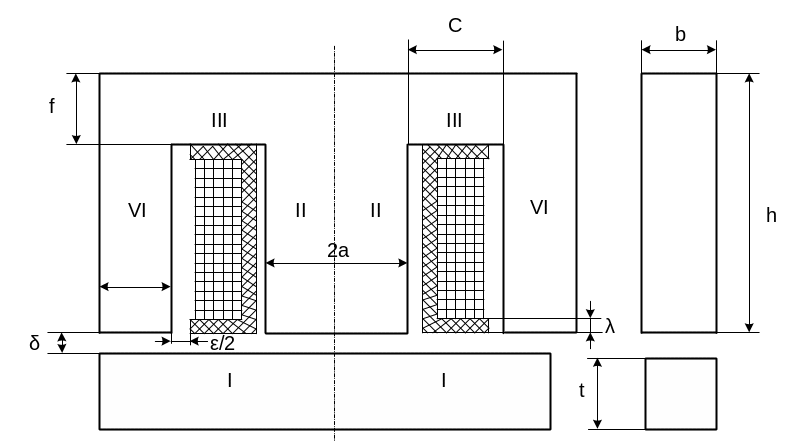
Рисунок 2.1. Схема Ш – образной магнитоэлектрической системы
Магнитная цепь обычно выполняется симметричной относительно среднего сердечника, на котором расположена катушка. Поэтому достаточно рассчитать одну ее половину, уменьшив сечение среднего сердечника вдвое и сохранив ту же величину намагничивающей силы катушки.
Рассчитаем электромагнитной системы с заданными габаритными размерами (см. рис.2.1):
![]() ,
,
![]() ,
,
![]() ,
,![]() - зазор между каркасом и сердечником,
предел измерения
- зазор между каркасом и сердечником,
предел измерения
![]() ,
,![]() - толщина стенок каркаса катушки,
измерительное усилие не более
- толщина стенок каркаса катушки,
измерительное усилие не более
![]() ,
чувствительность
,
чувствительность![]() ,
,
![]() - частота питающего напряжения.
- частота питающего напряжения.
2.2. Определение количества витков катушки.
Определяем количество витков катушки, предварительно задавшись диаметром и маркой провода.
ПЭВ 1, с
![]() 0,60мм
0,60мм
![]()
Начальный зазор
определяется выражением:
![]()
![]()
![]()
Следовательно,
выбираем
![]()
![]()
![]()
Зададимся величиной
индукции в среднем сердечнике:
![]()
При расчете магнитной цепи удобно использовать схемы замещения. Схема замещения (рис.2.2.) составляется сообразно конфигурациям магнитопровода. Все участки магнитных сопротивлений цепи на схеме обозначены сосредоточенными магнитными сопротивлениями, а магнитодвижущая сила F катушки показана как источник питания.

Рисунок 2.2. Схема замещения магнитной цепи для Ш-образного сердечника с катушкой и якорем
![]() магнитное
сопротивление i-го
стального участка;
магнитное
сопротивление i-го
стального участка;
![]() сопротивление
i-го
воздушного зазора.
сопротивление
i-го
воздушного зазора.
Все участки сопротивлений магнитной цепи обозначены сосредоточенными магнитными сопротивлениями.
![]() МДС
катушки – источник потока
МДС
катушки – источник потока
![]() .
.
Т.к. рассматриваемая
цепь симметрична, то условно принимаем,
что сопротивление среднего сердечника
состоит из 2-х равных параллельно
включенных магнитных сопротивлений
![]() и 2-х равных сопротивлений воздушных
зазоров
и 2-х равных сопротивлений воздушных
зазоров
![]() .
.
Для любой половины
магнитопровода полная магнитное
сопротивление цепи будет
![]() равна
сумме сопротивлений стальных участков
в магнитной цепи
равна
сумме сопротивлений стальных участков
в магнитной цепи
![]() и сумме сопротивлений 2-х воздушных
зазоров
и сумме сопротивлений 2-х воздушных
зазоров
![]() и
и
![]() :
:
![]()
Поскольку мы
пренебрегаем величинами сопротивлений
стальных участков
![]() ,
тогда суммарное сопротивление
,
тогда суммарное сопротивление
![]()
Общий магнитный
поток, создаваемый катушкой преобразователя,
равен:
![]() ,
,
где
![]() магнитный
поток левой и правой части магнитопровода.
магнитный
поток левой и правой части магнитопровода.
2.3. Определение магнитного сопротивления при
максимальном и минимальном воздушных зазорах.
Определяем магнитное
сопротивление воздушных зазоров при
минимальном и максимальном значении
![]() .
При расчете обычно пользуются магнитной
проводимостью воздушных зазоров, т.е.
величиной обратной
.
При расчете обычно пользуются магнитной
проводимостью воздушных зазоров, т.е.
величиной обратной
![]() :
:
![]()
Магнитное поле в зазоре не является плоскопараллельным. Магнитный поток «выпучивается» из-под полюсов, поэтому для расчета проводимости воздушного зазора применяют метод разбивки поля на простые геометрические фигуры, проводимость которых затем определяется по известным формулам. В нашем случае поле разбивается на 8 простых фигур.
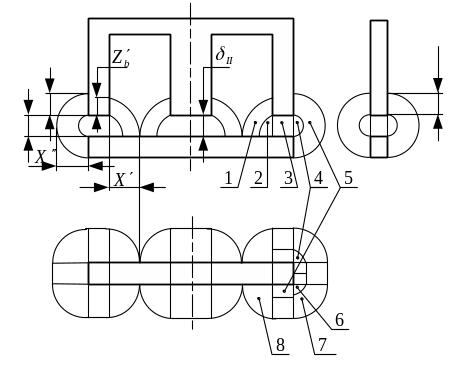
Рисунок 2.3. Картина магнитного поля в воздушном зазоре
Координаты
полей выпучивания
![]() определяются по графику (рисунок 2.4.).
определяются по графику (рисунок 2.4.).
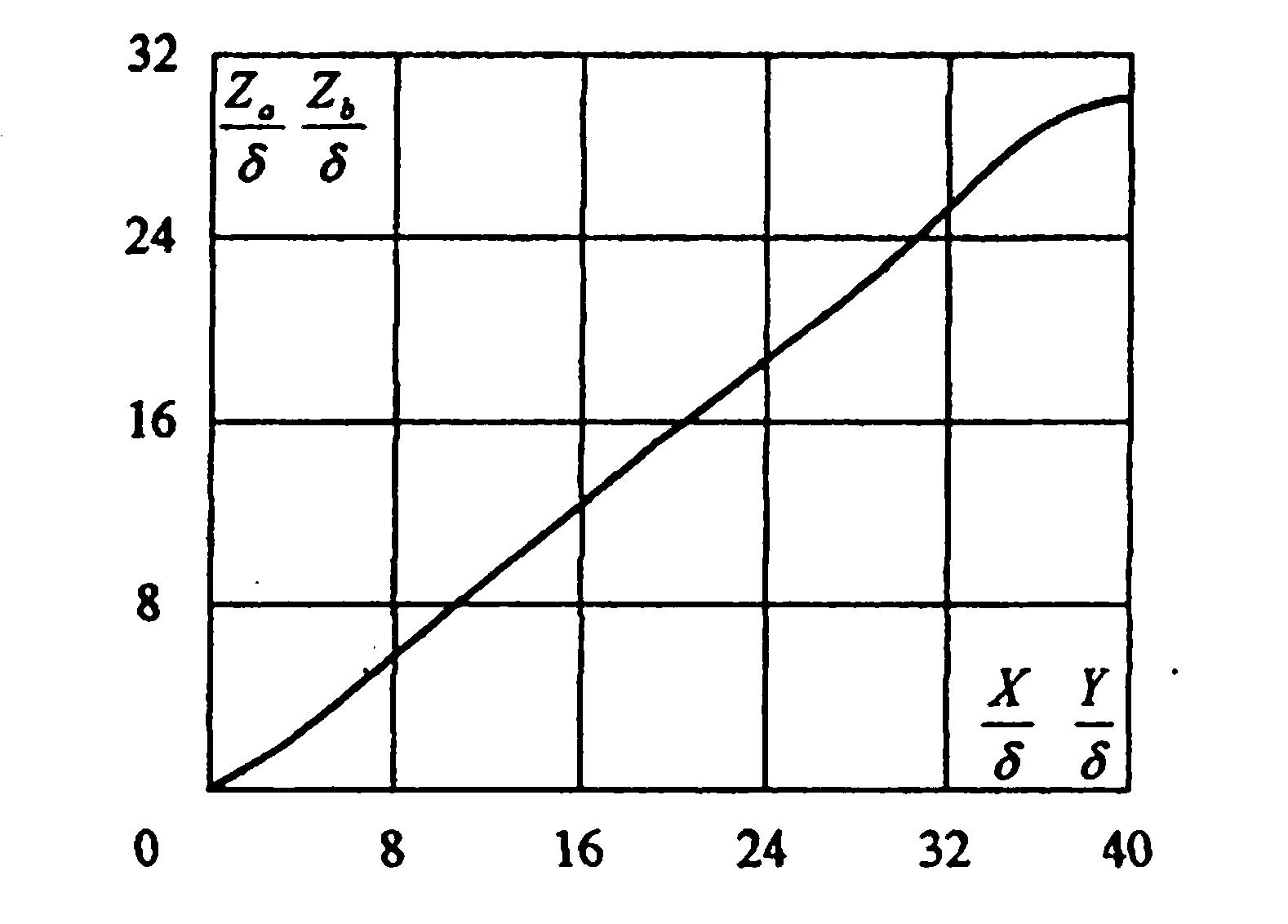
Рисунок 2.4. Зависимость между координатами поля выпучивания
Координата
![]() обычно принимается равной
обычно принимается равной
![]() ,
,
![]() расстояние между сердечниками.
расстояние между сердечниками.
![]()
Расчет удобно начинать с максимальной длины зазора при которой ток, проходящий через катушку преобразователя имеет наибольшее значение (если катушка питается напряжением). Если при этих условиях определить параметры катушки, то плотность тока в процессе работы не превысит расчетной величины.
Из графика,
по известному отношению
![]() определяем:
определяем:
![]() ,
откуда
,
откуда
![]() .
.
С достаточной
для практики точностью принимают
![]() .
.
Аналогично,
по известному отношению:
![]() .
Определяем по графику
.
Определяем по графику
![]() .
.
Далее определяем проводимости участков, показанных на рисунке 2.3:
проводимость одной четверти полого цилиндра
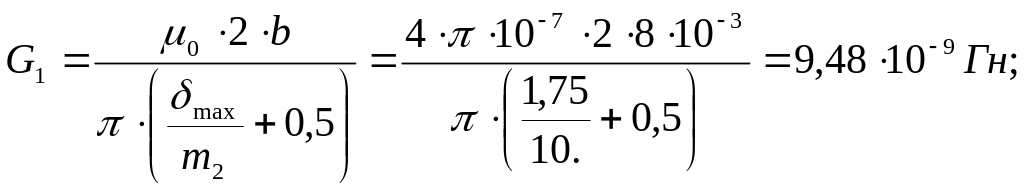
где
![]() ;
;
проводимость 1/4 цилиндра
![]() ;
;
проводимость куба (зазор под полюсами)
![]() ;
;
проводимость 1/2 цилиндра
![]() ;
;
проводимость ½ полого цилиндра
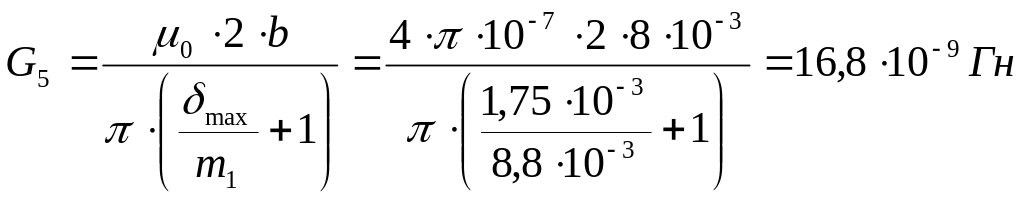 ,
,
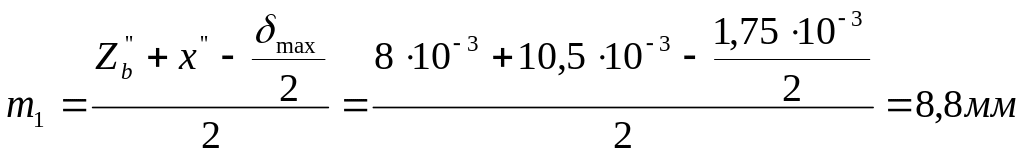 - средняя толщина
стенки цилиндра;
- средняя толщина
стенки цилиндра;
проводимость шарового квадранта
![]() ;
;
проводимость квадранта полого шара
![]() ;
;
проводимость квадрантов сложной формы , заключенных между фигурами 1,2,6,7
![]() .
.
Магнитная проводимость воздушных зазоров определяется как сумма их составляющих:
Для зазора
![]()
![]()
Магнитное
сопротивление зазора
![]()
Для зазора
![]()
![]() Магнитное
сопротивление зазора
Магнитное
сопротивление зазора
![]()
![]()
Тогда суммарное
магнитное сопротивление магнитной цепи
преобразователя будет:
![]()
Магнитное
сопротивление половины индуктивного
преобразователя усилия
![]() .
.
Зная магнитное
сопротивление всей цепи, можно определить
полное электрическое сопротивление
![]() катушки преобразователя:
катушки преобразователя:
![]() ;
;
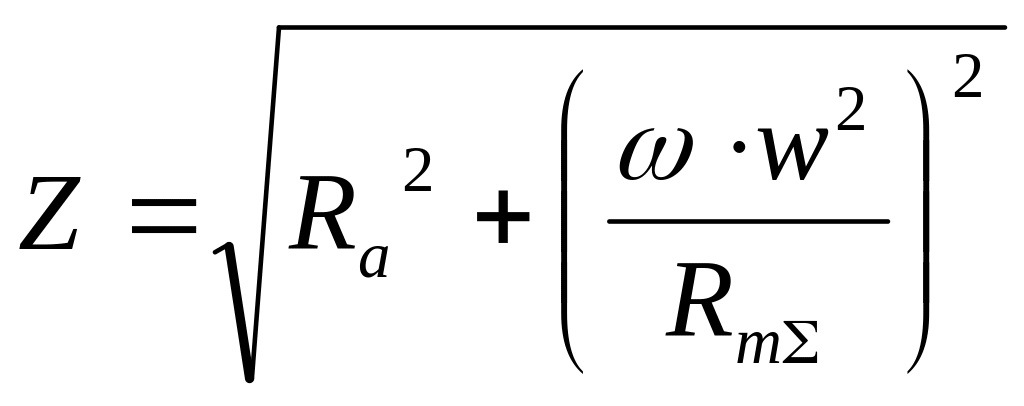 ,
где
,
где
![]() активное сопротивление катушки
преобразователя;
активное сопротивление катушки
преобразователя;
![]() - круговая частота;
- частота.
- круговая частота;
- частота.
![]() ,
где
,
где
![]() - удельное сопротивление меди;
- удельное сопротивление меди;
![]() - средняя длина
витка;
- средняя длина
витка;
![]() -
поперечное сечение голого провода.
-
поперечное сечение голого провода.
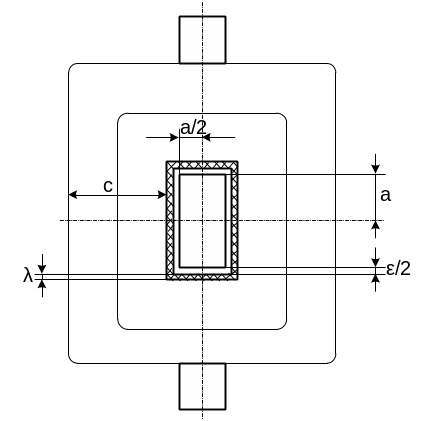
Рисунок 2.5. Схема расположения катушки на сердечнике электромагнитной системы
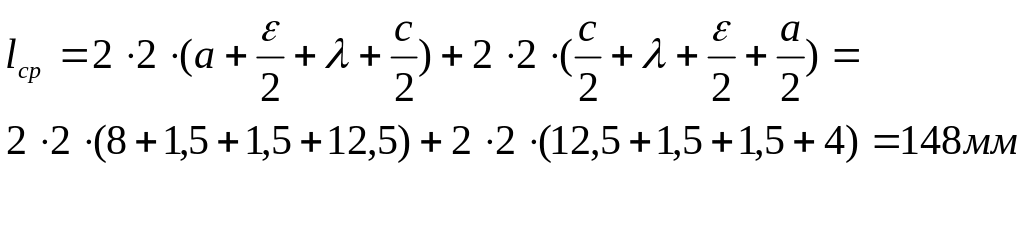
![]()
![]()
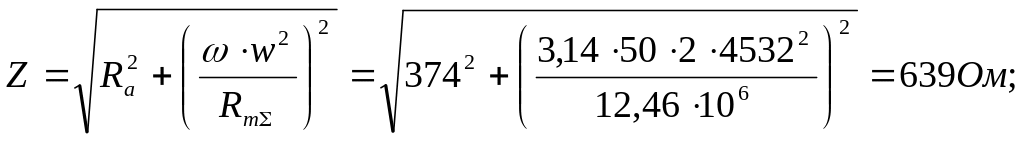
Эффективное
значение тока, протекающего через
катушку преобразователя, для создания
выбранной магнитной индукции
![]() ,
составит:
,
составит:
![]()
Плотность тока в
обмотке не должна превышать
![]()
![]() плотность тока не
превышает предельное значение
плотность тока не
превышает предельное значение
Напряжение питания
катушки
![]() .
.
Для приближенного определения чувствительности преобразователя и измерительного усилия необходимо определить сопротивление магнитной цепи и электрического сопротивление катушки при минимальном зазоре:
![]()
Из графика, по
известному отношению
![]() определяем:
определяем:
![]() ,
откуда
,
откуда
![]() .
.
С достаточной для практики точностью принимают .
Аналогично, по
известному отношению
![]() .
Определяем по графику
.
Определяем по графику
![]() .
.
Далее определяем проводимости участков, показанных на рисунке 2.3:
1)проводимость одной четверти полого цилиндра
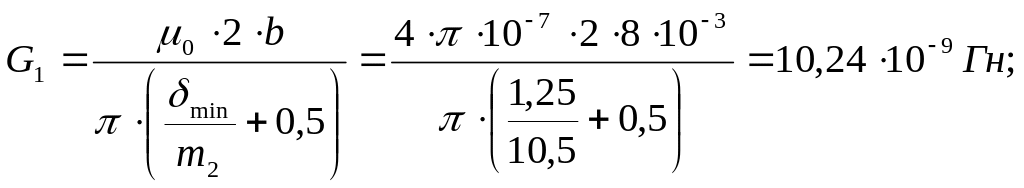
где
![]() ;
;
проводимость 1/4 цилиндра
![]() ;
;
проводимость куба (зазор под полюсами)
![]() ;
;
проводимость 1/2 цилиндра
![]() ;
;
проводимость ½ полого цилиндра
 ,
,
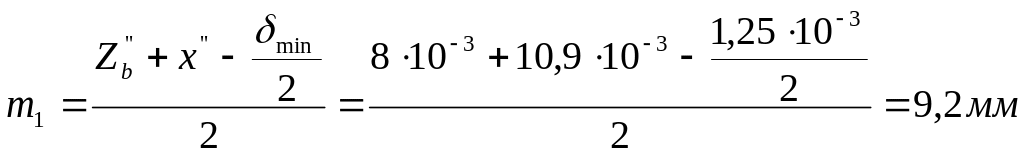 - средняя толщина
стенки цилиндра;
- средняя толщина
стенки цилиндра;
проводимость шарового квадранта
![]() ;
;
проводимость квадранта полого шара
![]() ;
;
проводимость квадрантов сложной формы , заключенных между фигурами 1,2,6,7
![]() .
.
Магнитная проводимость воздушных зазоров определяется как сумма их составляющих:
Для зазора
![]()
Магнитное
сопротивление зазора
![]()
Для зазора
![]() Магнитное
сопротивление зазора
Магнитное
сопротивление зазора
![]()
Тогда суммарное
магнитное сопротивление магнитной цепи
преобразователя будет:
![]() .
.
Магнитное
сопротивление половины индуктивного
преобразователя усилия
![]() .
.
Зная магнитное сопротивление всей цепи, можно определить полное электрическое сопротивление катушки преобразователя:
;
, где активное сопротивление катушки преобразователя; - круговая частота; - частота.
, где - удельное сопротивление меди;
- средняя длина витка; - поперечное сечение голого провода.

