3.8. Мода и медиана. Моменты случайных величин. Асимметрия и эксцесс

Кроме математического ожидания и дисперсии применяется еще ряд числовых характеристик, отражающих те или иные особенности распределения случайной величины.

Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение (для которого вероятность р_i или плотность вероятности f(х) достигает максимума).

Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках, распределение называется полимодальным.

Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, для которого

F(Me(X))=Р(Х < Ме(Х)) = Р(Х > Ме(Х)) = 0,5,

то есть вероятность того, что случайная величина Х примет значение, меньшее медианы Ме(Х) или большее ее, одна и та же и равна 0,5.

Геометрически вертикальная прямая х = Ме(Х), проходящая через точку с абсциссой, равной Ме(Х), делит площадь фигуры под кривой распределения на две равные части.

Пример 3.8.1. Найти моду, медиану и математическое ожидание случайной величины Х с плотностью вероятности f(х) = 3х² при х[0;1].

Решение.

Очевидно, что плотность вероятности f(х) максимальна при х = Мо(X)=1.

Медиану Ме(Х)=b найдем из условия:

или

откуда .

Математическое ожидание:

.

Среди числовых характеристик случайной величины особое значение имеют моменты — начальные и центральные.

Начальным моментом k-го порядка случайной величины Х называется математическое ожидание k -ой степени этой величины:

.

Центральным моментом k-го порядка случайной величины Х называется математическое ожидание k -ой степени отклонения случайной величины от ее математического ожидания:

или

, где а=М(Х).

Формулы для вычисления моментов для дискретных и непрерывных случайных величин приведены в таблице.

Момент	Случайная величина
	Дискретная	Непрерывная
Начальный
Центральный

При k = 1 первый начальный момент случайной величины Х есть ее математическое ожидание, то есть , а при k = 2 второй центральный момент — дисперсия, то есть .

Центральные моменты могут быть выражены через начальные моменты по формуле:

.

В частности,

;

;

;

.

Таким образом, математическое ожидание М(Х), или первый начальный момент ₁, характеризует среднее значение или положение распределения случайной величины X, а дисперсия D(Х), или второй центральный момент ₂ — степень рассеяния распределения X относительно М(Х).

Для более подробного описания распределения служат моменты высших порядков.

Третий центральный момент ₃ служит для характеристики асимметрии (скошенности) распределения. Он имеет размерность куба случайной величины. Чтобы получить безразмерную величину, ее делят на σ³, где σ — среднее квадратическое отклонение случайной величины X. Полученная величина А называется коэффициентом асимметрии случайной величины:

.

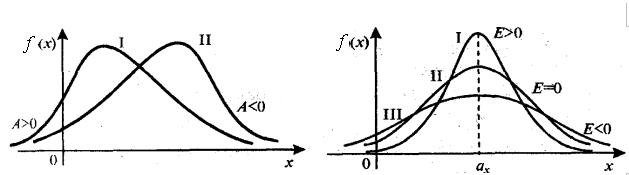
Рис. 3.8.1. Рис. 3.8.2.

Если распределение симметрично относительно математического ожидания, то коэффициент асимметрии А = 0. Если А < 0, то это говорит о большом влиянии на μ₃ отрицательных отклонений, то есть распределение имеет отрицательную (левостороннюю) асимметрию. В этом случае кривая более полога слева от математического ожидания а_х. Аналогично для случая А > 0 (рис. 3.8.1, 3.8.2).

Четвертый центральный момент ₄ служит для характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом случайной величины называется число

.