Глава 3 Случайные величины

3.1. Понятие случайной величины

Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее не известно).

Случайной величиной Х называется числовая функция, заданная на пространстве элементарных событий Ω: Х = f(ω), где ω – элементарный исход (или элементарное событие, принадлежащее пространству Ω).

Случайная величина называется дискретной, если множество ее значений конечное, или бесконечное, но счетное.

Под непрерывной случайной величиной будем понимать величину, бесконечное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, графически и аналитически (в виде формулы). Простейшей формой задания закона распределения дискретной случайной величины Х является таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие им вероятности, то есть

х1	x2	…	xi	...	хп
р1	р2	…	рi	…	рп

Такая таблица называется рядом распределения дискретной случайной величины. События Х= х₁, …, Х= х_п образуют полную группу. Следовательно, сумма их вероятностей равна 1, то есть .

Для наглядности закон распределения дискретной случайной величины изображают графически, для чего в прямоугольной системе координат строят точки (x_i; p_i) и соединяют последовательно отрезками прямых. Получающаяся при этом ломаная линия называется многоугольником распределения случайной величины х (рис. 3.1.1).

Рис. 3.1.1.

Пример.3.1.1. В лотерее разыгрываются: один автомобиль стоимостью 5000 ден. ед., четыре телевизора стоимостью 250 ден. ед., пять видеомагнитофонов стоимостью 200 ден. ед. Всего продается 1000 билетов по 50 ден. ед. Составить закон распределения случайной величины Х — суммы чистого выигрыша, полученного участником лотереи, купившим один билет.

Решение. Возможные значения случайной величины Х — суммы чистого выигрыша на один билет равны:

х₁ = 0 – 50 = – 50 ден. ед. (если билет не выиграл),

х₂ =200 – 50 = 150 ден. ед. (если на билет выпал выигрыш видеомагнитофона),

х₃ =250 – 50 = 200 ден. ед. (если на билет выпал выигрыш телевизора),

х₄ =5000 – 50 = 4950 ден. ед. (если на билет выпал выигрыш автомобиля).

Учитывая, что из 1000 билетов число невыигравших составляет 990, а указанных выигрышей соответственно 5, 4 и 1, и, используя классическое определение вероятности, получим:

р₁ = Р(Х=–50) = 990/1000=0,990;

р₂ = Р(Х=150) =5/1000=0,005;

р₃ = Р(Х=200) =4/1000=0,004;

р₄ = Р(Х=4950)= 1/1000=0,001,

тогда закон распределения случайной величины Х — суммы чистого выигрыша на один билет имеет вид:

xi	-50	150	200	4950
рi	0,990	0,005	0,004	0,001

Пример.3.1.2. В урне 7 шаров, из которых 4 белых, а остальные черные. Из неё наудачу извлекаются 3 шара. Составить закон распределения случайной величины Х – числа белых шаров, среди извлеченных из урны трёх. Найти вероятность того, что Х примет значение не менее 2.

Решение. Случайная величина Х может принимать следующие значения:

– ни одного белого шара среди извлечённых трёх;

– только один белый шар среди извлечённых трёх;

– только два белых шара среди извлечённых трёх;

– все три извлечённых шара белые;

Тогда соответствующие им вероятности р₁, р₂, р₃, р₄ подсчитываем классическим способом:

; ;

;

Закон распределения случайной величины Х имеет вид:

xi	0	1	2	3
pi

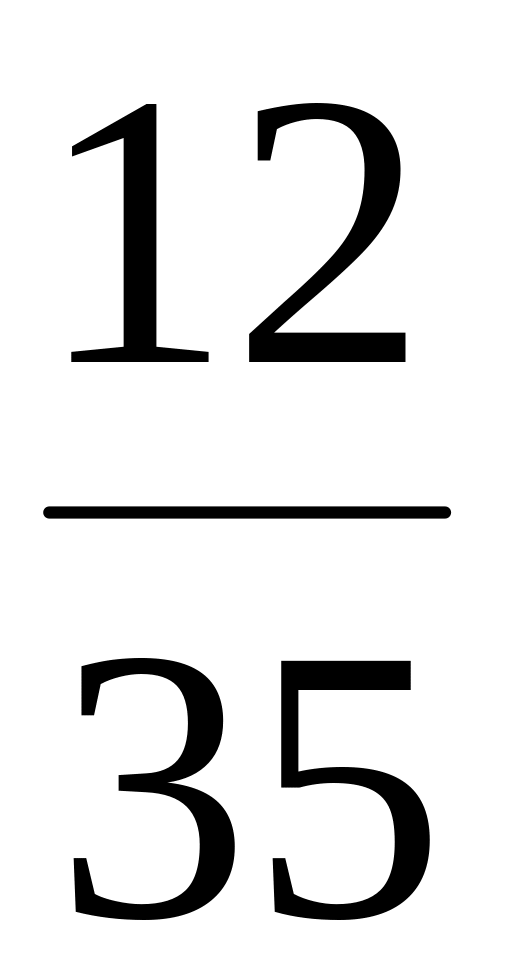
Найдём вероятность того, что случайная величина Х примет значение не менее 2 (Х  2), то есть случайная величина Х примет значение 2 с вероятностью 18/35 или значение 3 с вероятностью 4/35. Тогда вероятность события Х  2 равна:

Р (Х  2) = + = .