3. Синтез модального управления и наблюдающего устройства полного порядка для объекта с векторным входом и векторным выходом

 

Неустойчивую систему управления можно сделать асимптотически устойчивой при охвате ее матрицей обратной связи по всем переменных состояния. Это означает, что если система имеет модель вида

 (6.24)

то, приняв управление U в виде

, (6.25)

где  – матрица регулятора, замкнутая на это управление система будет иметь вид

 (6.26)

Динамика системы (6.26) будет определяться собственными числами матрицы  . Описание системы с модальным управлением и наблюдателем имеет вид

 (6.27)

где  – матрица усиления наблюдателя размера nm, m – размерность вектора выхода, n – размерность вектора состояния исходной системы.

В соответствии с теоремой разделимости [10, 11] расчет матрицы усиления регулятора   и матрицы усиления наблюдателя   можно производить независимо друг от друга. На рис. 6.1 показана схема моделирования системы управления с модальным регулятором и наблюдателем.

Рис. 6.1. Схема системы управления с регулятором и наблюдателем

На рис. 6.1 пунктирная стрелка обозначает возможное подключение воздействия к синтезированной системе управления.

Синтез наблюдающих устройств пониженного порядка для линейных стационарных систем управления

 

Цель работы: освоить методы синтеза асимптотических наблюдающих устройств (наблюдателей) пониженного порядка для линейных стационарных непрерывных систем управления при отсутствии случайных помех; проанализировать динамические свойства систем управления с наблюдателем.

 

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

 

Задачу синтеза наблюдающего устройства пониженного порядка будем рассматривать для линейной системы с векторным входом и векторным выходом

 (7.1)

 (7.2)

где Х(t) – n-мерный вектор состояния, U(t) – r-мерный вектор управления, Y(t) – m-мерный выход, А, В, С – матрицы действительных чисел размеров nn, nr, mn соответственно, и полный вектор состояния не доступен для измерения (наблюдения). При этом m ≤ n, r ≤ n.

Оценку вектора состояния можно получить с помощью динамической системы, которая имеет размерность (n – m)-го порядка.

Уравнение выхода исходной системы (7.2) определяет m линейных комбинаций относительно вектора состояния X(t). Тогда можно поставить задачу определения (n – m) подобных комбинаций. Эти (n – m) линейных комбинаций можно получить с помощью наблюдателя (n – m)-го порядка. Наблюдатели пониженного порядка, использующие информацию о входе и выходе исходной системы, называются наблюдателями Люенбергера, если динамика наблюдателя определяется из условий его устойчивости.

Для восстановления вектора состояния исходной системы (7.1) уравнение наблюдателя пониженного порядка имеет вид [11, 20]

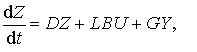 (7.3)

где Z – (n – m)-й вектор, D – устойчивая матрица размера (n – m)(n – m), G – произвольная матрица размера (n – m)m,L – матрица преобразования размера (n – m)n, Y = CX.

Если считать Z(t) = LX(t) для всех t  0, то решение уравнения (7.3) имеет вид

, (7.4)

где Z(0) – (n – m)-мерный вектор начальных условий, Х(0) – n-мерный вектор начальных условий. Если матрица D имеет отрицательные собственные значения, то при t   получим, что Z(t)  LX(t). При этом матрица L должна быть решением обобщенного матричного уравнения Ляпунова (Сильвестра):

. (7.5)

После определения вектора Z(t) будем иметь (n – m) линейных комбинаций, связывающих между собой выход наблюдающего устройства Z(t) и вектор состояния исходной системы: Z(t) = LX(t). Поскольку в соответствии с (7.4) вектор Z(t) стремится к X(t) асимптотически, то можно говорить, что Z(t) определяет собой оценку соотношения LX(t).

Выпишем уравнения линейных комбинаций:

 (7.6)

Объединим уравнения (7.6) в одно матричное уравнение:

 (7.7)

В (7.7) матрицу, состоящую из С и L, обозначим через Р:

 (7.8)

Матрица Р имеет размерность nn, и ее ранг равен n, т. е. Р – невырожденная матрица. Из (7.7) с учетомневырожденности матрицы Р можно получить оценку вектора X(t):

, (7.9)

где обозначение   принято по той причине, что вектор Z(t) стремится к LX(t) только асимптотически.

Соотношение (7.9) можно представить в виде

, (7.10)

где   

Е – единичная матрица порядка n.

Выпишем векторные уравнения системы и наблюдателя для моделирования:

 (7.11)

 (7.12)

 (7.13)

 (7.14)

 (7.15)

Таким образом, синтез наблюдателя пониженного порядка для линейной стационарной системы управления сводится к следующим этапам:

1)     определение матрицы D по желаемым отрицательным собственным значениям;

2)     задание произвольной матрицы G, отличной от нулевой матрицы соответствующего порядка;

3)     решение уравнения Ляпунова (7.5) для нахождения матрицы L;

4)     решение исходного уравнения для заданного управления U(t). Определение Y(t) = CX(t);

5)     решение уравнения наблюдателя (7.3) или вычисление Z(t) по соотношению (7.4);

6)     определение матрицы Р;

7)     определение оценки вектора состояния исходной системы по соотношению (7.9).

Матрицу D всегда можно взять как сопровождающую (каноническую, матрицу Фробениуса) для характеристического полинома, который будет определяться по известным желаемым корням (расположенным в левой полуплоскости комплексной плоскости корней).

При структурном моделировании для оценки вектора состояния требуется знать вектор выхода исходной системы и вектор переменных состояния наблюдателя пониженного порядка.

Схема моделирования системы управления с наблюдателем пониженного порядка по соотношениям (7.11) – (7.15) показана на рис. 7.1.

Рис. 7.1. Схема объекта управления с наблюдателем пониженного

порядка