Анализ систем управления, заданных в пространстве состояний
Цель работы: освоить встроенные функции системы MATLAB для анализа линейных стационарных систем управления, заданных в пространстве состояний.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Многие системы управления
являются многомерными, для них характерно
наличие нескольких входов и выходов.
Описание систем во временной области
связано с понятием пространства
состояний. Состояние
системы – это
совокупность таких переменных, знание
которых наряду с входными функциями и
уравнениями, описывающими динамику
системы, позволяет определить ее будущее
состояние и выходную переменную [3]. Для
динамической системы ее состояние
описывается набором переменных
состояния 
которые
определяют будущее поведение системы,
если известны ее текущее состояние и
все внешние воздействия.
Состояние системы описывается дифференциальными уравнениями первого порядка относительно каждой из переменных состояния. Для линейных стационарных систем управления уравнения состояния в общем случае имеют следующий вид:
(2.1)
где 
–
функции независимого переменного t (времени).
Систему (2.1) можно записать в матричной форме
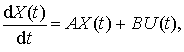(2.2)
где
–
вектор состояния размера n×1,
–
вектор управления размера r×1,
–
матрица состояний объекта размера n×n,
–
матрица входа размера n×r.
Векторное уравнение (2.2) часто называют уравнением состояния, которое связывает скорость изменения состояния системы с самим состоянием и управлением (входным воздействием).
В общем случае выходные переменные системы связаны с переменными состояниями и входными воздействиями (управлениями) алгебраическим уравнением выхода
(2.3)
где
–
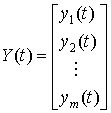вектор выхода размера m×1, m ≤ n,
–
матрица выхода размера m×n,
–
матрица обхода размера m×r.
Описание системы управления в пространстве состояний принято представлять в следующем виде:
(2.4)
(2.5)
Когда описание системы управления дано в виде (2.4), (2.5), систему можно исследовать на управляемость и наблюдаемость. Для этого достаточно применить критерии Калмана [18, 19].
А) Критерий полной управляемости системы по состоянию:
(2.6)
где n – размерность исследуемой системы.
Если выполняется условие (2.6), то система (2.4) полностью управляема по состоянию (по всем переменным состояния).
В) Критерий полной управляемости по выходу:
(2.7)
где m – размерность вектора выхода системы.
Если выполняется условие (2.7), то система (2.4), (2.5) полностью управляема по выходу (2.5).
С) Критерий полной наблюдаемости системы:
(2.8)
где n – размерность исследуемой системы.
Если выполняется условие (2.8), то система (2.4), (2.5) полностью наблюдаема.
Описание объектов управления с помощью передаточных функций
Цель работы: освоить методы описания объектов и систем управления в терминах «вход-выход» через передаточные функции и их анализ с помощью встроенных функций системы MATLAB.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Передаточная функция линейной стационарной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные условия равны нулю [1, 3, 9, 18, 19].
В соответствии с определением можно записать:
где Y(s) – изображение выходной переменной данной системы (объекта), W(s) – передаточная функция, U(s) – изображение входной переменной (управления), s – комплексная переменная.
Схемное изображение объектов (систем), заданных с помощью передаточных функций, показано на рис. 3.1.
Передаточная функция в общем случае является дробно рациональной относительно оператора преобразования Лапласа:
(3.1)
Условие m n отвечает условию реализуемости систем.
Преобразование Лапласа (прямое преобразование) имеет следующий вид:
(3.2)
где F(s) – функция комплексного переменного s, f(t) – функция действительного переменного t (времени), L – символ преобразования Лапласа.
Функцию F(s) называют изображением по Лапласу, функцию f(t) – оригиналом. Соотношение (3.2) устанавливает соответствие между изображением и оригиналом.
Передаточную функцию определяют также формально в операторной форме, когда символ дифференцированияd/dt заменяется на символ s (или p), что следует из свойства преобразования Лапласа: производная от оригинала соответствует умножению комплексной переменной на изображение данного оригинала.
Для системы управления, заданной в стандартной форме уравнений состояния
(3.3)
где X(t) – n-мерный вектор состояния, U(t) – r-мерный вектор управления, Y(t) – m-мерный вектор выхода, r ≤ n, m ≤ n, найдем общий вид передаточной функции.
Преобразование по Лапласу уравнений (3.3) при нулевых начальных условиях дает
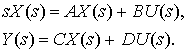(3.4)
Первое уравнение в (3.4) можно привести к виду
(3.5)
где Е – единичная матричная функция, и решить относительно X(s):
(3.6)
Подставляя (3.6) во второе уравнение (3.4), получим
(3.7)
Производя отношение выхода к входу, будем иметь следующий вид передаточной функции:
(3.8)
где W(s) есть в общем случае многомерная передаточная функция размера m×r, т. е.
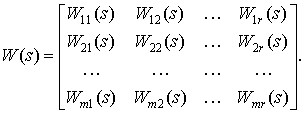(3.9)
Когда имеем один вход (r = 1) и один выход (m = 1) данной системы управления (система SISO – Single Input, SingleOutput), получим одномерную передаточную функцию. Многомерную систему принято обозначать как MIMO (MultipleInput, Multiple Output). Обычно матрица D в описании систем управления отсутствует. Тогда она формальна и должна быть нулевой матрицей соответствующего размера. При нулевой матрице D выражение (3.8) приобретает следующий вид:
(3.10)
В следующем разделе рассмотрим формирование одномерных и многомерных передаточных функций в системеMATLAB.