3. Критерий устойчивости найквиста

 

Частотный критерий устойчивости, разработанный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой динамической системы управления по виду амплитудно-фазовой характеристики разомкнутой системы [1, 9, 14, 21, 22].

Пусть передаточная функция разомкнутой системы имеет вид

 (10.15)

Выражение

 (10.16)

представляет собой характеристическое уравнение разомкнутой системы управления (10.15).

Подставляя в (10.15)  , получим частотную передаточную функцию разомкнутой системы:

 (10.17)

где   – действительная и мнимая части частотной передаточной функции;   – модуль и фаза частотной передаточной функции, которые определяются по формулам

 (10.18)

Если изменять частоту  от – до +, то вектор   будет меняться по величине и по фазе. Кривую, описываемую концом этого вектора в комплексной плоскости, называют амплитудно-фазовой характеристикойразомкнутой системы, или годографом Найквиста.

Амплитудно-фазовая характеристика (АФХ) симметрична относительно вещественной оси, поэтому можно вычерчивать только ту ее часть, которая соответствует положительным частотам  > 0.

Если объект управления с передаточной функцией   замкнуть отрицательной единичной обратной связью, то получим передаточную функцию замкнутой системы:

где   – характеристический полином замкнутой системы.

Рассмотрим вспомогательную функцию   С учетом (10.15) будем иметь

 (10.19)

где   – характеристическая кривая разомкнутой системы,

 – характеристическая кривая замкнутой системы.

Обозначим 

3.1. Критерий устойчивости найквиста в случае устойчивой разомкнутой системы

 

Если разомкнутая система управления устойчива, то изменение аргумента при возрастании частоты  от 0 до +будет равно [14]:

 (10.20)

где n – степень характеристического уравнения (10.15) разомкнутой системы.

Степень характеристического уравнения разомкнутой системы совпадает со степенью характеристического уравнения замкнутой системы, так как в реальных системах степень числителя передаточной функции не может превосходить степень знаменателя [14].

Изменение аргумента характеристической кривой замкнутой системы   при возрастании частоты  от 0 до + в общем случае равно

 (10.21)

где р – число корней характеристического уравнения  , лежащих в правой части комплексной плоскости.

Изменение аргумента вспомогательной функции (10.19) при возрастании частоты  от 0 до + равно разности изменений аргумента   и  , т. е.

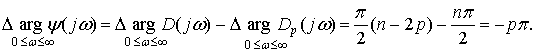
Замкнутая система будет устойчивой, если число правых корней равно нулю (р = 0), т. е. если

 (10.22)

Вектор   опишет угол, равный нулю, лишь в том случае, когда его годограф не охватывает начало координат. Поскольку вектор   отличается от вектора   разомкнутой системы на единицу (см. 10.19), то от кривой   можно перейти к амплитудно-фазовой характеристике (АФХ) разомкнутой системы  , если сместить кривую   на единицу влево.

Формулировка Критерия устойчивости Найквиста в случае устойчивой разомкнутой системы: замкнутая система автоматического управления будет устойчивой, если АФХ разомкнутой системы   не охватывает точки с координатами (–1, j0).