3. Фазовая частотная характеристика
Аргумент 
называют
фазовой частотной функцией, а ее график
– фазовой частотной характеристикой
(фазочастотной характеристикой).
Фазочастотная характеристика (ФЧХ) показывает фазовые сдвиги, вносимые звеном на различных частотах [1].
Выражение для фазовой частотной функции может быть получено из алгебраической формы записи частотной функции (9.3):
(9.6)
При вычислении 
по
формуле (9.6) значение k определяют,
исходя из каких-либо дополнительных
соображений, учитывая, что главные
значения функции тангенса терпят разрыв
2-го рода в точках (–/2)
и (/2).
В случае, когда фазовый сдвиг лежит в пределах [-π; π], можно воспользоваться следующей схемой расчета [12]:
(9.7)
При построении логарифмической
фазовой частотной характеристики (ЛФЧХ)
отсчет углов 
идет
по оси ординат в обычном масштабе в
угловых градусах. По оси абсцисс
откладывается по-прежнему частота в
логарифмическом масштабе.
Частотные критерии устойчивости линейных непрерывных систем управления
Цель работы: изучить критерии устойчивости Михайлова и Найквиста для непрерывных линейных стационарных систем управления; проанализировать устойчивость систем по логарифмическим частотным характеристикам.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Частотные критерии устойчивости в большинстве случаев используют в качестве графоаналитических критериев, так как они отличаются наглядностью при выполнении инженерных расчетов [9].
В основе частотных методов определения устойчивости систем управления лежит принцип аргумента – следствие теоремы Коши относительно числа нулей и полюсов функции, аналитической в заданной области [9].
1. Принцип аргумента
Пусть задано алгебраическое уравнение n-й степени с действительными коэффициентами:
(10.1)
Если 
–
корни уравнения (10.1), то алгебраический
полином 
можно
представить в виде
(10.2)
На комплексной плоскости
каждому корню соответствует вполне
определенная точка. Геометрически
каждый корень 
изображается
в виде вектора, проведенного из начала
координат комплексной плоскости к
точке
.
Длина этого вектора равна модулю
комплексного числа, т. е. 
,
а угол, образованный вектором с
положительным направлением действительной
оси, аргументу или фазе комплексного
числа
,
т. е. 
(см.
рис. 10.1). Векторы 
входящие
множителями в (10.2), проведены из точек
к
точке 
.
Каждый из этих векторов является
разностью двух векторов,
соответствующих
и
(см.
рис. 10.2).
Рис. 10.1. Модуль и фаза вектора
Рис. 10.2. Пример элементарного
вектора 
Если принять 
в
(10.2), то
(10.3)
где – круговая частота.
Концы элементарных
векторов 
будут
находиться на мнимой оси в точке
(см.
рис. 10.3).
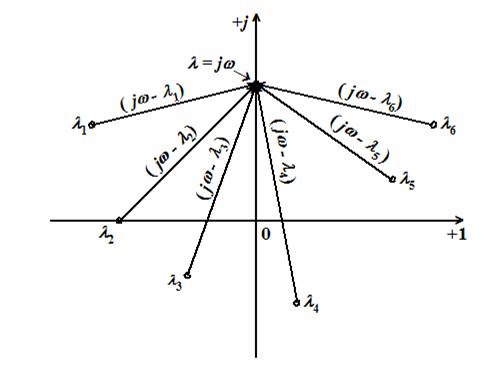
Рис. 10.3. Пример расположения элементарных векторов (j – i)
Модуль 
равен
произведению модулей элементарных
векторов
и
:
(10.4)
Аргумент или фаза равна сумме аргументов элементарных векторов:
(10.5)
На комплексной плоскости
за положительное направление примем
вращение вектора против часовой стрелки.
Тогда при изменении угловой частоты от
– до
+ каждый
элементарный вектор (j – i)
повернется на угол +,
если его начало (корень
)
лежит в левой части комплексной плоскости,
и на угол –,
если его начало (корень 
)
лежит в правой части комплексной
плоскости (см. рис. 10.4).
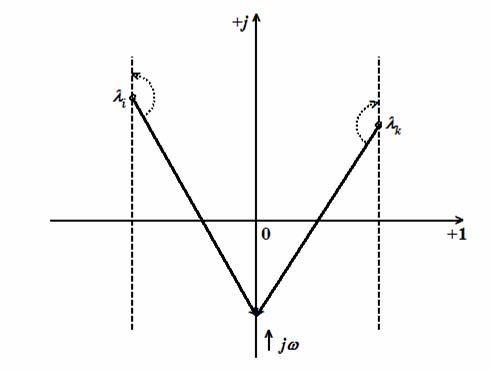
Рис. 10.4. Пример изменения аргумента вектора (j – i) и (j – k)
при возрастании частоты от – до +
Пусть уравнение (10.1), т. е. D() = 0 имеет р корней в правой части комплексной плоскости и, следовательно, (n –р) корней лежат в левой части комплексной плоскости корней. Тогда при возрастании частоты от – до + изменение аргумента вектора или угол поворота (равный сумме изменений аргументов элементарных векторов) будет определяться в виде
(10.6)
Из соотношения (10.6) следует, что изменение аргумента при возрастании от – до + равно разности (n– р) корней уравнения D() = 0, лежащих в левой части плоскости, и числом p корней уравнения, лежащих в правой части плоскости, умноженной на .
Соотношение (10.6) называется принципом аргумента.