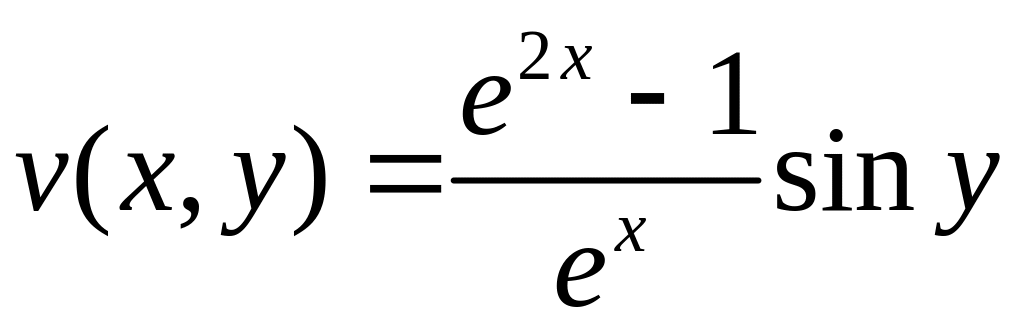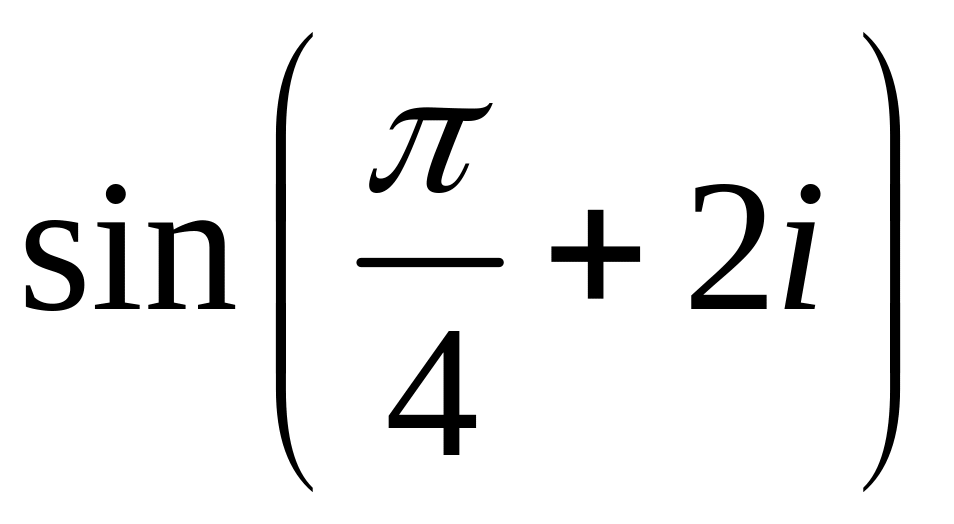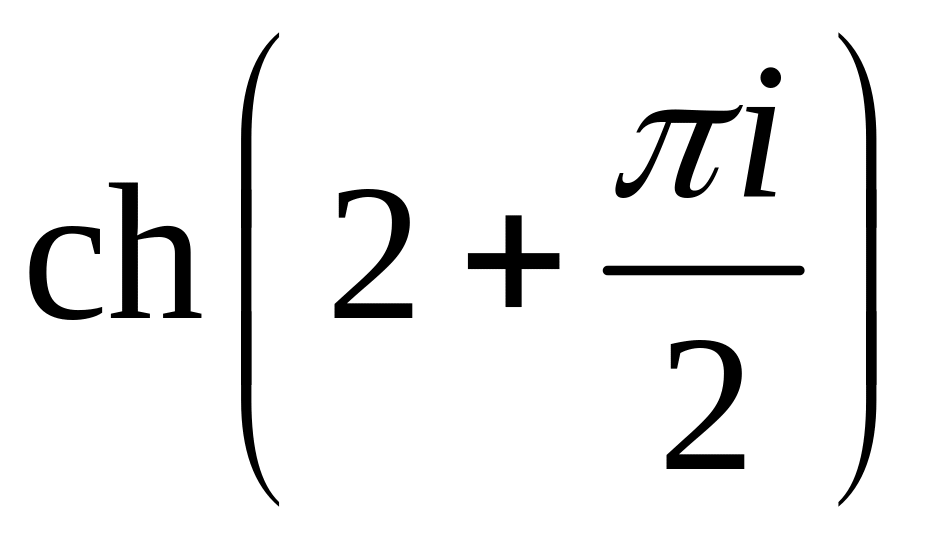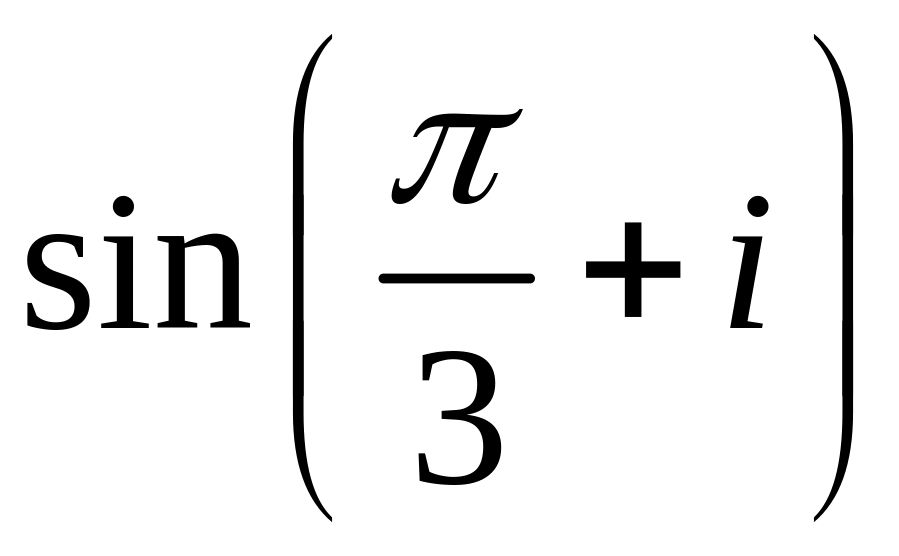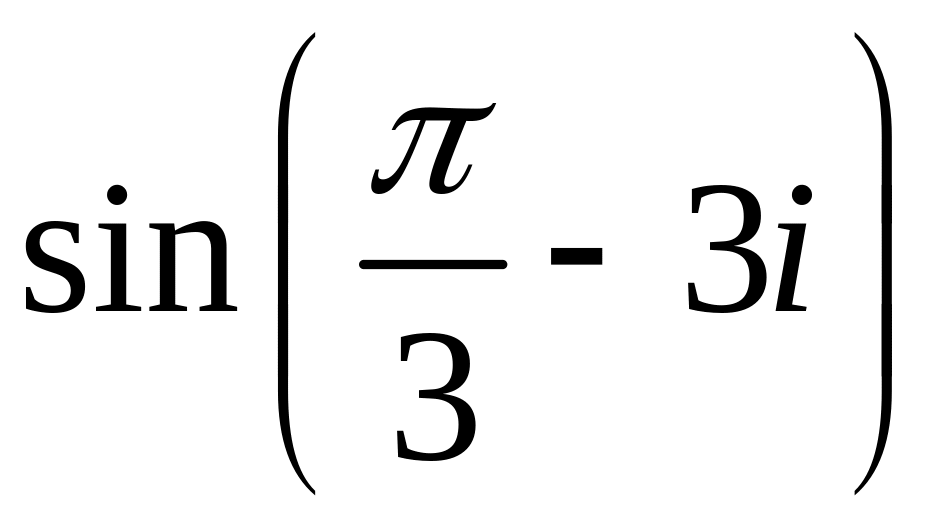МІНІСТЕРСТВО ОСВІТИ, НАУКИ, МОЛОДІ І СПОРТУ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ

імені ЮРІЯ КОНДРАТЮКА

Кафедра комп’ютерних та інформаційних технологій і систем

МАТЕМАТИЧНІ ОСНОВИ ЦИФРОВОЇ ОБРОБКИ СИГНАЛІВ

Індивідуальні завдання

для студентів заочної форми навчання

Напрям підготовки (спеціальність) 6.050102 Комп’ютерна інженерія

Укладач:

ст. викладач Руденко О.А.

Полтава

2011

Індивідуальне завдання № 1

За допомогою функції відобразити на площину лінію .

1.	, .	2.	, .
3.	, .	4.	, .
5.	, .	6.	, .
7.	, .	8.	, .
9.	, .	10.	, .
11.	, .	12.	, .
13.	, .	14.	, .
15.	, .	16.	, .
17.	, .	18.	, .
19.	, .	20.	, .
21.	, .	22.	, .
23.	, .	24.	, .
25.	, .	26.	, .
27.	, .	28.	, .
29.	, .	30.	, .

Приклад. За допомогою функції відобразити на площину лінію .

Розв’язання. .

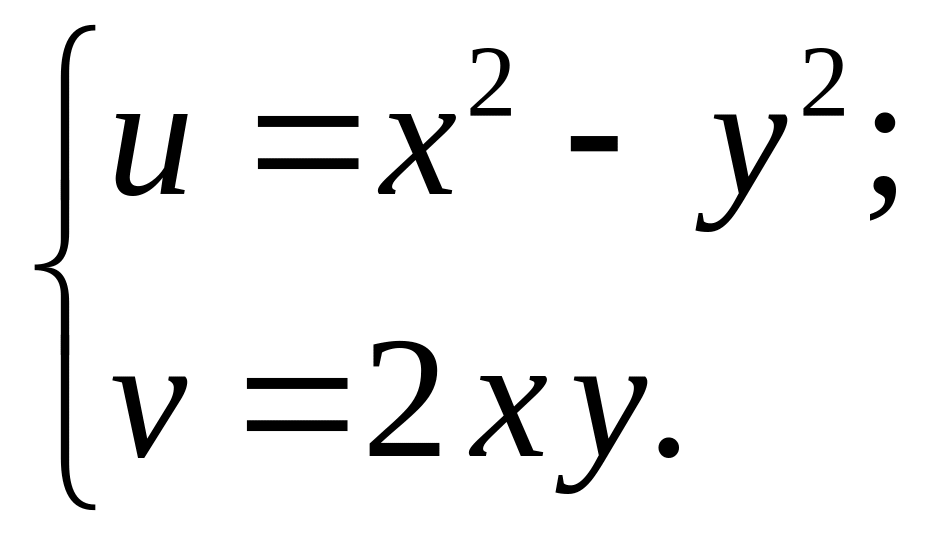
З одержаних рівнянь виключимо і .

.

Отже, відображенням прямої на площину є парабола .

Індивідуальне завдання № 2

Довести, що функція є гармонійною і відновити за відомою дійсною (уявною ) частиною функцію з точністю до довільної сталої.

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Приклад. Довести, що функція є гармонічною і відновити за відомою дійсною частиною функцію з точністю до довільної сталої

.

Розв’язання. Функція є гармонічною, якщо вона задовольняє рівняння Лапласа

.

, ,

, .

.

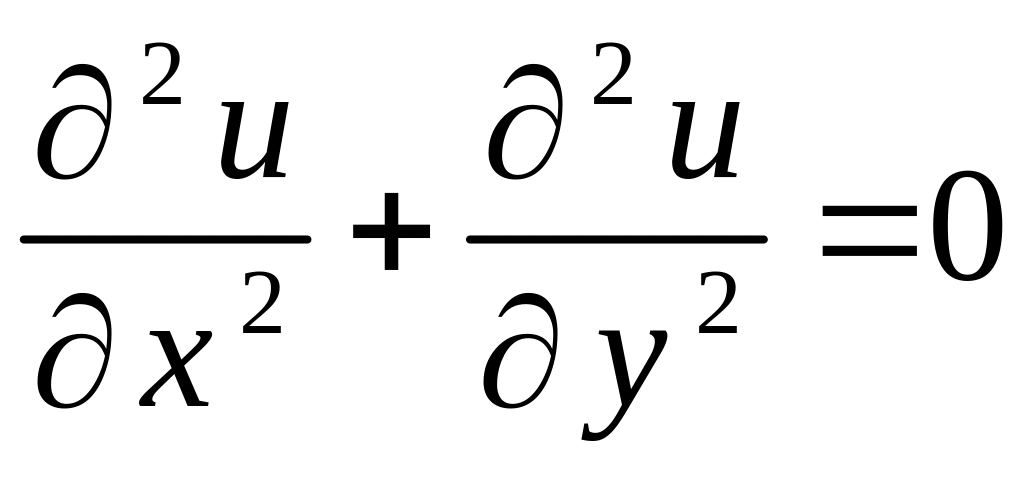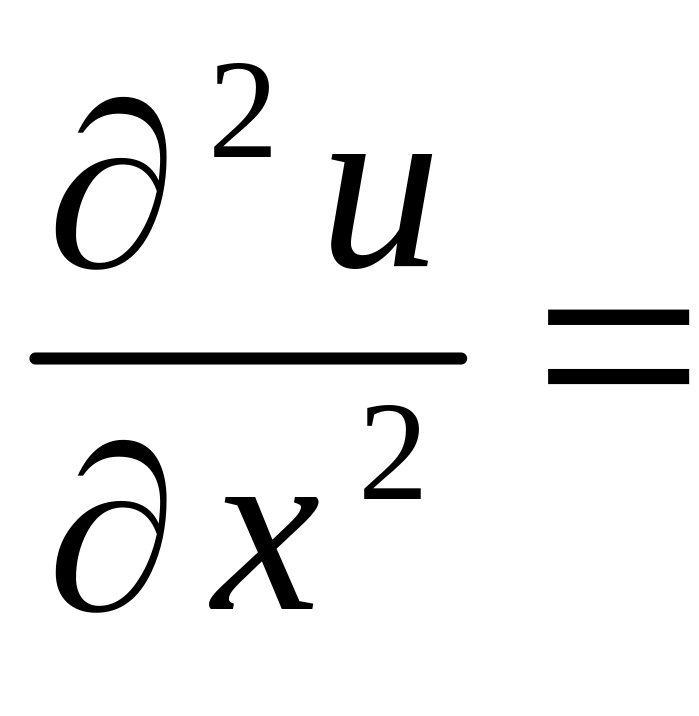
Отже, функція гармонійна.

Для знаходження уявної частини функції використаємо умови Коші-Рімана

, .

Маємо . За першою з умов Коші-Рімана , отже, . Звідси . Продиференціюємо по і використаємо другу з умов Коші-Рімана.

Отже, .

.

Відповідь: .

Індивідуальне завдання № 3

Подати в алгебраїчній формі

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Приклад. Обчислити значення заданих функцій у вказаних точках

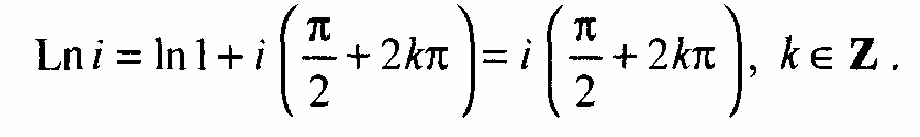
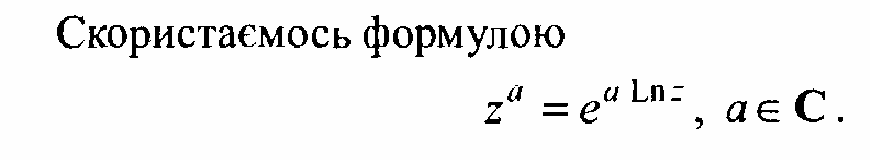
Індивідуальне завдання № 4

Знайти

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Обернені тригонометричні та параболічні функції на всій комплексній площині визначаються наступним чином:

, ,

, , , , , .

Приклад. Знайти .

Розв’язання. Використаємо формули:

, ,

, враховуючи, що радіус-вектор комплексного числа знаходиться у другій чверті, .

Маємо, ,

.

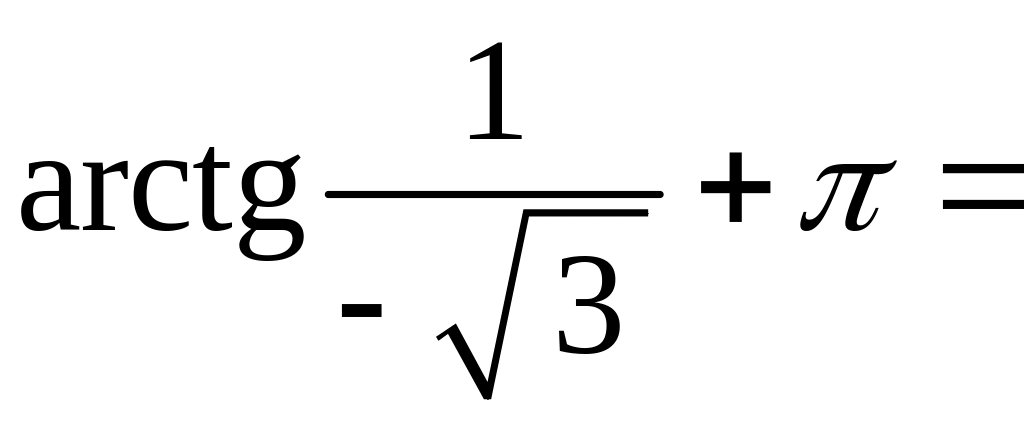
Отже, , .

Відповідь: , .

Приклад. Знайти .

Розв’язання. Використаємо формулу .

.

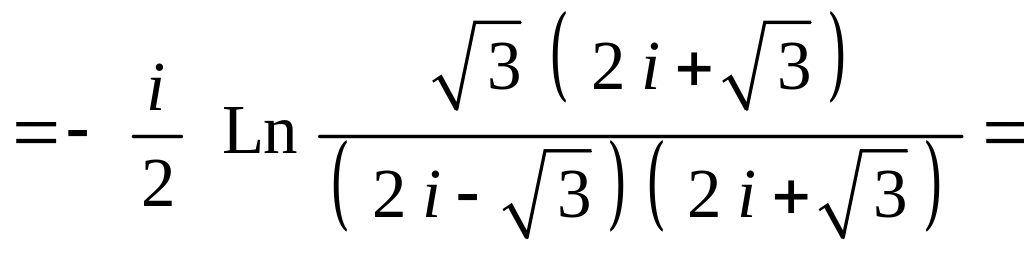
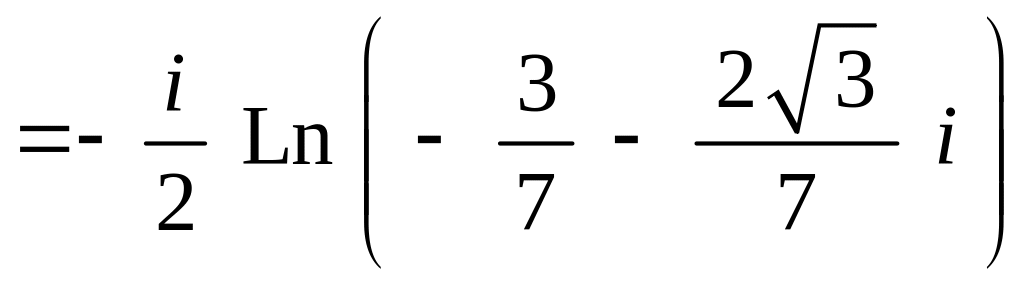, враховуючи, що радіус-вектор комплексного числа 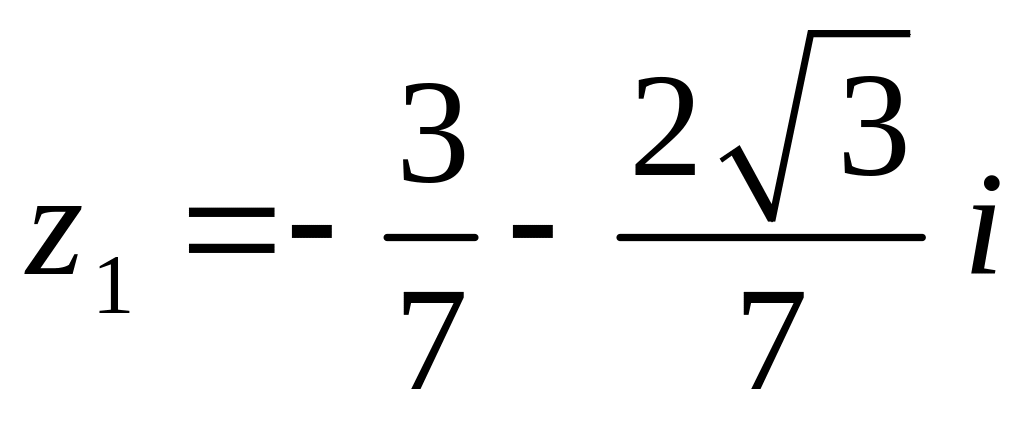знаходиться у третій чверті, .

,

.

, .

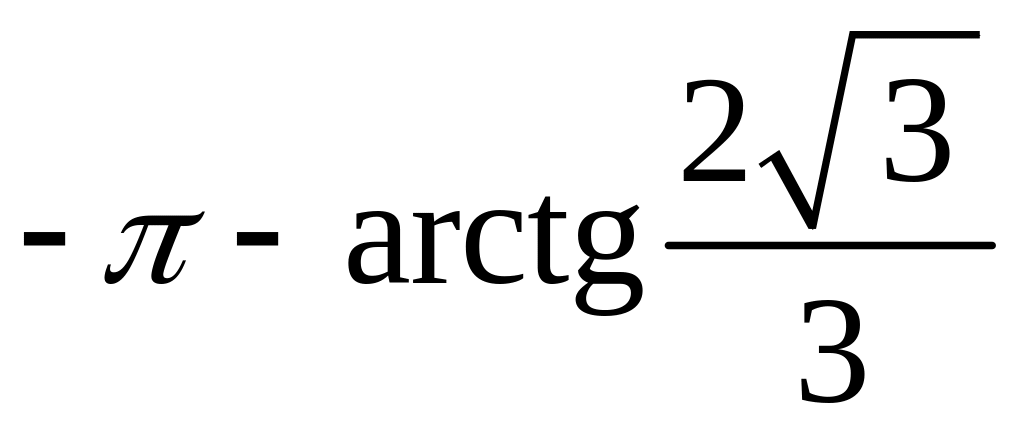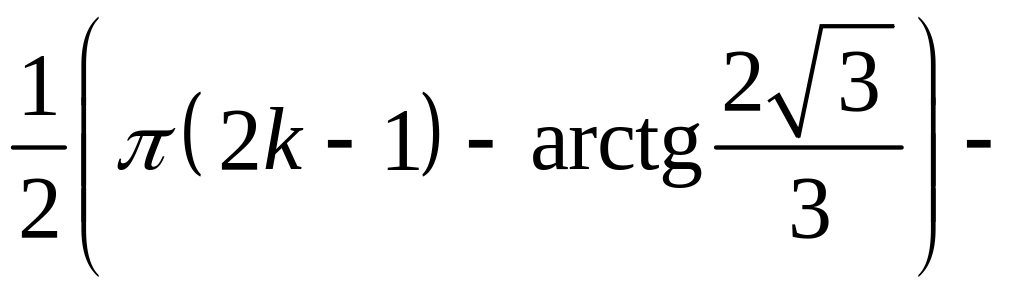
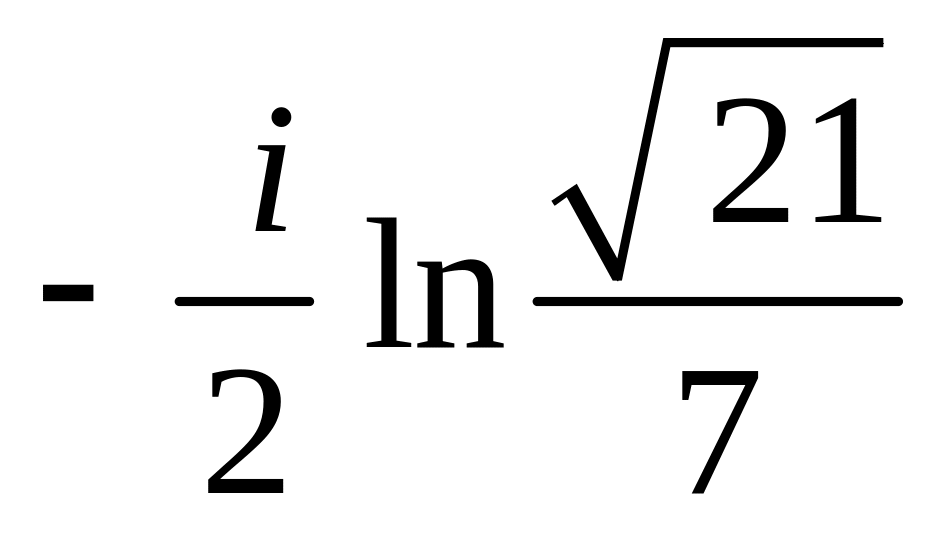Відповідь: , .

Приклад. Знайти .

Розв’язання. Використаємо формулу .

.

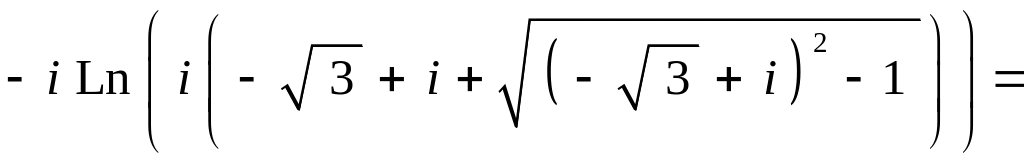
Знайдемо .

Використаємо формулу , .

,

.

. ;

. .

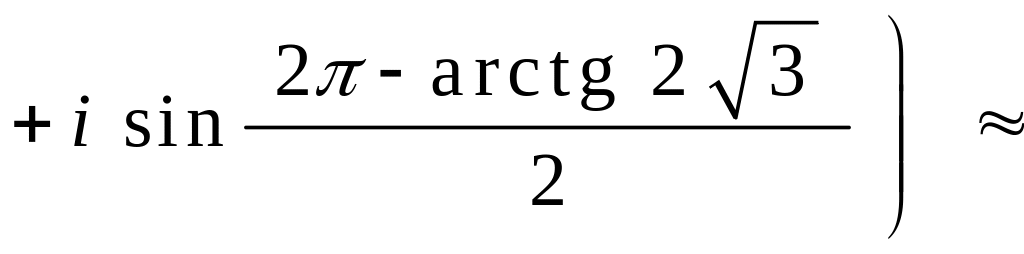
При знаходженні використана парність косинуса і непарність синуса.

.

,

.

, .

.

,

.

, .

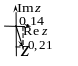
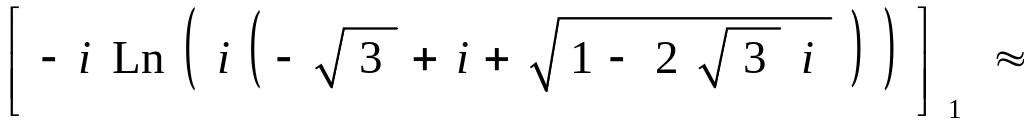
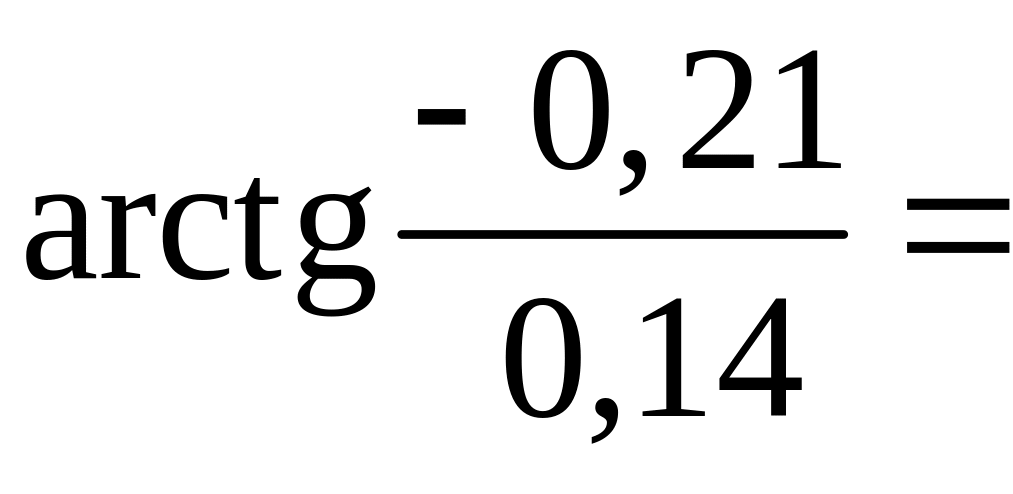
Відповідь: , ; , .