1.3 Расчёт частотной зависимости характеристического сопротивления фильтра
При Rг = Rн=500 Ом значение номинального характеристического сопротивления целесообразно принять одинаковым на входе и выходе фильтра и равным сопротивлению нагрузки, так как на входе и выходе схемы могут располагаться полузвенья с разным характеристическим сопротивлением Zтm и Znm.
Расчёты ведутся по формулам.
Расчётные данные занесены в таблицу 4.
Таблица 4
Омега |
Zпк |
Zтм |
0 |
500,00 |
500,00 |
0,1 |
502,52 |
500,70 |
0,2 |
510,31 |
502,77 |
0,3 |
524,14 |
506,12 |
0,4 |
545,54 |
510,54 |
0,5 |
577,35 |
515,49 |
0,6 |
625,00 |
519,75 |
0,7 |
700,14 |
520,21 |
0,75 |
755,93 |
516,75 |
0,8 |
833,33 |
508,13 |
0,825 |
884,75 |
500,65 |
0,85 |
949,16 |
489,94 |
0,875 |
1032,80 |
474,63 |
0,9 |
1147,08 |
452,54 |
0,925 |
1315,90 |
419,95 |
0,95 |
1601,28 |
369,61 |
0,975 |
2250,18 |
283,71 |
1 |
1E+12 |
0 |
По данным таблицы строятся графики частотной зависимости характеристического сопротивления фильтра.
График 3
Коэффициент использования полосы пропускания фильтра.
Коэффициент использования полосы пропускания фильтра К1 найдём по следующей формуле:
, где S=
= 0,71
= 0.997
f1 = fср * K1 = 2500*0,997 = 2492,5 Гц
2. Расчет корректора фазочастотной характеристики тракта передачи сигналов
Исходные данные:
Вид корректируемой цепи - ФНЧ
Сопротивление нагрузок - Rг=Rн= 500 Ом
Полоса частот - 100-0,8*fср Гц
Допустимое отклонение результирующего фазового сдвига тракта передачи и корректора не более - 16 град.
Отклонение ёмкости конденсаторов, применяемых в схемах, от номинального значения не более - 5%
2.1 Определение требуемой частотной характеристики фазового сдвига корректора
Требуется
скорректировать ФЧХ ФНЧ в диапазоне
частот fн
=100.. fb=
2000, (bk.
– bтрk)
16
, то есть при
от 0,04 до 0,8.
н=f/fср=100/2500=0,04 в=f/fср=0,8*fср/fср=0,8
По данным таблицы 3 строим зависимость фазового сдвига звеньев bф=3,5*bк+.bm в расситанном выше диапозоне.(График 4)
На графике видно, что bкор.тр. max < 180 (П), следовательно, выбираем схему корректора первого порядка.
Принципиальная схема корректора.
Рис.4
Реальная характеристика bƩ=bф+bкор=k*Ω
Отсюда, bкор.тр.= k*Ω-bф.
На Графике 4 проводим прямую k* Ω - идеальная характеристика, а затем строим кривую bкор.тр. - требуемая частотная характеристика фазового сдвига корректора.
Таблица 5
bф |
Омега |
k |
k*Омега |
bкор |
bсумм |
bкор.тр. |
∆b |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,28 |
0,57 |
0,07 |
0,07 |
0,0049 |
0,028133 |
0,598133 |
-0,5651 |
0,28 |
1,15 |
0,14 |
0,14 |
0,0196 |
0,056254 |
1,206254 |
-1,1304 |
0,28 |
1,74 |
0,21 |
0,21 |
0,0441 |
0,084353 |
1,824353 |
-1,6959 |
0,28 |
2,33 |
0,28 |
0,28 |
0,0784 |
0,112419 |
2,442419 |
-2,2516 |
0,28 |
2,94 |
0,35 |
0,35 |
0,1225 |
0,140441 |
3,080441 |
-2,8175 |
0,28 |
3,58 |
0,42 |
0,42 |
0,1764 |
0,168407 |
3,748407 |
-3,4036 |
0,28 |
4,24 |
0,49 |
0,49 |
0,2401 |
0,196308 |
4,436308 |
-3,9999 |
0,28 |
4,93 |
0,56 |
0,56 |
0,3136 |
0,224132 |
5,154132 |
-4,6164 |
0,28 |
5,68 |
0,63 |
0,63 |
0,3969 |
0,25187 |
5,93187 |
-5,2831 |
0,28 |
6,49 |
0,7 |
0,7 |
0,49 |
0,27951 |
6,76951 |
-6 |
0,28 |
7,41 |
0,77 |
0,77 |
0,5929 |
0,307043 |
7,717043 |
-6,8171 |
0,28 |
8,48 |
0,84 |
0,84 |
0,7056 |
0,33446 |
8,81446 |
-7,7744 |
0,28 |
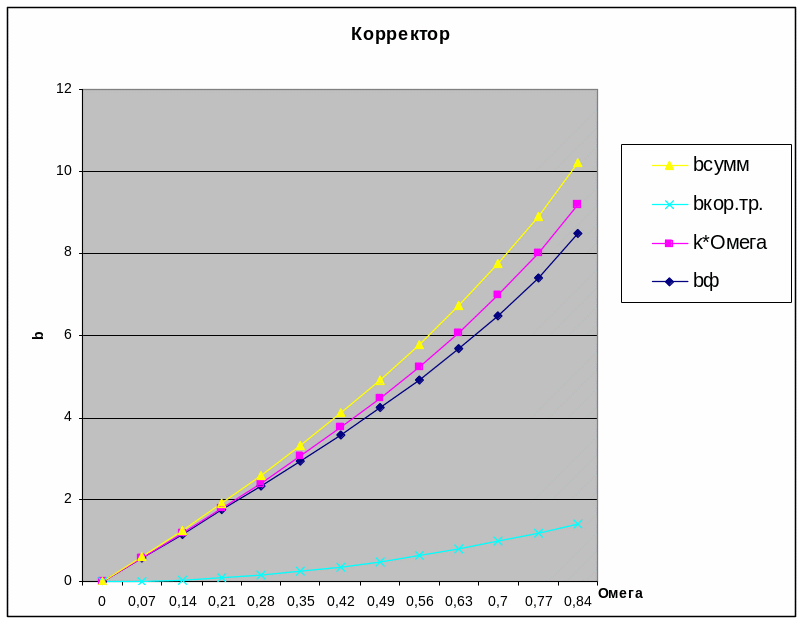
График 4
Рассчитаем параметры элементов схемы корректора первого порядка, представленного на рис.4.
Для этого графически находим значение bкор.тр. при относительной частоте Ω1=0,21:
b1=bкор.тр.(Ω1=0,21)=2*arctg(x1/R)=2*arctg((w*L)/R)=| Ω=w/wср;w= Ω*wср=2*П*fср* Ω|=2*arctg((2*П*fср* Ω*L)/R)=0,84(рад)
L=tg(b1/2)*R/П*fср=0,39*500/3,14*2500=0.025(Гн)
C=L/R^2=0,025/250000=0,0000001=0,1(мкФ)