Задача 2.

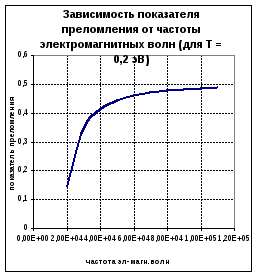
Используя данные полученные в результате расчета первой задачи построить зависимость показателя преломления и коэффициента поглощения плазмы от частоты электромагнитных волн в области частот–

от _p – до 510¹⁴ Hz. Не учитывать вклад подвижности ионов в диэлектрическую проницаемость плазмы. Зависимости построить для трех значений температуры плазмы

0.3, 1.5, 3 eV.

Немного теории.

Рассмотрим диэлектрическую проницаемость и распространение волн в средах со свободными зарядами

Примерами сред, содержащих свободные заряды, могут слу­жить металлы и плазма.

Типичная плазма — это частично или пол­ностью ионизованный газ. Плазмой также называют

и электронный газ (или электронную жидкость) в полупроводниках и металлах.

Однако в дальнейшем будет идти речь, в основном, о газовой плазме. Для вы­яснения

особенностей распространения волн в плазме необходимо найти зависимость ее

диэлектрической проницаемости от частоты.

Рассмотрим наиболее простую модель, дающую достаточно хорошее согласие с экспериментом. Будем считать среду квази­нейтральной и пренебрежем тепловым движением частиц. При этом в поле электромагнитной волны волны будет происходить лишь упорядоченное движение заряженных частиц.

Пусть в единице объема среды содержится N свободных электронов и такое же количество однократно заряженных положи­тельных ионов. Поскольку масса иона М во много раз больше массы электрона m, то в первом приближении движением ионов можно пренебречь. Неподвижные ионы образуют положительный заряд, а электроны свободно движутся под действием поля волны, испытывая при этом соударения остальными частицами плазмы .

Уравнение движения для электрона имеет вид:

Здесь Е — среднее макроскопическое поле; в отличие от диэлек­триков, при изучении плазмы можно считать, что действующее поле примерно равно макроскопическому: _Е_Д Е,

 -это эф­фективная частота соударений электронов с ионами и нейтраль­ными атомами и молекулами.

При гармонической зависимости поля от времени E~ехр(-it) имеем:

,

Поскольку плотность тока смещения равна j = = = -iP, не­трудно получить для удельной поляризации среды (единицы обьема):

Если учесть также смещение ионов в поле волны, то в выражение для поляризации войдет еще один член:

Однако вклад от ионов в поляризацию среды является лишь малой поправкой порядка т/M ~ 10~³, и его можно не учитывать. Поэтому

где _p =( 4е²N_e /т_e)^1/2 — плазменная или ленгмюровская частота колебаний электронного газа.

Известно, что, мнимая часть диэлектрической проницае­мости эквивалентна проводимости среды. Поэтому

Для металлов при частотах волны  <10¹⁰ с^-1 реализуются соотношения _p >>, >>; проводимость является действительной величиной:

 = Ne²/mv, не зависящей от частоты, а диэлектри­ческая проницаемость, - мнимой. Например, для меди N 8 10²¹ см^-3 , 3 10¹³ с^-1 и  5107 Ом^-м^-1 вплоть до инфракрасной области спектра. В этом диапазоне частот показатель преломления и показатель поглощения примерно равны п = к = . Поле существует только в скин-слое, толщина которого d = (kn)^-1 << Коэффициент отражения от поверхности металла близок к единице.

При более высоких частотах диэлектрическая проницаемость комплексна и существенным образом зависит от частоты. При > металл становится прозрачным

В разреженной плазме (например, в ионосфере) эффективная частота соударений  ~ 10³—10⁴ с-¹ и для волн с частотой f >10⁶ с-¹ выполняется условие >> В этом случае мнимой частью диэлектрической прони­цаемости можно пренебречь и

(2.1)

Закон дисперсии определяется соотношением

или

Если , то показатель преломления есть действительное число и волны свободно распространяются в среде. Если ,

то п = 0. При показатель преломления становится мни­мым, следовательно, волны при должны отражаться от границы плазмы.. Частота электромагнитной волны при которой происходит её отражение от слоя плазмы и равная плазменной частоте, называется критической - f_кр:

Заметим, что показатель преломления может обратиться в нуль или стать чисто мнимой величиной только в среде, в которой поглощение энергии пренебрежимо мало.

Рассмотрим поглощение волн в плазме, обусловленное столк­новениями электронов с молекулами и ионами (классическое). При этом необходимо различать два случая: поглощение при прохождении волны через слой плазмы (когда можно считать, что  > _р) и поглощение при отражении волны от слоя (когда   _р).

В первом случае, полагая в формуле (5.3) ² << ², > _р, получим

, ,

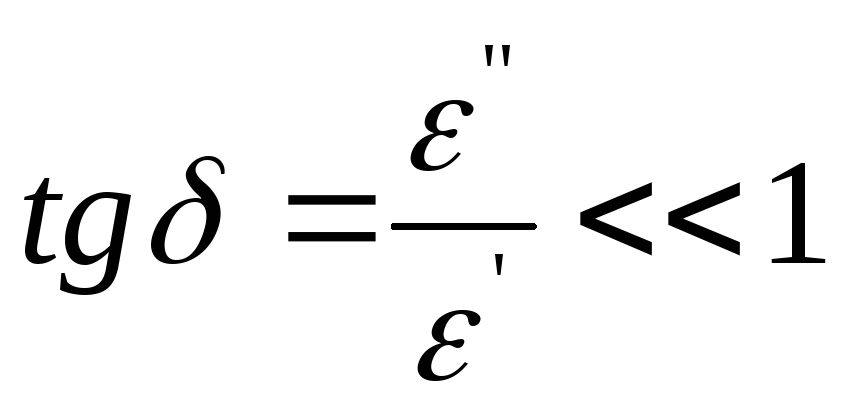
Показатель поглощения, (см. лекции Н.Н. Розанова) определяется формулой

Коэффициент поглощения при этом равен

(см^-1)

Как видно из приведенных выше формул для нахождения указанных в задаче зависимостей необходимо определить частоту столкновений электронов плазмы с тяжелыми частицами.

Частота столкновений электронов с ионами равняется

где сечение столкновения ,

параметр ближнего взаимодействия - ;

Кулоновский логарифм - ;

Средняя тепловая скорость электронов

, здесь T в eV, V_e – в см/сек, m_e- в г

Частота электронт-атомных столкновений:

, где , и - радиус атома водорода.

И наконец,

Таким образом, приведенные выше формулы полностью определяют возможность решения поставленной задачи.

Условие:

T Ni1 Ni2 Ne Na Rd Wp

0.2 8.9428E-02 -1.0506E-55 8.9428E-02 3.2000E+17 7.8601E+02 1.6872E+04

0.3 3.3024E+06 2.2261E-30 3.3024E+06 3.1999E+17 1.5841E-01 1.0252E+08

0.4 1.1408E+10 6.7700E-19 1.1408E+10 3.1999E+17 3.1122E-03 6.0262E+09

0.5 1.0504E+12 3.5762E-11 1.0504E+12 3.1999E+17 3.6262E-04 5.7825E+10

0.6 2.1960E+13 5.4266E-06 2.1960E+13 3.1997E+17 8.6877E-05 2.6439E+11

0.7 1.9605E+14 2.8246E-02 1.9605E+14 3.1980E+17 3.1405E-05 7.8999E+11

0.8 1.0251E+15 1.7781E+01 1.0251E+15 3.1897E+17 1.4682E-05 1.8064E+12

0.9 3.7383E+15 2.7292E+03 3.7383E+15 3.1626E+17 8.1552E-06 3.4496E+12

1.0 1.0533E+16 1.5565E+05 1.0533E+16 3.0946E+17 5.1210E-06 5.7906E+12

1.1 2.4409E+16 4.3142E+06 2.4409E+16 2.9559E+17 3.5283E-06 8.8147E+12

1.2 4.8321E+16 6.9524E+07 4.8321E+16 2.7167E+17 2.6192E-06 1.2402E+13

1.3 8.3646E+16 7.3760E+08 8.3646E+16 2.3635E+17 2.0720E-06 1.6317E+13

1.4 1.2846E+17 5.6307E+09 1.2846E+17 1.9153E+17 1.7351E-06 2.0221E+13

1.5 1.7698E+17 3.3015E+10 1.7698E+17 1.4301E+17 1.5301E-06 2.3735E+13

1.6 2.2155E+17 1.5615E+11 2.2155E+17 9.8445E+16 1.4124E-06 2.6556E+13

1.7 2.5649E+17 6.1859E+11 2.5650E+17 6.3500E+16 1.3531E-06 2.8574E+13

1.8 2.8054E+17 2.1132E+12 2.8054E+17 3.9457E+16 1.3313E-06 2.9883E+13

1.9 2.9570E+17 6.3714E+12 2.9571E+17 2.4290E+16 1.3322E-06 3.0681E+13

2.0 3.0486E+17 1.7269E+13 3.0490E+17 1.5116E+16 1.3461E-06 3.1153E+13

2.1 3.1033E+17 4.2717E+13 3.1042E+17 9.6177E+15 1.3670E-06 3.1434E+13

2.2 3.1361E+17 9.7608E+13 3.1381E+17 6.2848E+15 1.3916E-06 3.1605E+13

2.3 3.1556E+17 2.0810E+14 3.1598E+17 4.2219E+15 1.4180E-06 3.1715E+13

2.4 3.1666E+17 4.1741E+14 3.1750E+17 2.9129E+15 1.4450E-06 3.1791E+13

2.5 3.1714E+17 7.9298E+14 3.1873E+17 2.0605E+15 1.4720E-06 3.1852E+13

2.6 3.1707E+17 1.4345E+15 3.1994E+17 1.4913E+15 1.4983E-06 3.1913E+13

2.7 3.1641E+17 2.4819E+15 3.2137E+17 1.1022E+15 1.5234E-06 3.1984E+13

2.8 3.1504E+17 4.1202E+15 3.2329E+17 8.3023E+14 1.5468E-06 3.2079E+13

2.9 3.1278E+17 6.5786E+15 3.2594E+17 6.3618E+14 1.5677E-06 3.2210E+13

3.0 3.0938E+17 1.0119E+16 3.2962E+17 4.9507E+14 1.5856E-06 3.2392E+13

3.1 3.0459E+17 1.5014E+16 3.3462E+17 3.9059E+14 1.5997E-06 3.2637E+13

3.2 2.9817E+17 2.1508E+16 3.4119E+17 3.1187E+14 1.6096E-06 3.2956E+13

3.3 2.8997E+17 2.9776E+16 3.4952E+17 2.5156E+14 1.6150E-06 3.3355E+13

3.4 2.7990E+17 3.9891E+16 3.5968E+17 2.0458E+14 1.6159E-06 3.3837E+13

3.5 2.6802E+17 5.1804E+16 3.7163E+17 1.6740E+14 1.6129E-06 3.4394E+13

3.6 2.5451E+17 6.5345E+16 3.8520E+17 1.3756E+14 1.6067E-06 3.5017E+13

3.7 2.3964E+17 8.0245E+16 4.0013E+17 1.1329E+14 1.5982E-06 3.5689E+13

3.8 2.2373E+17 9.6167E+16 4.1607E+17 9.3361E+13 1.5884E-06 3.6393E+13

3.9 2.0718E+17 1.1273E+17 4.3266E+17 7.6876E+13 1.5780E-06 3.7111E+13

4.0 1.9035E+17 1.2957E+17 4.4951E+17 6.3184E+13 1.5678E-06 3.7827E+13

Решение:

1. показатель преломления рассчитывается по формуле:

причем: Wp соответствует заданной температуре (T = 0,2; 1,9; 4 эВ),

W выбирается в интервале [Wp – 5*10¹⁴]

Расчеты для построения графиков для 3х температур:

	T = 0,2 эВ	Wp=1,69E+04	Т = 1,9 эВ	Wp=3,07E+13	T = 4 эВ		Wp=3,78E+13
	W	n	W	n	W		n
	2,00E+04	0,14417	4,00E+13	2,06E-01	5,00E+13		0,213824
	3,00E+04	0,341853	5,00E+13	3,12E-01	6,00E+13		0,301266
	4,00E+04	0,411042	6,00E+13	3,69E-01	7,00E+13		0,353992
	5,00E+04	0,443067	7,00E+13	4,04E-01	8,00E+13		0,388212
	6,00E+04	0,460463	8,00E+13	4,26E-01	9,00E+13		0,411674
	7,00E+04	0,470953	9,00E+13	4,42E-01	1,00E+14		0,428456
	8,00E+04	0,477761	1,00E+14	4,53E-01	1,10E+14		0,440873
	9,00E+04	0,482428	1,10E+14	4,61E-01	1,20E+14		0,450317
	1,00E+05	0,485767	1,20E+14	4,67E-01	1,30E+14		0,457666
	1,10E+05	0,488237	1,30E+14	4,72E-01	1,40E+14		0,463498