Лабораторная работа №7
ИССЛЕДОВАНИЕ ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ С ПЕРИОДИЧЕСКИМИ НЕСИНУСОИДАЛЬНЫМИ ЭДС
Цель работы
Экспериментальная проверка расчета линейных электрических цепей при периодических воздействиях несинусоидальной формы.
Основные теоретические положения
В большинстве практических случаев форма периодических токов и напряжений в той или иной мере отличается от синусоидальной.
Источниками несинусоидальных напряжений могут быть различные генераторы несинусоидальных колебаний (например генераторы прямоугольных колебаний) или цепи, питающиеся от синусоидальных ЭДС и содержащие безынерционные нелинейные элементы (катушки индуктивности с ферромагнитными сердечниками, выпрямители, нелинейные конденсаторы и т. д.).
Расчет линейной цепи, к которой подводится несинусоидальное напряжение, производится методом наложения. Для этого периодическую несинусоидальную ЭДС представляют в виде последовательного соединения нескольких ЭДС кратных частот. Амплитудные значения и начальные фазы ЭДС определяются путем разложения несинусоидальной функции в тригонометрический ряд Фурье. Далее определяют ток от каждой гармонической составляющей ЭДС и, суммируя мгновенные значения токов гармоник, получают искомый ток, записанный в виде ряда Фурье.
Из курса математики известно, что периодическая функция, удовлетворяющая условиям Дирихле, может быть разложена в ряд Фурье:
![]() (7.1)
(7.1)
где
![]() -
постоянная составляющая;
-
постоянная составляющая;
![]() –первая
или основная гармоника.
–первая
или основная гармоника.
Все
последующие члены именуются по номеру
гармоники и носят названия высших
гармоник:
![]() -
высшая гармоника порядка К.
-
высшая гармоника порядка К.
Важно отметить, что постоянная, амплитуды и взаимное расположение гармоник не зависят от выбора начала координат, тогда как значения начальных фаз зависят от начала отсчета. Ряд Фурье может быть представлен и в другом виде:
![]() (7.2)
(7.2)
Переход от одной формы ряда Фурье к другой осуществляется при помощи соотношений
![]() (7.3)
(7.3)
Если функция f(t) задана аналитически, то коэффициенты членов ряда (7.2) могут быть определены по формулам
 (7.4)
(7.4)
В математических и электротехнических справочниках имеются таблицы с разложением в ряд Фурье многих периодических функций.
Выбор числа членов ряда определяется требуемой точностью расчетов. На практике достаточно использование первых четырех–пяти членов, так как ряд Фурье обладает быстрой сходимостью.
Расчет цепи производится для каждой гармоники в отдельности методами, применяемыми при расчете цепей синусоидального тока, с учетом того, что сопротивление реактивных элементов зависит от номера гармоники. Следует также иметь в виду, что результирующий ток (напряжение) получают путем суммирования мгновенных значений гармоник, а не соответствующих им комплексов.
Для оценки
действия периодически изменяющихся
токов и напряжений вводятся такие
величины, как максимальное значение за
период
![]() действующее
(среднеквадратичное значение за период):
действующее
(среднеквадратичное значение за период):
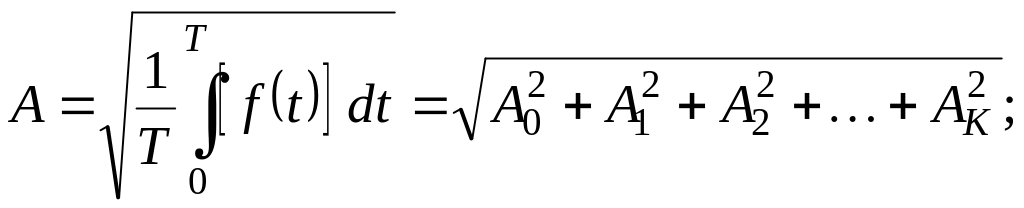
среднее значение за период:
![]()
и среднее по модулю за период:
![]()
Измерять мгновенное напряжение удобно с помощью электронного осциллографа, действующее напряжение приборами электромагнитной, электродинамической, тепловой систем. Приборы магнитоэлектрической системы реагируют на среднее значение измеряемой величины (постоянную составляющую),а электромагнитной с выпрямителем –– на среднее по модулю за период.
Показания электронных приборов определяются их назначением. Для оценки несинусоидальных периодических кривых без постоянной составляющей, т.е. симметричных относительно оси абсцисс, вводят следующие коэффициенты:
а) коэффициент формы, который определяется как отношение действующего значения к среднему по модулю значению функции:
![]()
б) коэффициент искажения – отношение действующего значения основной гармоники к действующему значению несинусоидальной функции:
![]()
c) коэффициент
амплитуды – отношение максимального
значения к действующему;
![]()
![]()
Значения
величин коэффициентов
![]() для типовых форм кривых приводятся в
справочной литературе.
для типовых форм кривых приводятся в
справочной литературе.
Активная мощность определяется как среднее значение мгновенной мощности за период:
![]()
или как сумма активных мощностей гармоник, т.е.
![]() .
.
В экспериментальной части работы проводится сравнение осциллограммы тока неразветвленной части цепи с графиком того же тока, построенного по расчетным данным. Исследуется влияние характера сопротивления элемента цепи на форму тока в нем.
Примеры расчета цепей при воздействии периодических несинусоидальных источников
Пример 9.1
Дано:
![]() ,
,
![]() ;
;
![]() Ом;
Ом;
![]() Ом;
Ом;
![]() Гн;
Гн;
![]() мкФ;
мкФ;
![]() Гн.
Гн.
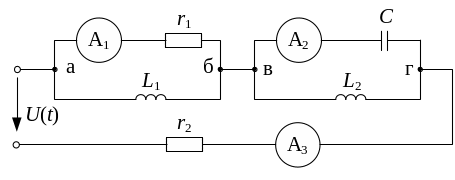
Определить показания амперметров, включённых в цепь схемы (рис. 9.5) и измеряющих действующие значения токов, а также активную, реактивную и полную мощности.
|
Рис. 9.5 |
Решение
Напряжение,
приложенное к цепи, представляет сумму
постоянной составляющей, первой и пятой
гармоник. Действие этого напряжения
аналогично действию трёх последовательно
соединённых источников напряжения
![]() В;
В;
![]() и
и
![]() .
Рассчитаем токи цепи при действии
каждого из этих источников в отдельности
(принцип наложения):
.
Рассчитаем токи цепи при действии
каждого из этих источников в отдельности
(принцип наложения):
1) Расчёт постоянной составляющей.
Определим
в каких ветвях цепи протекает постоянный
ток. Ветвь, содержащая ёмкость, для
постоянного тока равносильна разрыву
цепи, следовательно, по ней он протекать
не будет. Постоянный ток не будет также
протекать по сопротивлению
![]() ,
которое замыкается индуктивностью
накоротко
,
которое замыкается индуктивностью
накоротко
![]() .
Следовательно, постоянный ток протекает
по пути
.
Следовательно, постоянный ток протекает
по пути
![]() .
Расчётная схема для определения
постоянной составляющей представлена
на рис. 9.6.
.
Расчётная схема для определения
постоянной составляющей представлена
на рис. 9.6.
|
Рис. 9.6 |
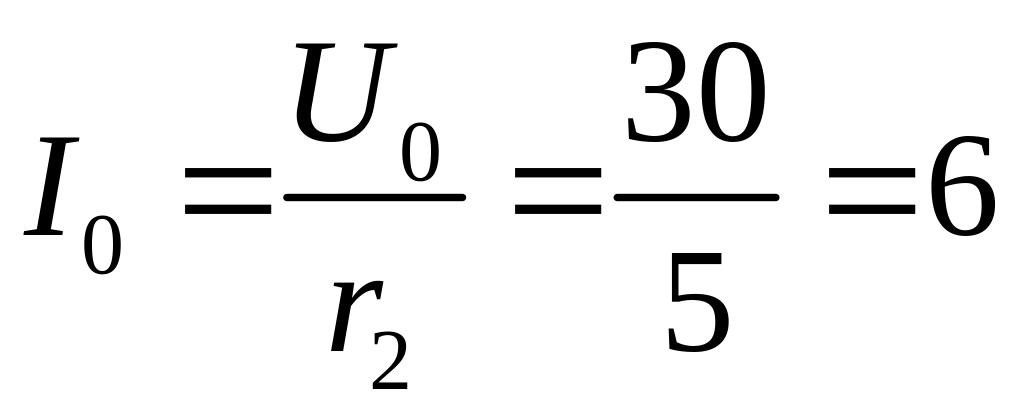 А.
А.
2) Расчёт первой гармоники.
Полное сопротивление первой гармоники:
![]() ;
;
 ;
;
![]() Ом;
Ом;
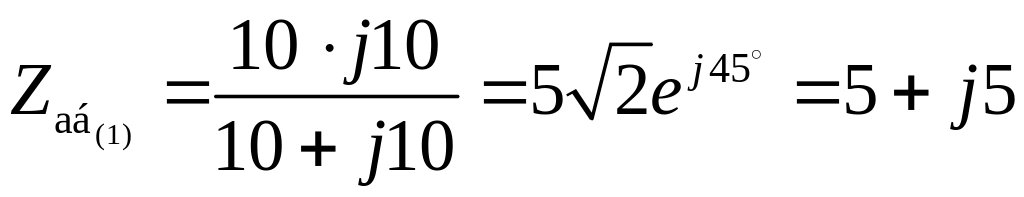 Ом;
Ом;
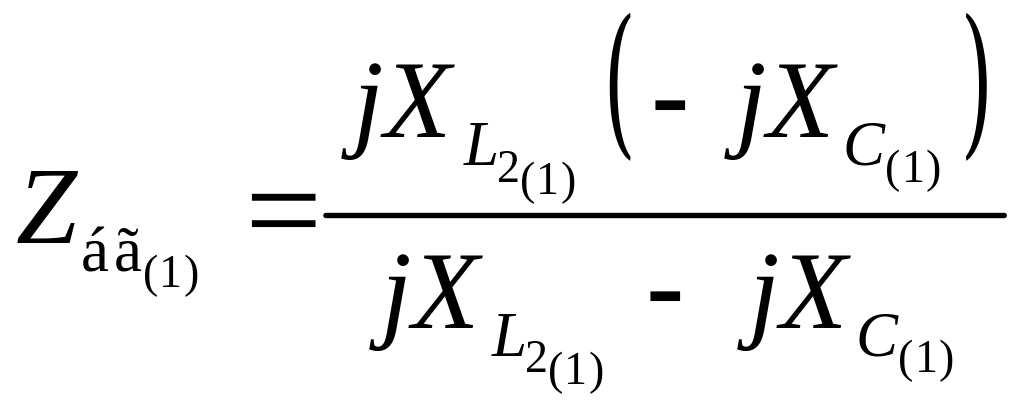 ;
;
![]() Ом;
Ом;
![]() Ом;
Ом;
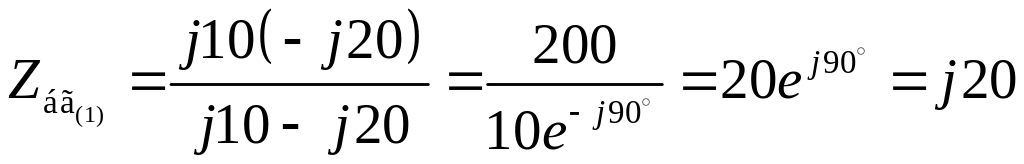 Ом;
Ом;
![]() Ом;
Ом;
 А;
А;
![]() А.
А.
Комплексные значения первой гармоники тока в сопротивлении и ёмкости C определим по правилу плеч:
 А;
А;
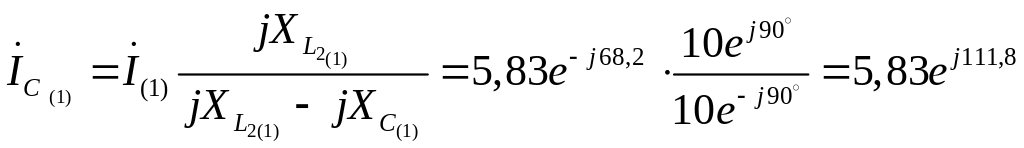 А.
А.
Действующие значения этих токов:
![]() А;
А;
![]() А.
А.
3)Расчёт пятой гармоники:
![]() Ом;
Ом;
![]() Ом;
Ом;
 Ом;
Ом;
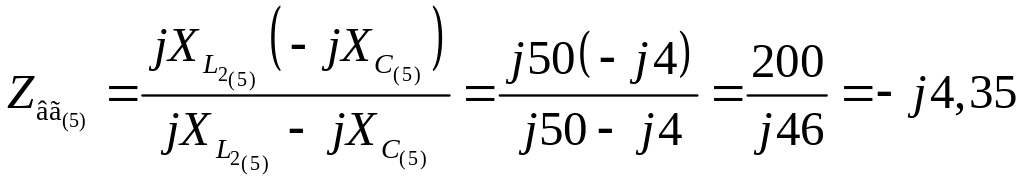 Ом;
Ом;
![]() Ом;
Ом;
 А;
А;
![]() (А);
(А);
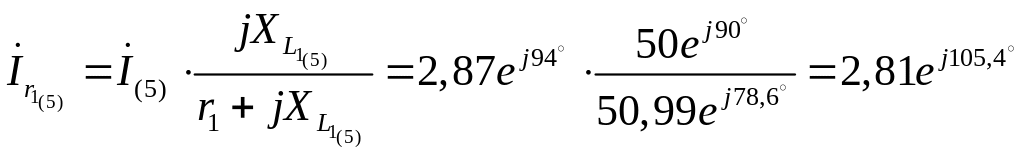 А;
А;
 А;
А;
![]() А;
А;
![]() А.
А.
Таким
образом, мы определили действующие
значения первой и пятой гармоник тока
в ветвях, где включены амперметры. Теперь
определим их показания. Амперметры в
ветвях с сопротивлением и емкостью
![]() показывают действующее значение
несинусоидального тока:
показывают действующее значение
несинусоидального тока:
![]() А;
А;
![]() А.
А.
Показание амперметра, измеряющего ток в общей ветви:
![]() (А).
(А).
Активные и реактивные мощности цепи:
![]() Вт;
Вт;
![]() ВА.
ВА.
Здесь
![]() Вт;
Вт;
![]() ВАр.
ВАр.
![]() ВА.
ВА.
Здесь
![]() [Вт];
[Вт];
![]() ВАр.
ВАр.
![]() Вт
;
Вт
;
![]() ВАр.
ВАр.
Модуль полной мощность цепи:
![]() ВА,
ВА,
где
 В
– действующее значение несинусоидального
напряжения, приложенного к цепи;
В
– действующее значение несинусоидального
напряжения, приложенного к цепи;
I
– действующее значение несинусоидального
тока (![]() ).
).
Ответ:
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Пример 9.2
|
Дано:
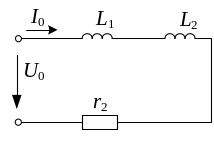
Определить действующие значения всех токов и записать законы их изменения для схемы рис. 9.7.
|
Рис. 9.7 |
Решение
1) Расчёт постоянной составляющей.
Схема рис. 9.7 для протекания постоянного тока имеет следующий вид:
|
![]() ;
;
![]() .
.
2) Расчёт для первой гармоники:
Т.к.
сопротивления параллельных ветвей
![]() и
и
![]() равны, то цепь находится в режиме
резонанса токов. Эквивалентное
сопротивление параллельного контура
равно бесконечности.
равны, то цепь находится в режиме
резонанса токов. Эквивалентное
сопротивление параллельного контура
равно бесконечности.
Схема рис. 9.7 для первых гармоник токов имеет вид:
|
Ток первой гармоники в общей ветви равен нулю, следовательно равно нулю и падение напряжения на резисторе r. Параллельный участок L-C оказывается под воздействием первой гармоники Э.Д.С., в ней замыкается ток первой гармоники (рис. 9.8).
|
Рис. 9.8 |
 ;
;
![]() ;
;
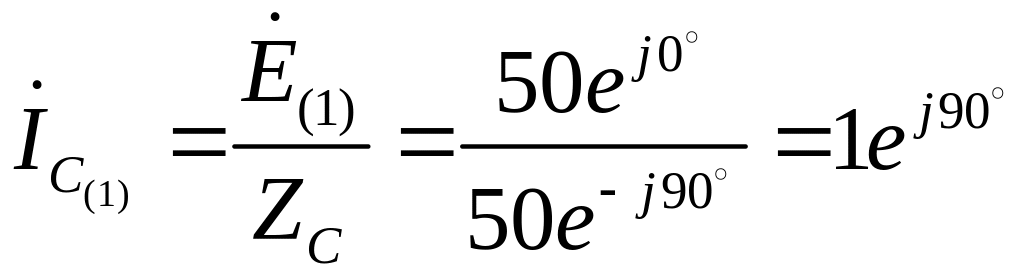 ;
;
![]() .
.
Законы изменения токов:
![]() ;
;
![]() ;
;
![]() .
.
Действующие значения токов:
![]() А;
А;
![]() А.
А.
Ответ: , , ,
![]() ,
,
![]() .
.