Лабораторная работа №3 по фтт. Край полосы собственного поглощения в кристаллах с прямой и непрямой структурами энергетических зон.

3. 1. Цели и задачи работы.

• овладение методами и приемами измерения и обработки спектров поглощения кристаллов в видимой и ближней инфракрасной области спектра;

• измерение спектров поглощения кристаллов с прямой и непря­мой структурами энергетичеких зон в области края собственного поглощения и определение по оптическим спектрам ширины запрещен­ной зоны кристаллов.

3. 2. Основные теоретические положения.

Собственное (фундаментальное) поглощение имеет место в облас­ти энергий фотонов, больших в сравнении с шириной запрещенной зоны.

Рис. 1

На зонной диаграмме (рис. 1) атому погло­щению соответствуют переходы из состояний валентной зоны в состояние зоны проводимости.

В результате поглощения квант света уничтожается, а его энергия преобразуется в энергию электронно-дырочной пары, изоб­раженной на рис. 1 светлыми и темными кружками. Таким образом, энер­гии кванта света в междузонных переходах (рис. 1) расходуется на разрыв собственных валентных связей в веществе. В результате с атомом вещества остается связанной дырка (дырка в валентной зоне), а в зоне проводимости образуется свободный электрон. Для разрыва собственных валентных связей требуется энергия квантов, большая или равная ширине запрещенной зоны (ћω E_g). Кванты света с энергией ћω< E_g не способны осуществить разрыв валентных связей в веществе и вызвать междузонные пере­ходы. Таким образом, кванты ћω<E_g не взаимодействуют с веществом, распространяясь свободно в однородной среде. Для таких квантов ћω < E_g среда является прозрачной . Энер­гии фотонов ћω = E_g определяют положение так называемого края собственного поглощения. Край собственного поглощения разгра­ничивает область «прозрачности» и «непрозрачности» кристалла, так как в области края поглощения возрастает очень быстро.

На диаграммах зависимости E(k) междузонным переходам отвечают две принципиально различные ситуации (рис. 1, б и в).

В первой из этих ситуаций (рис. 1, б) пульсы электрона и дырки в электронно-дырочной паре одинаковы k_n = k_p, так что междузонный переход на диаграмме E(k) изображается вертикальной стрелкой и называется прямым переходом.

Для второй из этих ситуаций (рис. 1, в) характерно различное значение импульсов электрона и дырки в конечном и начальном состоя­ниях, так что при междузонных переходах одновременно с изменением энергии на величину ∆k = k_n-k_p у электрона и дырки происходит изме­нение импульса на величину

Такие переходы на диаграмме зависимости E(k) изображаются наклонными стрелками и называются непрямыми переходами.

Существенное различие между прямыми и непрямыми переходами возникает из-за того, что импульс фотона намного меньше, чем возможное изменение импульса электрона и дырки в конечном и начальном состояниях, т.е. ∆k=k_n-k_p<<q, (где q - волновой вектор фотона). Поэтому с хорошим приближе­нием выполняется равенство k_n k_p , т.е. междузонные переходы с участием электрона (дырки) и фотона являются пря­мыми. Для того чтобы обеспечить значительное изменение импульса ∆k>>q помимо электрона (дырки) в переходе должно участво­вать третье тело (частица), обеспечивающая баллансирование закона сохранения импульса. Необходимое изменение ∆k дают в кристаллах фононы, так как их зона Бриллюэна совпадает с зоной Бриллюэна для электронов (см. выражение (1), лаб. работа №1). Энергия фононов обычно намного меньше, чем ширина запрещенной зоны кристалла. Поэтому участие фононов незначительно сказыва­ется на энергии участвующих в переходах фотонов.

Отметим, что величина ∆k при непрямых переходах может быть скомпенсирована не только за счет участия фононов. Необхо­димая баллансировка закона сохранения импульса может быть обеспе­чена, например, за счет нарушения периодичности кристаллического потенциала, возникающего в кристаллах за счет введения больших концентраций примеси или за счет флуктуации состава. Так как в прямых переходах участвуют две частицы, электрон и фотон, а в непрямых переходах участвуют одновременно три частицы, электрон, фотон и фонон, то вероятность прямых переходов намного выше, чем непрямых (примерно на два порядка). Поэтому в области спектра, где прямые и непрямые переходы возможны одновременно, вид оптических спектров определяется в основном прямыми пере­ходами.

Раздельно прямые или непрямые переходы проявляют себя в области края собственного поглощения. Если экстремумы энергети­ческих зон, отвечающие ширине запрещенной зоны, располагаются при одном и том же k, то край собственного поглощения определяется прямыми переходами. Если же экстремумы зон приходятся на различные точки К-пространства, то в таком полупровод­нике положение края собственного поглощения будет определяться непрямыми переходами. В случае прямых переходов положение края собственного поглощения определяется условием E_g =ћω, в то время как в случае непрямых переходов это положение опре­деляется условием ћω=E_gћω_q в зависимости от того, происходит поглощение или испускание фонона.

Рассмотрим спектральную зависимость коэффициента поглощения (ћ) в области пороговых энергий фотонов (форму края собствен­ного

поглощения). Коэффициент поглощения для междузонных пере­ходов между начальным состоянием E_i=E_v(k_i) и конечным состоянием E_f=E_g+E_c(k_f) пропорционален вероятности перехода i→f, а также числу пар энергетических уровней в валентной зоне (заполненных) и в зоне проводимости (свободных), разделенных энергией кванта света ћ. Число таких пар уровней, приходящихся на единичный интервал энергии и единицу объема вещества V=1, называется функцией комбинированной междузонной плотности состояний

N(E) = dZ/dE, (1)

где dZ - число пар уровней, разделенных энергией E в малом интервале энергий dE.

Коэффициент междузонного поглощения света может быть представлен как

α(ћω) = A·W_if·N(ћω), (2)

где А – постоянная, W_if - вероятность оптических перехо­дов от i→f.

Рассмотрим прямые междузонные переходы, изображенные на диаграмме рис. 1, б. Рассматриваемые зоны будем считать параболическими, т.е.

E_f =E_g+ћ²k_f²/2m_n^*

E_i=-ћ²k_i²/2m_p^*, (3)

а экстремумы зон находятся в центре зоны Бриллюэна.

Если нас интересует поглощение в области энергий фотонов, незначительно, превышающее ширину запрещенной зоны ћE_g, которое обусловлено переходами в малой окрестности точки K=0, то в этой окрестности вероятность прямых переходов W_if можно разложить в ряд Тейлора.

Рис. 2.

Пусть при К=0 переходы разрешены квантомеханическими правилами отбора. Тогда в разло­жении W_if по степеням К можно ограничиться первым членом, который представляет собой константу. Отметим здесь, что возмож­на ситуация, когда оптические переходы запрещены квантомеханическими правилами отбора при К=0. Для переходов, запрещенных в точке К=0, соответствующая константа в разложении равна нулю, и для описания W_if в малой окрестности точки К=0 должен быть взят следующий член разложения, который дает квадратичную зависимость W_if~k². С учетом ограничительной энергии ћω=E_g эту линейную зависимость мы можем запи­сать в виде W_if(ћω-E_g). Таким образом,

W_if const - для разрешенных переходов

W_if(ћω-E_g) - для запрещенных переходов.

Для нахождении величины N(ћω) выделим в К-прост­ранстве шаровой пояс, ограниченный двумя близкими изоэнергетическими поверхностями Е=const1 и Е+dE=const2 параболических зон, соответствующие поверхности представляют собой сферы радиусом К и К+dK. Сечение этого шарового пояса плоскостью k_z=0 представлено на рис. 8.

Объем шарового пояса (рис. 2) составляет

ΔV(k) = 4 k² dk. (4)

В соответствии с выражениями (2) (см. лаб. работу №1) на одно состояние в К-пространстве приходится объем (n1=n2=n3=1)

dV^(k)=Δk_xΔk_yΔk_z=(2π/aN_x)(2π/aN_y)(2π/aN_z)=8π³/a³*N_xN_yN_Z=8π³/V, (5)

где V - объем кристалла.

Тогда из (4) и (5) найдем число состояний, заключенных в интервале энергий dE от Е до Е+dE для кристалла единичного объема V=1

ΔV^(k)/dV^(k)=k²dk/2π². (6)

С учетом того, что в каждом состоянии (ячейке К-пространст­ва) может находится два электрона, полное число уровней представим как

dZ=2ΔV^(k)/dV^(k)=k²dk/π². (7)

Выразим в (7) k² и dk через энергию квантов света, участ­вующих в переходе. Для этого воспользуемся законом сохранения энергии

ћω=E_f–E_i, (8)

который с учетом (3) позволяет найти

ћω–E_g=ћ² k²(1/m_n^*+1/m_p^* )/2=ћ² k²/2m_r^*, (9)

где m_r^*=m_n^*m_p^*/(m_n^*+m_p^*) - приведенная эффективная масса электронно-дырочной пары.

Из (7) и (9) получим

N(ћω)=dz/d(ћω)= ((2m_r^* )^3/2/2π² ћ³)/(ћω–E_g )^1/2. (10)

и из выражений (2) и (10) найдем коэффициент поглощения для прямых разрешенных переходов при К=0

α(ћω) = A^* (ћω – E_g)^1/2, (11)

где А^* - новая константа, объединяющая величины А, W_if и постоянный коэффициент в выражении (11). Было показано, что для этой константы в явном виде справедливо

A^*=e²(2m_n^*m_p^*/(m_n^*+m_p^*))/(nchm_n^*), (12)

где е - заряд электрона, n - показатель преломления среды, с - скорость света, h - постоянная Планка.

Как видно, в области края собственного поглощения, коэффициент поглощения, определяемый прямыми разрешенными переходами возростает в зависимости от энергии фотонов по корневому закону.

Спектральная зависимость α(ћω) в области края собствен­ного поглощения может быть использована для определения ширины запрещенной зоны кристалла. Для этого необходимо построить зависимость α²(ћω) от энергии фотонов и произвести экстраполяцию полученной линейной зависимости в область ћω=0. Точка пересечения графика с осью абсцисс и даст энергию ћω=E_g.

Для непрямых переходов абсолютный максимум валентной зоны и минимум зоны проводимости приходится на различные точки К-пространства, так что наименьший энергетический зазор между валентной зоной и зоной проводимости (ширина запрещенной зоны) ограничен здесь непрямыми переходами (рис. 1, в).

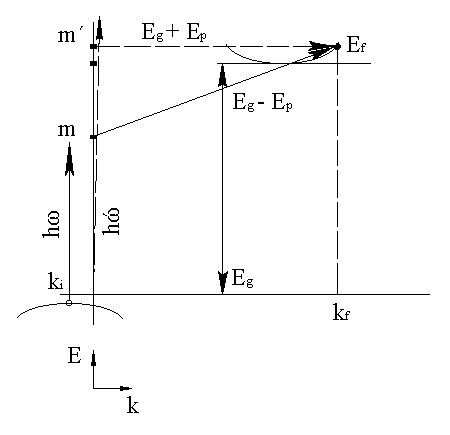
Рис. 3.

Законы сохранения энергии и импульса для непрямых переходов могут быть записаны как

E_f–E_i=ћωE_p (13)

K_p-k_i=Δk=q_p, (14)

где Е_p и q_p - энергия и волновой вектор фонона; знак (+) соответствует поглощению фонона, а знак (-) - испусканию фонона. На рис. 1, в непрямой переход из начального состояния i в конечное f изображается наклонной стрелкой. Этот переход из начального состояния k_i в конечное k_f с участием фотона и фонона представим в два этапа, как это изображено на рис. 3.

На первом этапе электрон в состоянии k_i поглощает фотон с энергией ħω и совершает вертикальный переход в промежуточное состояние m, находящееся в пределах запрещенной зоны. При переходе в промежуточное состояние m волновой вектор сохраняется. Состояние m в пределах запре­щенной зоны называется виртуальным. Пребывание в этом состоянии разрешено вследствие принципа неопределенности Eτ≤ħ, где Е - энергия состояния, а τ – время жизни этого состояния. Для рассматриваемых нами междузонных переходов E≈E_g≈1Эв и тогда τ=ħ/Eg≈10^-15 c т.е. время жизни виртуального состояния очень мало. Однако, за это время должен быть инициирован второй этап перехода, состоящий в том, что электрон, находящийся в состоянии m, поглощает фонон. В результате поглощения фонона электрон дополнительно увеличивает свою энергию так, что ħω+E_p=E_f-E_i (выражение (13)), а также изменяет свой волновой вектор на величину q_f=k_f-k_i (выражение (14)) и оказывается в конечном состоянии E_f=E_c(k_f).

Аналогичным образом может быть представлен непрямой переход из состояния E_i в состояние E_f и испусканием фонона через промежуточное (виртуальное) состояние запрещенной зоны m′, где

ħω-E_p=E_f-E_i и –q_p=k_f-k_i (выражения (13) и (14)).

При вычислении функции комбинированной плотности состояний при непрямых переходах необходимо учесть все пары состояний вблизи EiиE_f, разделенные энергией ħω±E_pфунк­ция плотности состояний вблизи начальных состояний в валентной зоне имеет вид

N(E_i)=1/(2∏²ħ³)(2m_p^*)^3/2E_i^1/2, (15)

Аналогично для конечных состояний в зоне проводимости

N(E_f)=1/(2∏²ħ³)(2m_n^*)^3/2E_f^1/2, (16)

или с учетом закона сохранения энергии (выражение (12))

N(E_g)=1/(2∏²ħ³)(2m_n*)^3/2(ħω-E_g±E_p+E_i)^1/2. (17)

Комбинированная плотность состояний опрееделяется тогда интегрированием по изоанергетической поверхности ħω=E_f-E_i от произведения плотности состояний в зонах, т.е. N(E_i)N(E_f). Таким образом, (рис. 3)

(ħω-E_g±E_p)

N~∫E_i^1/2(ħω-E_g±E_p+E_i)^1/2dE_i=[ħω-(E_g±E_p)]², (18)

0

где знак (+) соответствует испусканию фонона, а знак ( - ) - поглощению фонона.

Кроме того, коэффициент поглощения с участием фононов будет зависеть от числа фононов, возбуждаемых в кристалле при данной температуре. Вероятность поглощения фонона при непрямых переходах будет тем большей, чем число фононов, определяемое статистикой Бозе-Эйнштейна.

f_p=1/(e^Ep/(kT) -1), (19)

а коэффициент поглощения света для непрямых переходов с погло­щением фононов пропорционален числу фононов, т. е. α_A~f_p.

Для переходов с испусканием фононов вероятность процесса пропорциональна увеличению числа фононов на один, т. е. функции

f_p+1=1/(1-e^-Ep/(kT)) (20)

и коэффициент поглощения и испускания фононов α_E~(f_p+1).

Тогда, объединия (17) (18)и(20),результирующий коэффициент поглощения света для непрямых переходов, разрешенных при ħω=E_g, можем представить в виде

α(ħω)=α_A+α_E=C₁[ħω-(E_g-E_p)]²/(e^Ep/(kT)-1)+ C₂[ħω-(E_g+E_p)]²/(1-e^-Ep/(kT)) (21),

где α_A и α_E - компоненты коэффициентов поглощения с поглощением и испусканием фононов, C₁ и C₂ - постоянные множители. Теперь, в случае непрямых переходов спектральная зависимость α(ħω) имеет два порога: E_g-E_p для составляющей α_A с поглощением фонона и E_g+E_p для составляющей α_E

Рис. 4.

с испусканием фонона. Спектральные зави­симости величины (α(ħω))^1/2 для непрямых разрешенных переходов будут линейны в зависимости от энергии квантов света, как это показано на рис. 10.

α=-1/d^*ln(T/(1-R)²)

Как видно, экстраполяция величин α_E^1/2 и α_A^1/2 к нулевым значениям позволяет определить величины (E_g±E_p) и найти таким образом ширину запрещенной зоны и энергию фонона, участвующего в переходе.