Виды вращательного движения твердого тела в зависимости от ускорения:

1) равномерное вращение — это движение тела с постоянной угловой скоростью:

ω = φ / t = const,

φ = ω t,

ε = 0.

Линейные скорости и ускорения точек : , ;

2) равнопеременное — это движение с постоянным уг­ловым ускорением:

ε=(ω-ω₀)⁄t=const;

φ = ω₀ t + ε t²⁄ 2;

ω = ω₀ + ε t.

Линейные скорости и ускорения точек:

Тема 1.10 Сложное движение точки

В некоторых случаях движущиеся тела, которые принимаются за матери­альные точки, могут совершать сложное движение (например, движение человека в вагоне движущегося поезда).

Сложное движение точки— это движение точек, рассматриваемое одновременно по отношению к двум системам отсчёта, одна из которых считается неподвижной, а вторая определённым образом движется по отношению к первой

В сложном движении различают три движения: абсолютное, переносное и относительное.

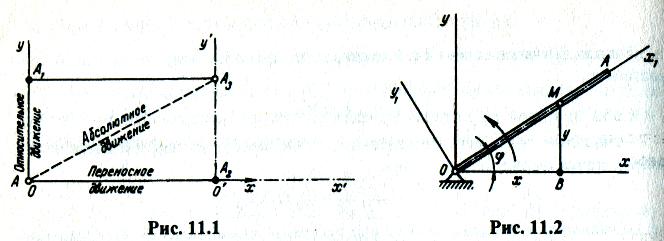Абсолютное движение — это движение точки относительно неподвиж­ной системы координат. (Движение человека по палубе корабля по отношению к берегу)

Абсолютное движение точки складывается из переносного движения, т.е. дви­жения подвижной системы координат относительно неподвижной (движение корабля по отношению к берегу), и относительного движения, т.е. движения точки относительно подвижной системы координат (движение человека относительно палубы корабля).

Скорость сложного движения называется абсолютной скоростью.

Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:

абс = пер + отн - теорема сложения скоростей.

Тема 1.11 Сложное движение твердого тела (Плоскопараллельное движение)

Плоскопараллельным движением называется такое движение, при котором все точки тела перемещаются в плоскостях параллельно какой-то одной плос­кости, называемой основной. Пример такого движения: движение колеса автомобиля на прямом участке пути, движение шатуна кривошипно-шатунного механизма.

Плоскопараллельное движение изучается двумя методами:

1. методом разложения плоскопараллельного движения на поступатель­ное и вращательное;

2. методом мгновенных центров скоростей.

В основе первого метода лежит теорема: всякое плоскопараллельное движение может быть получено с помощью поступательного и вращательного движений, которые происходят одновременно (рис. 1.48).

Поступательное движение тела можно считать переносным, а вращатель­ное — относительным. Тогда вектор абсолютной скорости какой-то точки А будет равен скорости поступательного движения какой-то другой точки О плюс скорость вращательного движения точки А относительно точки О (см. рис. 1.48):

, .

Точка, вокруг которой происходит относительное вращательное движе­ние, называется полюсом вращения.

Точка О - полюс вращения.

Таким образом, скорость любой точки тела при плоскопараллельном дви­жении в данный момент времени равна сумме скорости полюса вращения и вращательной скорости данной точки относительно полюса:

_В= _о + _Во.

В основе второго метода лежит понятие мгновенного центра скорос­тей (МЦС).

Мгновенный центр скоростей — это точка плоской фигуры, скорость ко­торой в данный момент времени равна нулю.

Всегда можно на фигуре найти такую точку. Например, возьмем скорость какой-то точки А, которую примем за полюс вращения. Отложим отрезок АР, перпендикулярный v_А, где , тогда скорость точки Р равна , причем (рис. 1.49).

Таким образом, Vр=V_А-V_А = 0.

Мгновенный центр скоростей всегда лежит на пря­мой, проведенной из какой-либо точки фигуры пер­пендикулярно направлению скорости этой точки.

Скорость любой точки фигуры прямо пропорцио­нальна ее расстоянию до МЦС:

Рис 1.49

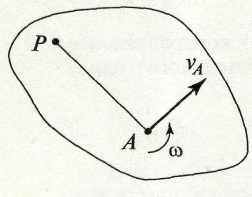
Способы нахождения МЦС:

1. Известны угловая скорость ω и скорость какой-то точки v_A.

МЦС точки Р - на перпен­дикуляре, восстановленном из точки А к вектору ско­рости на расстоянии (см. рис. 1.49):

2. Известны направления скоростей двух точек v_A и v_B.

МЦС - на пересечении перпендикуляров, восстанов­ленных из точек А и В к направлениям их скоростей (рис. 1.50).

3. Известно, что векторы скорости двух точек и параллельны друг дру­гу, направлены в одну сторону перпендикулярно отрезку АВ и не равны по величине.

МЦС - в точке пересечения прямой, соединяющей начала векторов и , с прямой, соединяющей их концы (рис. 1.51).

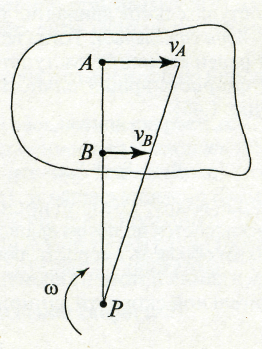
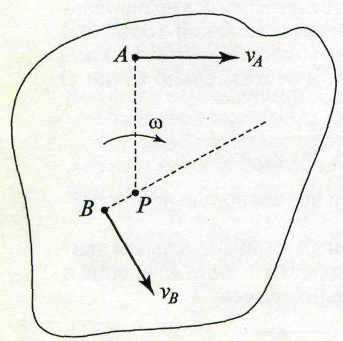
Рис. 1.50 Рис 1.51

4. Известно, что векторы скорости двух точек и параллельны друг другу, но направлены в противоположные стороны.

МЦС - на пересечении прямых, соединяющих начала и концы векторов скорости (рис. 1.52).

5. Известно, что плоская фигура без скольжения катится по неподвижной прямой.

МЦС - находится в точке соприкосновения фигуры с пря­мой (рис. 1.53).

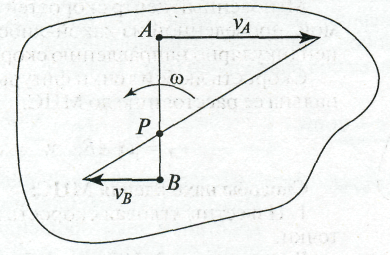
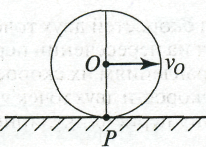
Рис.1.52 Рис 1.53