3.4.3. Последовательностные детерминированные модели

В отличие от комбинационных моделей при составлении последовательностных моделей необходимо отражать однозначное соответ­ствие состояний выходов комбинациям состояний входов как в дан­ном такте, так и в предыдущих. Следовательно, одна и та же комбина­ция входов в данном такте может вызвать переход в разные новые со­стояния в зависимости от того, каким было предшествующее состояние. Поэтому в модели должны быть отражены не только данный такт, но и предыстория.

В зависимости от сложности объекта используются различные виды моделей. В простейшем случае применяются циклограммы, в которых состояния отражают условным изображением включенного или от­ключенного исполнительного элемента в виде наличия или отсутст­вия линии. При большом числе состояний применяются таблицы со­стояний и графы. Более конкретно методика составления моделей изложена на примерах.

Циклограмма. Она представляет собой ряд горизонтальных строк, равных числу командных и исполнительных элементов. Строки услов­но разбиты на отрезки, число которых равно числу элементарных техно­логических тактов. Включенное состояние элемента на строке обозна­чается сплошной линией, отключенное — отсутствием ее. Вертикальными линиями на циклограммах по­казана "передача управления" -причинно-следственные связи меж­ду командными и исполнительны­ми элементами.

Когда элемент включен, совокупность тактов называется периодом включения, а когда отключен - периодом отключения. Такт, предшест­вующий периоду включения, называется включающим, а периоду от­ключения — отключающим.

Пример 3.8. Рассмотрим циклограмму работы грузового подъемни­ка (рис. 3.8). Грузовой подъемник с тележкой от подачи кратковре­менной команды кнопкой SB (пуск) идет вверх [кнопка SB включа­ет контактор "Вперед" КМ1 (SB -> КМ1), после чего отключается (такт 1)1. В начале движения отключается нижний конечный выклю­чатель SQ2 (такт 2). После достижения крайнего верхнего положе­ния кабина воздействует на верхний конечный выключатель SQ1, кото­рый дает команду на отключение КМ1 (такт 3,SQ1 -+КМ1). Контак­тор КМ1 отключается (такт 4). После выката тележки отключается ко­нечный выключатель SQ3 (такт 5) и включается контактор "Назад" КМ2, подъемник идет вниз (такт 6, SQ3 -»■ КМ2), отключается SQ1 (такт 7). После воздействия внизу на нижний конечный выключатель SQ2 отключается КМ2 (такт 8, SQ2 -> КМ2), кабина останавливается (такт 9).

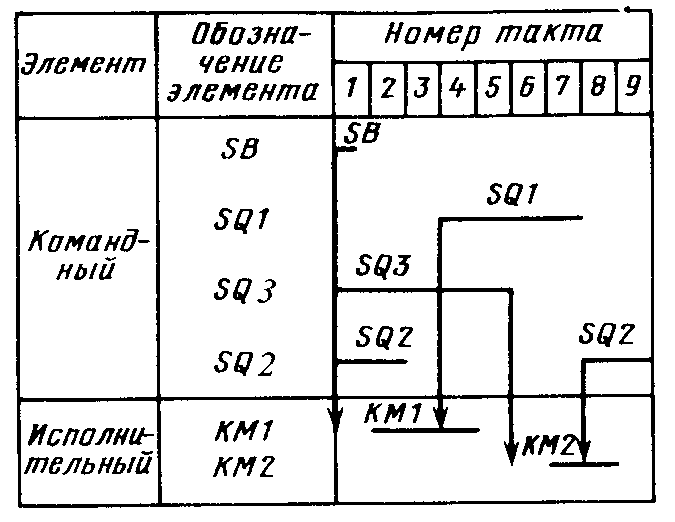
Рис. 3.8. Циклограмма работы грузо­вого подъемника

4.3.1. Элементы теории дискретных автоматизированных устройств

Под дискретным автоматизированным устройством понимают уп­равляющее устройство, осуществляющее переработку априорной и текущей информации в управляющую, причем носителями всех пере­численных составляющих информации являются дискретные по уров­ню и во времени сигналы. Это означает, что состояние сигнала каж­дого входа (выхода) автоматизированного устройства характеризует­ся двумя уровнями: минимальным, условно обозначаемым 0, и макси­мальным, обозначаемым I. При наличии нескольких входов (выходов) комбинацию минимальных и максимальных (нулевых и единичных) уровней можно воспринимать двояко:

как наличие или отсутствие на каждом входе (выходе) задающего или командного сигнала, поступающего на какой-либо исполнитель­ный элемент;

как кодовую комбинацию, обозначающую, например, двоичное число, количество разрядов п которого равно количеству входов (вы­ходов). Следовательно, можно говорить о многоуровневом выходном сигнале с числом уровней N=2".

В первом случае дискретное логическое автоматизированное уст­ройство решает задачи логического анализа ситуации, определяемой рядом действующих или отсутствующих факторов, во втором — ариф­метическое устройство, осуществляет преобразование информации пу­тем выполнения арифметических операций над числами.

Как логические, так и арифметические устройства реализуются при­менением ограниченного числа типовых элементарных операций над дискретными сигналами и сходных методов синтеза и анализа.

Дискретизация по времени означает, что в течение конечного ин­тервала времени f_;-, именуемого тактом, состояние сигнала либо их комбинация остаются неизменными. Пронумерованная последователь­ность таких тактов образует автоматное время.

Дискретные управляющие устройства в соответствии с требования­ми технологического цикла (см. § 2.3) бывают комбинационными и последовательностными. Первые характерны тем, что комбинация состояний выходных сигналов У_кг- в данном такте t_i однозначно оп­ределяется комбинацией входных сигналов X, в этом же такте време­ни, т.е.

где X — оператор (алгоритм) преобразования.

Комбинационные автоматы называют также автоматами с нулевой памятью.

У последовательностных автоматов комбинация состояний выхо­дов в такте tj зависит не только от комбинации состояний входов в данном такте, но и от того, какими были комбинации состояний вхо­дов в п предыдущих тактах, т.е.

Их называют также автоматами с ненулевой памятью, так как для вы­работки своих выходных (управляющих) сигналов они должны не только "знать", что сейчас (в данном такте) происходит на входе, но и "помнить", что было раньше.

Переключательной функцией (ПФ) называют переменную, значе­ния которой зависят от значений других двоичных переменных—аргу­ментов. Переключательная функция задается в виде соответствия ее значения каждому набору (комбинации) значений ее аргументов. Пе­реключательные функции считаются разными, если отличаются значе­ниями хотя бы для одного набора.

При п аргументах число наборов N = 2", а число переключательных функций

М = 2^N = 2²".

По характеру реакции на входное воздействие различают асинхрон­ные автоматы, у которых изменение состояния выходов происходит сразу после изменения входных, и синхронные, у которых изменение выходов происходит лишь в том случае, если после изменения вход­ных сигналов поступит синхронизирующий сигнал, разрешающий пре­образование.

Для создания самого сложного дискретного автомата любого типа достаточно иметь элементы, реализующие операцию ИЛИ—НЕ (инвер­сия дизъюнкциии или операция Пирса) либо операцию И—НЕ (инвер­сия конъюнкции или операция Шеффера), т.е. так называемый функ­ционально полный набор.

Последовательностные автоматы отличаются от комбинационных также наличием обратных связей, по которым на входы автомата пода­ются сигналы, соответствующие состоянию выходов в предыдущем такте.

Ниже рассмотрены достаточно обобщенные методы анализа и синте­за дискретных автоматов с использованием элементов минимальной и средней степеней интеграции.

Основные этапы синтеза дискретного автомата следующие:

1) составление задания на разработку в виде содержательного опи­сания, где формулируются требования управляемого объекта к авто­мату, т.е. описания, на какой исполнительный элемент объекта и в каком такте должен быть подан минимальный (0) или максималь­ный (1) уровень сигнала данного выхода автомата, чтобы с учетом состояния задающих входов и выходов, воспринимающих сигналы обратных связей, обеспечить требуемое функционирование управ­ляемого объекта;

2) получение формальной модели автомата на основе содержатель­ного описания в виде таблиц, графов, матриц и т.п. (см. § 3.4) ;

3) получение на основе модели объекта исходной или минималь­ной формы аналитического представления оператора преобразования, реализуемого автоматом и обеспечивающего требуемый закон функцио­нирования управляемого объекта. Эта часть синтеза является основной и базируется на аксиомах и постулатах Булевой (двоичной) ал­гебры;

4) разработка принципиальной схемы автомата на основе получен­ной в п. 3 его формальной модели и используемой конкретной элемент­ной базы;

5) разработка и согласование узлов связи автомата с оператором и управляемым объектом, защита от помех и т.п.

РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИИ

Каждое устройство, состоящее из соединенных меж­ду собой катушек реле и контактов¹ (контактов реле, кнопок, датчиков), можно описать с помощью булевых функций² и, наоборот, любую логическую функцию можно реализовать с помощью схемы, состоящей из соединенных между собой катушек и контактов реле. Обычно при записи функций катушки реле обозначают­ся большими буквами, а контакты — маленькими. Вклю­ченное состояние реле (контакта реле) записывается как Р=1 (р=1), отключенное состояние реле (контакта реле)—Р=0 (р=0). Для простейшей схемы, изобра­женной на рис. 2-3,а, можно записать:

Р=1, если а=\, и Р=0, если а=0, или Р—а.

В схеме рис. 2-3,6 реле Р включено, когда отключе­но реле А, или

Р=а.

На схеме рис. 2-3,0 реле Р включено, если включены оба реле А и В:

P=ab,

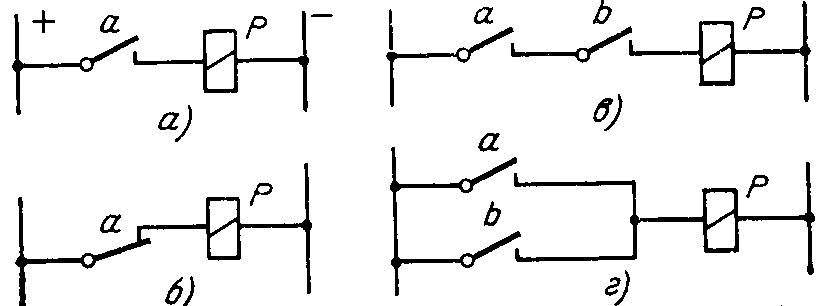
Рис. 2-3. Реализация основных логических функций.

а на схеме 2-3,г реле Р включено, если включено хотя бы одно реле А или В:

Р = а\/Ь.

Отсюда вытекают общие правила: последовательно­му соединению контактов соответствует конъюнкция, параллельному — дизъюнкция, а нормально замкнутый контакт в схеме соответствует отрицанию Следуя этим правилам, легко выразить функцию, реализованную схемой на рис. 2-4,а:

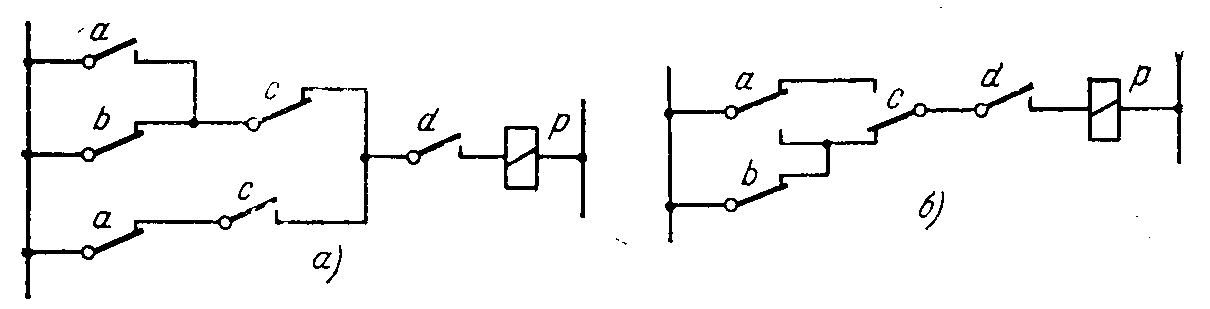
Рис. 2-4. Схемы, реализующие функцию

Построение контактной схемы, соответствующей ана­литическому выражению логической функции, также не представляет трудности.

В целях уменьшения числа контактных пружин мож­но соединять контакты одного и того же реле, имеющие общую точку: замыкающий и размыкающий контакты заменить одним переключающим (рис. 2-4,6).