3.4 Вывод

Научились строить графики без использования компонентов TChart. Анализируя результат показывает что графики построенные с помощью TChart и Tcanvas совпадают.

Задание 4

Интерполяция данных

4.1 Постановка задачи

По заданным узловым точкам построить интерполяционную кривую. Количество узлов интерполяции 5, количество узлов между точками 10.

4.2 Краткие теоретические сведения

Интерполяция подразумевает «соединение» точек выборки данных кривой той или иной степени гладкости.

По определению интерполяция означает построение функции f(x), аппроксимирующей зависимости y(x) в промежуточных точках (xi). В точках

(xi) значение интерполяции функции полностью совпадает с исходными данными f(xi)=y(xi).

Различают два вида интерполяции:

Линейная

1. А) Кусочно-построенная. Ее смысл в том, что на каждом промежутке между экспериментальными точками f(x) представляет собой const, равную значению величины на границе.

В) Кусочно-линейчатая интерполяция, которая представляет искомую зависимость в виде ломанной линии.

Функция f(x) представляет собой кривую соединенную исходными точками: f(x)=y

2. Кубическая (сплайн) интерполяция

Сплайн - фрагмент полинома. Смысл в том, что в каждом промежутке между узловыми точками осуществляется апроссимация в виде полиниальной зависимости f(x), при этом для каждого шага соединяется свой полином, причем его коэффициент подбирается так, чтобы на границах шага выпали угловые стыковки. Наиболее часто применяют кубические сплайны, т.е. полином 3-ей степени.

4.3 Выполнение задания

Код программы линейной интерполяции:

double lininterpol(double xi,double yi,double xi1,double yi1, double x){

return ((yi*((x-xi1)/(xi-xi1)))+(yi1*((x-xi)/(xi1-xi))));

}

void __fastcall TForm1::Button1Click(TObject *Sender)

{

Series1->Clear();

Series2->Clear();

int n=5;

int m=10;

double h=0.1;

double *d=new double [n] ;

for (int i=0; i<n; i++){

d[i]=i*i/exp(i);

Series1->AddXY(i,d[i],"",clTeeColor);}

double x; double y;

for(int i=0;i<n-1;i++){

x=i;

for(int j=0;j<m;j++){

y=lininterpol(i,d[i],i+1,d[i+1],x);

Series2->AddXY(x,y,"",clTeeColor);

x+=h;

}}

delete[]d; }

Результат работы программы линейной интерполяции (см Рисунок 4.1)

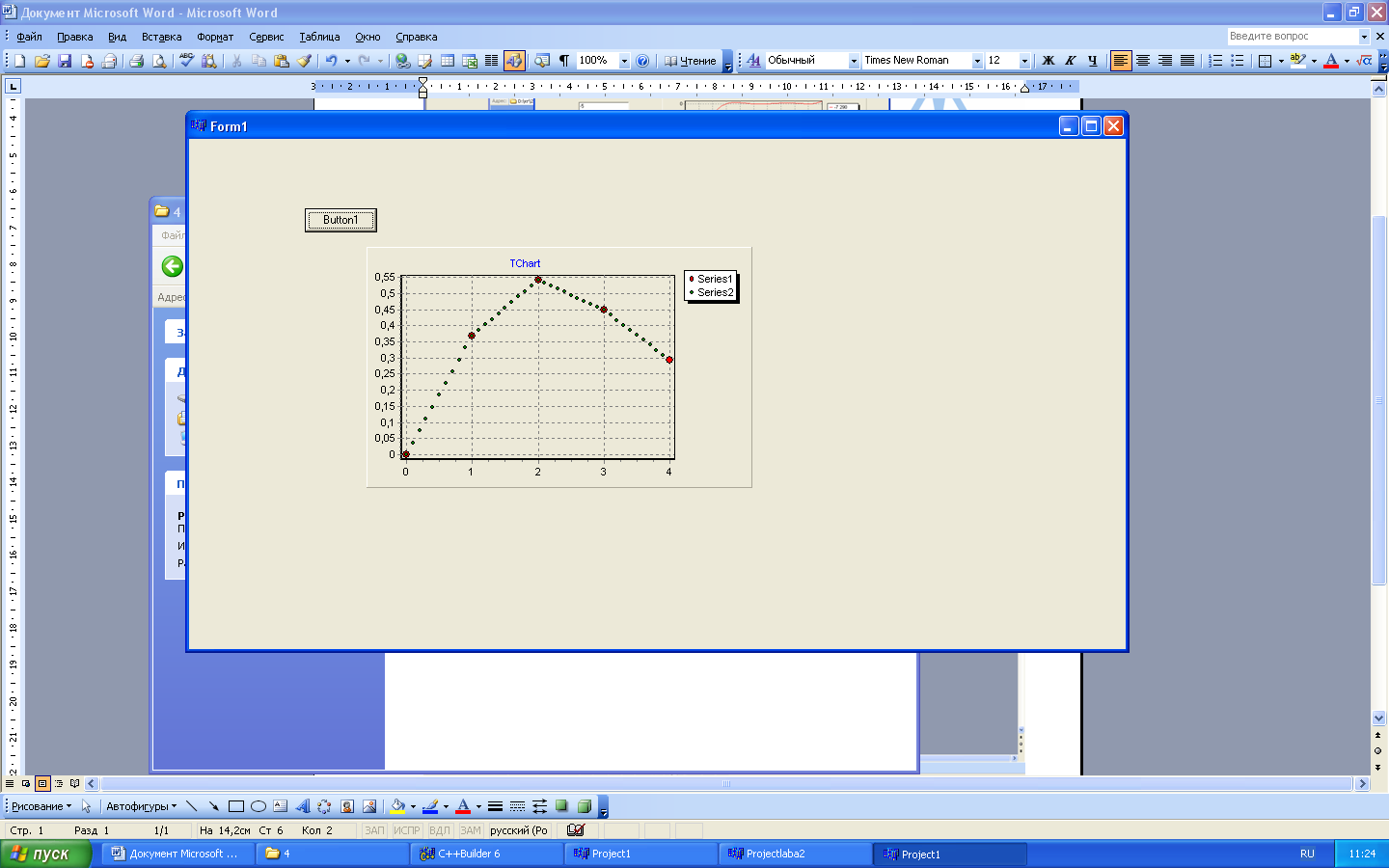
Рисунок 4.1 –Интерполяционная кривая

4.4 Вывод

Научились строить по заданным узловым точкам интерполяционную кривую.

Заключение

В ходе расчетно-графическое задание научились использовать пакет Microsoft office для оформления технической документации, работать в среде Visio, строить и создавать графики функций с использованием компонента Tchart, и класса Tcanvas в программе C++ Builder. Научились по заданным узловым точкам строить интерполяционную кривую.