Расчетно-графическая работа № 4. Сложное сопротивление Задание 4.1. Расчет валов.

Имеется ведущий вал, на который насажен шкив и косозубая шестерня (рис. 4.1). Движение на вал передается через ременную передачу от электродвигателя (на рис. не показан), затем крутящий момент посредством зубчатого зацепления передается на ведомый вал (показан пунктиром). Подшипник 4 – радиально-опорный, остальные – радиальные. Ветви ремня заменены усилиями T и t. Исходные данные отображены в табл. 4.1.

Требуется:

1. Определить диаметр вала d из условия прочности.

2. Выполнить проверочный расчет на выносливость.

Рис. 4.1 Ведущий вал

Табл. 4.1 Исходные данные к заданию 4.1

Параметр	l1	l2/l1	l3/l1	D1	D2/D1	β	φ	Опорные точки	Место шкива	Место шестерни	Марка стали	N	n	Форма концентратора	Место концентратора	d*/d	r/d	do/d	t/r	Поверхность в зоне конц.	∆Миз	∆Мкр
	м	-	-	м	-	град.	град.	-	-	-	-	кВт	об/мин	-	-	-	-	-	-	-	±%	±%
1	0,10	1,0	2,0	0,16	1,6	10	30	1;4	3	2	35	1,5	100	1	2	1,2	0,05	0,08	3,0	1	20/40	30/50
2	0,15	1,1	1,9	0,18	1,5	15	45	1;4	3	2	40	1,8	120	2	3	1,3	0,06	0,10	2,8	2	30/50	30/60
3	0,20	1,2	1,8	0,20	1,4	8	60	1;3	4	2	50	2,6	140	3	4	1,4	0,08	0,12	2,6	3	40/40	40/30
4	0,25	1,3	1,7	0,22	1,3	15	120	1;3	4	2	35Х	3,5	160	1	2	1,5	0,10	0,14	2,4	4	60/20	20/30
5	0,30	1,4	1,6	0,24	1,2	10	135	2;4	3	1	40Х	3,8	180	2	3	1,6	0,12	0,16	2,2	5	70/10	20/40
6	0,35	1,5	1,5	0,26	1,1	8	150	2;4	3	1	45Х	4,6	200	3	1	1,7	0,14	0,18	2,0	6	30/60	20/50
7	0,40	1,6	1,4	0,28	1,0	8	180	2;3	4	1	35ХН	4,8	400	1	1	1,8	0,16	0,20	1,8	7	20/70	10/70
8	0,45	1,7	1,3	0,30	0,9	15	90	2;3	4	1	40ХН	5,6	420	2	4	1,9	0,18	0,22	1,6	1	10/60	70/10
9	0,50	1,8	1,2	0,32	0,8	10	110	1;4	3	2	20Г	6,6	460	3	3	2,0	0,20	0,24	1,4	2	30/30	20/40
0	0,60	2,0	1,1	0,34	0,6	8	100	1;4	3	2	45	7,6	500	1	3	1,9	0,22	0,26	1,2	3	50/50	30/50
	а	б	в	в	б	а	а	в	в	в	б	а	а	б	в	в	б	а	а	б	в	в

Д ополнительные данные:

Поверхность в зоне концентратора

1. - Шлифованная

2. - Полированная

3. -После чистовой обработки

4. -Грубо обточенная

5. -Необработанная после прокатки

6. -Корродированная в пресной воде

7. -Корродированная в морской воде

Порядок решения:

1. Определяем крутящий момент на валу

,

где N – мощность, передаваемая валом, кВт; n – число оборотов вала, об/мин.

2. Находим суммарное усилие от натяжения ветвей ремня

,

где натяжение t определяется по выражению:

,

здесь D₂ – диаметр шкива, м.

Усилие S раскладываем на вертикальную и горизонтальную составляющие:

где φ – угол наклона ветвей ремня.

3. Определяем усилия, возникающие от зубчатого зацепления:

Окружная сила , D₁ – диаметр шестерни;

Осевая сила , β – угол наклона зубьев шестерни;

Радиальная сила , α = 20˚ – угол нарезки зуба;

Сосредоточенный момент .

4. Составляем пространственную расчетную схему вала, с действующими на него усилиями от ременной передачи, зубчатого зацепления и реакциями в опорах. Решаем задачу по принципу независимости действия сил: на изгиб в 2-х плоскостях, на кручение и растяжение (сжатие).

В расчете на изгиб статическую неопределимость раскрываем при помощи уравнения трех моментов. В вертикальной плоскости строим эпюры поперечных сил Q_y и изгибающих моментов M_z, а в горизонтальной – Q_z и M_y.

После расчета на кручение и на растяжение (сжатие) строятся эпюры продольных сил N_x, крутящих моментов M_x, и суммарных изгибающих моментов M_Σ.

Суммарный изгибающий момент в i-том сечении определяется по теореме Пифагора .

5. Выполняем расчет на прочность по третьей теории (наибольших касательных напряжений)

,

где , , , .

Откуда .

Полученный диаметр округляем до стандартного наибольшего d_ст.

6. Делаем проверочный расчет на выносливость:

,

здесь , , .

Допускаемые нормальные напряжения на выносливость определяются:

,

где ,

,

,

– действительный (эффективный) коэффициент концентрации напряжений,

α_КТ – теоретический коэффициент концентрации напряжений,

q – коэффициент чувствительности материала к концентрации напряжений,

α_М – масштабный коэффициент,

α_П – коэффициент поверхностной чувствительности,

r – коэффициент асимметрии цикла, который определяется по ΔМ_ИЗ, например, при , r = -0,5.

Допускаемые касательные напряжения на выносливость определяются аналогично:

,

где ,

,

,

r определяется по ΔМ_КР.

Если условие не выполняется, то делаем пересчет диаметра вала по следующему выражению:

.

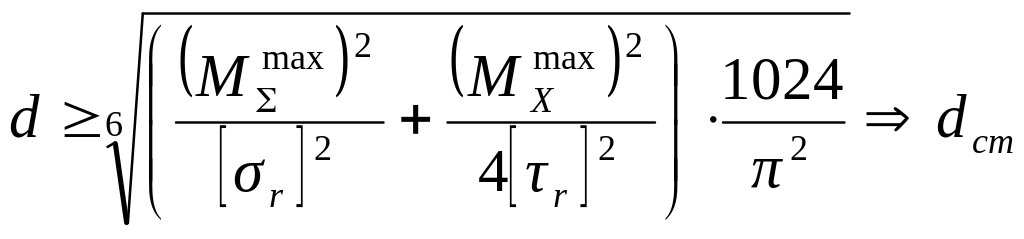На этом решение задачи заканчивается.