Задание 2.2. Изгиб рам.

Дана плоская рама, на которую действует равномерно распределенная нагрузка, сосредоточенная сила и момент (рис. 2.2). Величины нагрузок и длины участков заданы в табл. 2.2.

Требуется построить эпюры внутренних силовых факторов.

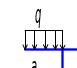
Рис. 2.2 Расчетные схемы рам

Табл. 2.2-Данные к заданию 2.2

	1	2	3	4	5	6	7	8	9	0	шифр
Схема	I	II	III	IV	V	VI	VII	VIII	IX	X	в
Р, кН	20	30	40	50	60	10	15	5	25	20	а
М, кН∙м	5	10	6	8	4	12	15	7	16	14	б
q, кН/м	10	8	9	10	12	14	15	20	22	18	в
а, м	1	0,9	0,8	0,7	2	0,5	1,5	1,6	1,8	2,5	а

Пример:

На рис. П2.2 изображена плоская рама, на которую действует равномерно распределенная нагрузка q. Длины участков равны а. Рама имеет опору в виде жесткой заделки. Необходимо построить эпюры продольных и поперечных сил, а также изгибающих моментов.

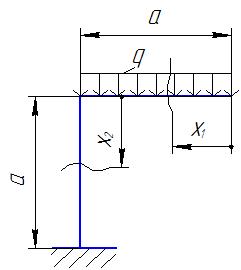
Рис. П2.2 Расчетная схема плоской рамы

Решение:

1) Определяем внутренние силовые факторы:

1-й участок (0≤х₁≤а)

;

; ; .

; ; .

2-й участок (0≤х₁≤а)

; ; .

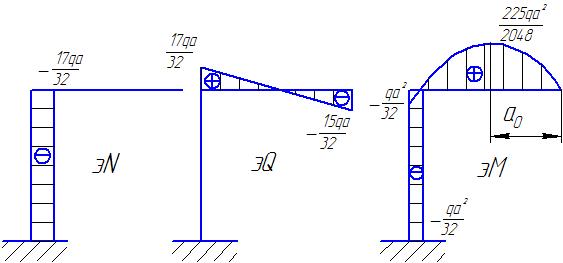
2. Строим эN, эQ, эМ:

На этом решение расчетно-графической работы № 2 заканчивается.

Расчетно-графическая работа № 3. Расчет статически неопределимых конструкций Задание 3.1. Статически неопределимые рамы.

Дана плоская статически неопределимая рама, на которую действует равномерно распределенная нагрузка, сосредоточенная сила и момент (рис. 3.1). Величины нагрузок и длины участков заданы в табл. 3.1.

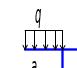
Рис. 3.1 Расчетные схемы рам

Табл. 3.1-Данные к заданию 3.1

	1	2	3	4	5	6	7	8	9	0	шифр
Схема	I	II	III	IV	V	VI	VII	VIII	IX	X	в
Р, кН	20	30	40	50	60	10	15	5	25	20	а
М, кН∙м	5	10	6	8	4	12	15	7	16	14	б
q, кН/м	10	8	9	10	12	14	15	20	22	18	в
а, м	1	0,9	0,8	0,7	2	0,5	1,5	1,6	1,8	2,5	а

Требуется:

1. Раскрыть статическую неопределимость тремя методами: Кастильяно, Мора, Верещагина.

2. Построить эпюры внутренних силовых факторов.

Пример:

На рис. П3.1 изображена плоская рама, на которую действует равномерно распределенная нагрузка q. Длины участков равны а. Рама имеет две опоры: шарнирно-подвижную и жесткую заделку.

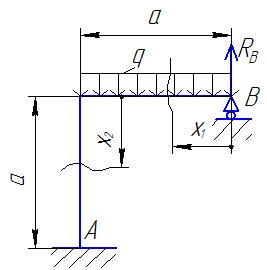
Рис. П3.1 Расчетная схема плоской статически неопределимой рамы

Решение:

1) Для раскрытия статической неопределимости используем уравнение:

Метод Кастильяно

,

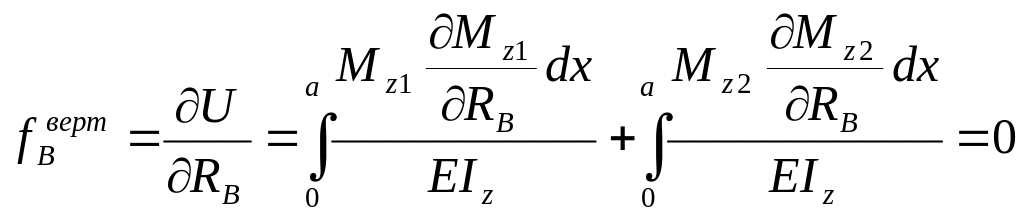где , ,

тогда , .

После интегрирования и сокращения переменных получаем:

, откуда .

Метод Мора

,

где, согласно рис. П3.1.1, моменты от единичной нагрузки будут равны, соответственно:

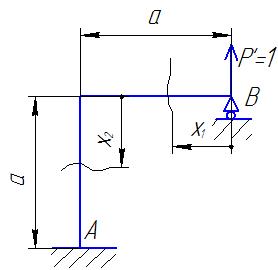
Рис. П3.1.1 Расчетная схема с единичной силой

, .

В этом случае, подынтегральная функция совпадает с выражением, полученным по методу Кастильяно, следовательно, ответ также получается равным .

Метод Верещагина

,

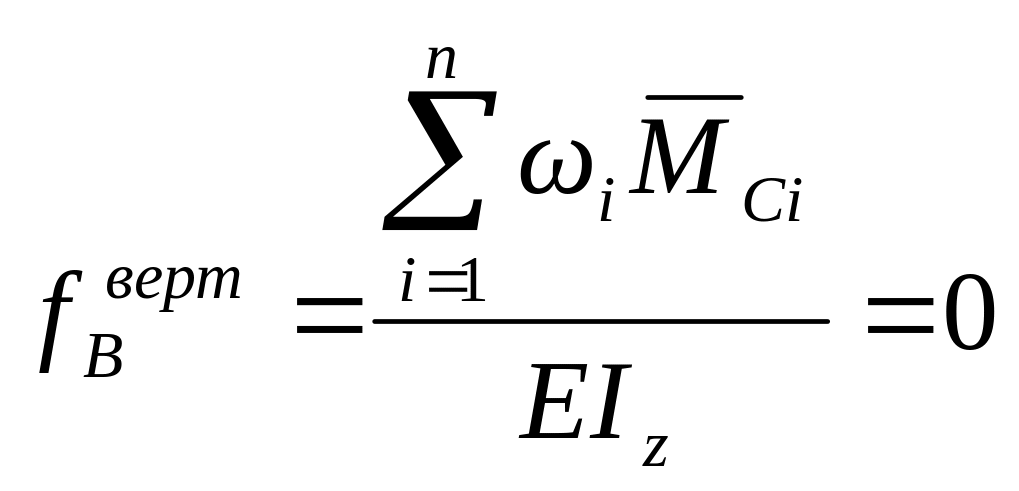где, согласно рис. П3.1.2 и рис. П3.1.3, имеем:

;

.

После сокращения, получаем:

,

В итоге, , что совпадает с двумя предыдущими методами.

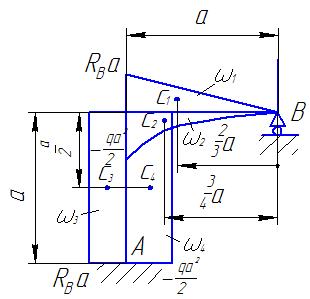
Рис. П3.1.2 Эпюра изгибающих моментов от внешней нагрузки

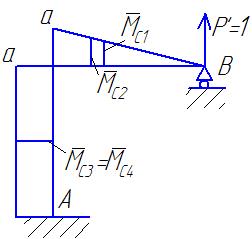
Рис. П3.1.3 Эпюра моментов от единичной силы

2. Определяем внутренние силовые факторы:

1-й участок (0≤х₁≤а)

;

; ; .

; ; .

Исследуем функцию изгибающего момента на экстремум:

, откуда , тогда .

2-й участок (0≤х₁≤а)

; ; .

Строим эN, эQ, эМ.