Задание 1.2. Статически неопределимые стержни.

Здесь необходимо рассчитать стержень из задания 1.1, который закреплен при помощи двух жестких заделок: в сечении 1 и дополнительно в сечении 4.

К примеру, стержень, изображенный на рис. П1.1, применительно к данной задаче, показан на рис. П1.2.

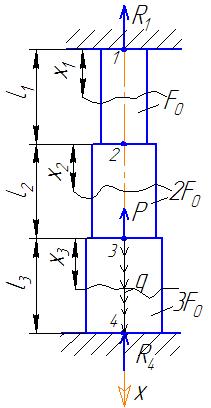
Рис. П1.2 Расчетная схема статически неопределимого стержня

Решение:

1) Записываем уравнение равновесия:

;

,

откуда

2) Составляем условие совместности деформаций

.

Распишем его по закону Гука

, откуда

.

Из уравнения равновесия находим

.

Дальнейший ход решения совпадает с заданием 1.1.

Задание 1.3. Статически неопределимые стержневые конструкции.

На рис. 1.2 изображена стержневая конструкция. Данные для этого задания имеются в табл. 1.2. Исключая нулевые стержни, получаем конструкцию, состоящую из 3-х стержней.

Рис. 1.2 Стержневая конструкция

Табл. 1.2-Данные к заданию 1.3

№ столбца

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

Данные

Углы наклона стержней

Абсолютно жесткий стержень

Нулевые стержни

Номер опорной точки и вид опоры

Номер стержня и его площадь

Величина, место приложения и направление силы

Номер стержня и его монтажная и температурная неточность

Обозначения

α

β

γ

–

li=0, где i=

–

–

–

–

–

–

P

∆

∆t

Размерность

град.

град.

град.

–

–

–

–

–

–

–

кН

–

мм

ºС

1

–

120

–

–

1,2,3,5,8,9,10, 11,12

4 F0

6 1,2F0

7 0,8F0

400

0 вниз

4 +0,10

7 +5

2

–

–

–

0-2

2,3,5,6,8,9,10, 11,12

1 2F0

7 1,6F0

–

600

0 вниз

1 +0,15

7 ­–5

3

–

–

–

0-5

2,3,5,6,8,9,10, 11,12

1 1,1F0

4 2,5F0

–

200

0 вниз

1 +0,20

4 +10

4

90

140

–

0-2

1,2,3,7,8,9,10, 11,12

5 0,4F0

6 0,9F0

–

300

0 вправо

5 +0,06

6 –10

5

90

–

–

2-1-0-6

4,6,8,9,10,11,12

5 0,4F0

7 0,8F0

–

400

0 вниз

5 –0,15

7 +20

6

90

–

–

2-3-0-6

2,3,4,6,8, 10,11

–

7 0,3F0

9 F0

–

500

6 вниз

7 –0,15

9 –20

7

–

–

45

2-1-0-6

4,5,6,7,9, 10

–

11,12 0,5F0

8 0,8F0

–

600

6 вверх

8 –0,20

8 +30

8

110

–

70

1-0-3-4-5

1,3,4,6,7, 12

–

8 0,9F0

9 1,1F0

–

700

1 вниз

8 –0,25

9 –30

9

120

–

–

3-0-6

1,2,3,4,5,6,7,8, 10,11

9 F0

12 1,1F0

–

800

6 вниз

9 +0,05

12 +40

0

–

–

–

–

1,3,5,6,8,9,10,11 12

2 F0

4 1,5F0

7 0,8F0

900

0 влево

2 –0,05

7 –40

шифр

в

в

в

в

в

в

в

в

в

в

в

в

в

в

в

Примечание: Длины l₁, l₂, l₃ и материал стержней взять из табл. 1.1.

Требуется:

1. Составить расчетные схемы силовой, монтажной и температурной задачи.

2. В каждой задаче раскрыть статическую неопределимость при помощи уравнения, составленного из условия совместности деформаций.

3. Выполнить расчет на прочность.

Пример:

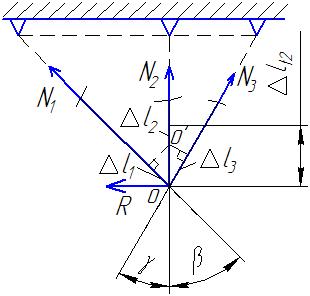
Пусть дана конструкция состоящая из 3-х деформируемых стержней (рис. П1.3). Сила Р = 100 кН, высота l = 1 м, углы β = 45˚, γ = 30˚, соотношения площадей F₁ = F₃ = F₀, F₂ = 2F₀, [σ] = 140 МПа. В монтажной задаче неточность изготовления стержня 1 составляет Δ₁ = +0,2 мм. В температурной задаче стержень 2 охлажден на величину Δt₂ = -10˚С.

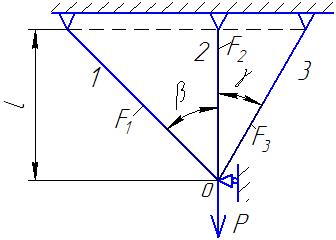
Рис. П1.3 Схема стержневой конструкции.

Решение:

Силовая задача

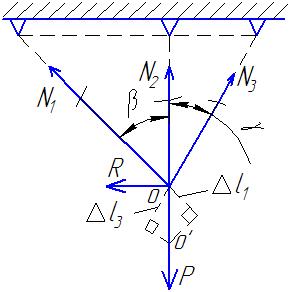1. С оставляем уравнения равновесия:

Из суммы сил на вертикальную ось, имеем –

. (а)

2. Записываем условия совместности перемещений:

.

Распишем перемещения по закону Гука

,

после сокращения, получим:

. (б)

Решая совместно (а) и (б), находим усилия в стержнях:

N₁ = 16,6 кН; N₂ = 66,6 кН; N₃ = 24,9 кН.

3. Определяем напряжения в стержнях:

; ; .

4. Выполняем расчет на прочность:

.

Таким образом, допускаемая площадь поперечного сечения составит

.

На этом решение заканчивается.

Монтажная задача

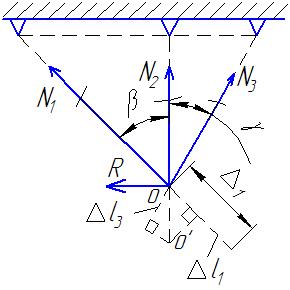
1. Составляем уравнения равновесия:

Из суммы сил на вертикальную ось, имеем –

.

2. Записываем условия совместности деформаций:

.

Далее ход решения совпадает с силовой задачей.

Температурная задача

1) Составляем уравнения равновесия:

Из суммы сил на вертикальную ось, вновь имеем –

.

2) Записываем условия совместности деформаций:

,

где , для стали, коэффициент линейного расширения составляет .

Далее ход решения совпадает с двумя предыдущими задачами.

На этом расчетно-графическая работа № 1 заканчивается.