Завдання 3 Необхідно розрахувати значення коригуючого множника z2

Приклад роз’язання: Використовуючи дані попереднього прикладу, розрахувати коригуючий множник 1/Z₂ при річній простій дисконтній ставці, що використовується банком для обліку векселів d = 11,5%.

З а формулою (2.15):

Тоді коригуючий множник .

Очевидно, що при інших рівних умовах Z₁ > Z₂, a .Тобто при використанні варіанта, коли відсотки нараховуються на залишок заборгованості, ціна товару потребуває меншого коригування.

Методи визначення оптимального співвідношення процентної і облікової ставок

Визначення оптимального співвідношення відсоткової і облікової ставок при розрахунку вексельних сум, дозволяє уникнути процедури коригування ціни товару.

У випадку, коли відсотки нараховуються на залишок заборгованості, із формули (11) випливає, що при Z₁ = 1, значення А = Р. Отже:

. (2.16)

Звідси, оптимальне значення облікової і відсоткової ставок за період t визначається, відповідно:

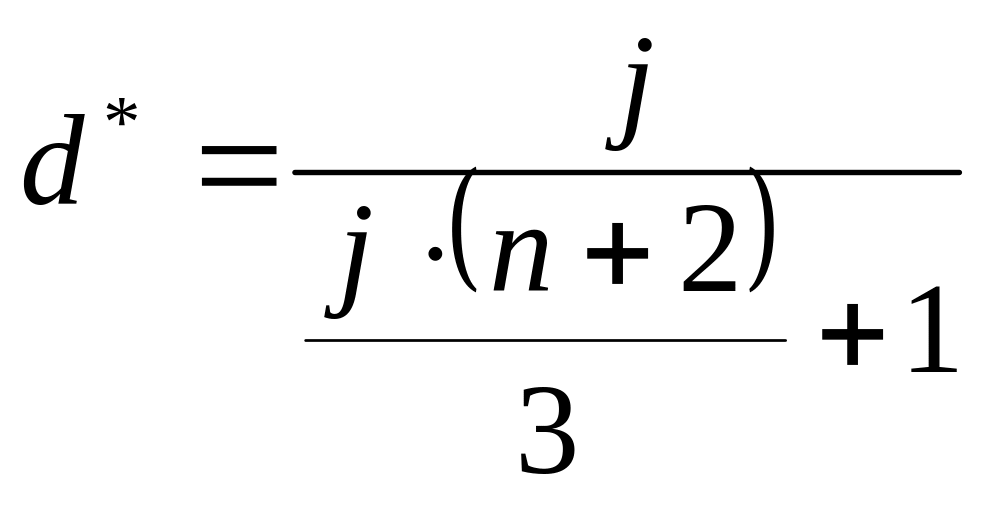, (2.17) і

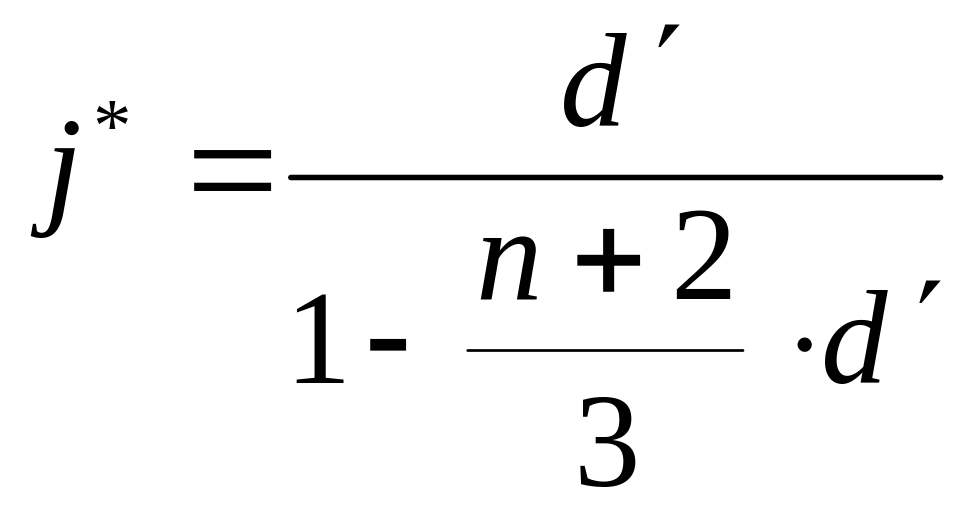. (2.18)

При використанні d^* і j^* продавець, після урахування векселів, одержує суму, не меншу, попередньо узгодженій ціні товару.

Завдання 4 Розрахувати суму, отриману дисконтуванням векселів по оптимальній обліковій ставці d*

Приклад роз’язання: Використовуючи дані попереднього прикладу, розрахувати суму, отриману дисконтуванням векселів по оптимальній обліковій ставці d^*.

За формулою (2.17) визначаємо оптимальну облікову ставку (у розрахунку на півріччя):

.

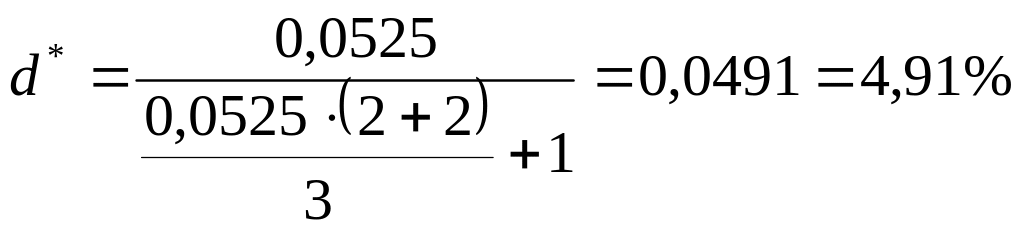Таблиця 2.3 Суми, отримані дисконтуванням векселів по оптимальній обліковій ставці d^*.

Період погашення векселя (t)	Сума векселя (Vt), тис. Грн	Сума, отримана продавцем після дисконтування векселів по оптимальній ставці d* = 0,0455, тис. грн
1	0,304	0,304 · (1 – 1 · 0,0491) = 0,289
2	0,289	0,289 · (1 – 2 · 0,0491) = 0,261
Всього	0,593	0,55

У випадку, коли відсотки нараховуються на суму боргу, включену у вексель:

. (2.19)

Звідси, оптимальне значення облікової і відсоткової ставок за період t визначається, відповідно:

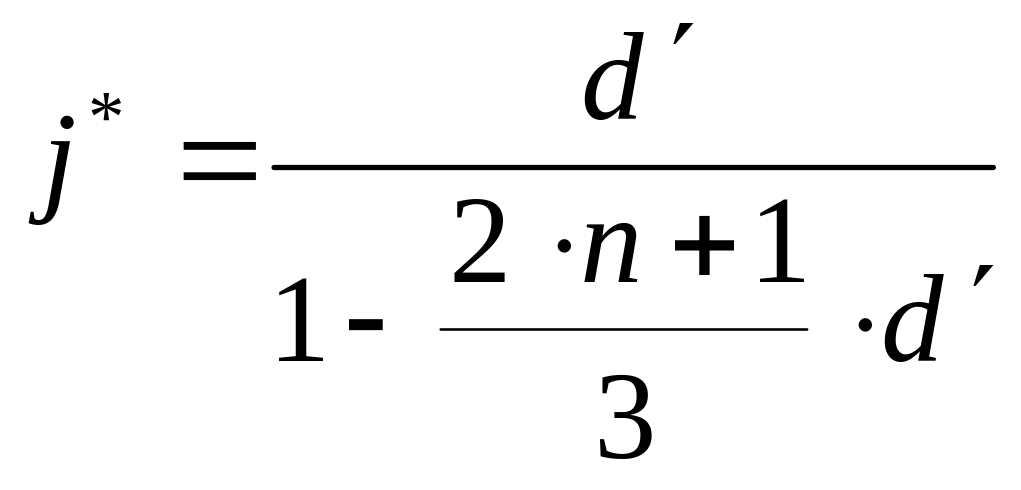, (2.20)

і

. (2.21)

Завдання 5 Розрахувати суму, отриману дисконтуванням векселів по оптимальній обліковій ставці j*.

Приклад роз’язання: Використовуючи дані попереднього прикладу, розрахувати суму, отриману дисконтуванням векселів по оптимальній відсотковій ставці j^*.

За формулою (2.20) визначаємо оптимальну відсоткову ставку (у розрахунку на півріччя):

.

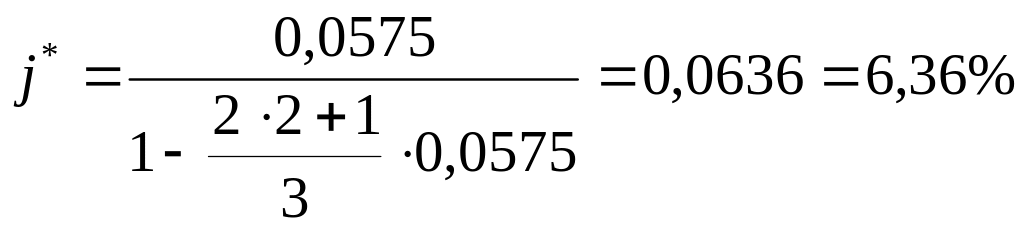Таблиця 2.4 - Суми, отримані дисконтуванням векселів по оптимальній процентній ставці j^*.

Період погашення векселя (t)	Сума погашення основного боргу (P/n), тис. грн.	Платежі відсотків(It, тис. Грн	Сума векселя (Vt), тис. грн	Сума, отримана продавцем після дисконтування векселів по оптимальній відсотковій ставці = 0,055, тис. грн
1	5,0	0,33	5,33	5,33 (1 – 1 · 0,055) = 5,04
2	5,0	0,66	5,66	5,66·(1 – 2 · 0,055) = 5,04
Всього	20,0	3,3	23,3	20,00131