Вариант 1

1. Для задачи распределительного типа построить модель линейного программирования.

Фирма Nike&Sons производит товар 4 видов, для производства которых необходимы 3 ресурса. Возможный объем потребления первого, второго и третьего ресурсов в месяц ограничены неотрицательными величинами , и . Расход -ого ресурса для производства единицы товара - ого вида описан в таблице:

	Расход ресурса на 1 ед. товара
	товар 1-го вида	товар 2-го вида	товар 3-го вида	товар 4-го вида
Ресурс 1	3	2	2	4
Ресурс 2	10	5	12	4
Ресурс 3	8	7	4	10

Прибыль с единицы товара первого, второго, третьего и четвертого вида составляет: 11, 8, 13, 9 условных единиц. Необходимо определить объем , , и производимых соответственно видов товаров в месяц, обеспечивающих максимальную суммарную прибыль.

2. Решить задачу графически:

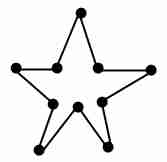
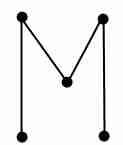
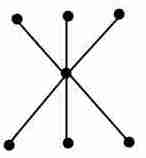
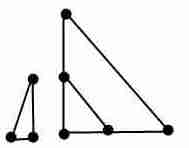
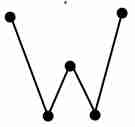
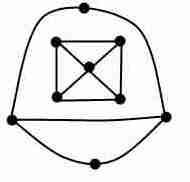
3. Укажите степени вершин. Является ли граф: 1. связным графом 2. графом содержащим циклы, 3. графом одна из компонент связности, которого является полным графом 4. Деревом

4. Осуществите обход деревьев и обозначьте номер посещаемой вершины, при обходе по уровням слева направо (справа налево) и в глубину слева направо (справа налево).

5. Построить таблицу истинности для данной формулы

Ф =

6. Доказать равносильность формул используя основные равносильности.

и

Вариант 2

1. Для задачи распределительного типа построить модель линейного программирования.

Фирма Jon&Sons производит товар 3 видов, для производства которых необходимы 3 ресурса. Возможный объем потребления первого, второго и третьего ресурсов в месяц ограничены неотрицательными величинами , и . Расход -ого ресурса для производства единицы товара - ого вида описан в таблице:

	Расход ресурса на 1 ед. товара
	Ресурс 1	Ресурс 2	Ресурс 3
товар 1-го вида	3	2	2
товар 2-го вида	10	5	12
товар 3-го вида	8	7	4

Прибыль с единицы товара первого, второго, третьего и четвертого вида составляет: 11, 8, 9, условных единиц. Необходимо определить объем , , производимых соответственно видов товаров в месяц, обеспечивающих максимальную суммарную прибыль.

2. Решить задачу графически:

3. Укажите степени вершин. Является ли граф: 1. связным графом 2. графом содержащим циклы, 3. графом одна из компонент связности, которого является полным графом 4. Деревом

4. Осуществите обход деревьев и обозначьте номер посещаемой вершины, при обходе по уровням слева направо (справа налево) и в глубину слева направо (справа налево).

5. Построить таблицу истинности для данной формулы

Ф =

6. Доказать равносильность формул используя основные равносильности.

и

Вариант 3

1. Для задачи распределительного типа построить модель линейного программирования.

Фирма Davis&Sons оказывает услуги 3 видов, для осуществления которых необходимы 4 ресурса. Возможный объем расхода первого, второго, третьего и четвертого ресурсов в неделю ограничены величинами , , и . Расход -ого ресурса для оказания одной услуги - ого вида описан в таблице:

	Расход ресурса на одну услугу
	1-ая услуга	2-ая услуга	3-ая услуга
Ресурс 1	4	5	9
Ресурс 2	3	6	1
Ресурс 3	7	8	2
Ресурс 4	11	12	8

Прибыль оказания услуги первого, второго, третьего и четвертого вида составляет: 110, 80, 130 условных единиц. Необходимо определить объем , , оказываемых соответственно видов услуг в неделю, обеспечивающих максимальную суммарную прибыль.

2. Решить задачу графически:

3. Укажите степени вершин. Является ли граф: 1. связным графом 2. графом содержащим циклы, 3. графом одна из компонент связности, которого является полным графом 4. Деревом

4. Осуществите обход деревьев и обозначьте номер посещаемой вершины, при обходе по уровням слева направо (справа налево) и в глубину слева направо (справа налево).

5. Построить таблицу истинности для данной формулы

Ф =

6. Доказать равносильность формул используя основные равносильности.

и