10. Принятие характеристики усилительного элемента нелинейной
Все реальные системы являются нелинейными.
Вместо коэффициента внешней обратной связи KИ2 примем нелинейный элемент - идеальное двухпозиционное реле.
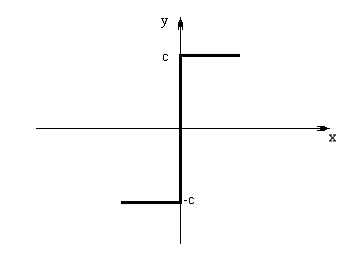
Рисунок 16. Характеристика нелинейного элемента
Гармонический
коэффициент линеаризации: q(a) =
;
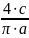С – параметр нелинейного элемента. Примем с = 1.
11. Составление структурной схемы нелинейной системы, получение передаточной функции линейной части системы
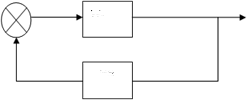
Рисунок 17. Структурная схема НСАР
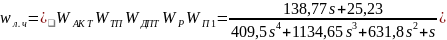
12. Исследование методом гармонической линеаризации нсар
Используя критерий Михайлова найдем параметры автоколебаний: амплитуду и частоту.
Характеристическое уравнение системы имеет следующий вид:
=
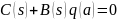
S заменим на jw
|
|
|
|
|
|
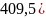
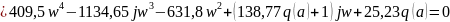
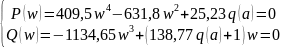
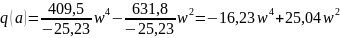
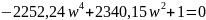
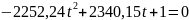
D=5484608 T1=-0.0004
T2=1.0395
– частота
автоколебаний.
;
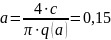
Проверим систему на устойчивость по критерию Михайлова.
Для
оценки устойчивости предельного цикла
зададим приращение амплитуды
:
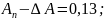
Рассчитаем
значения
в этих точках:
q1=7,49
q2=9,79
>> w=0:0.01:10;
>> q=8.501;
>> P=409.5*w.^4-631.8*w.^2+25.23*q;
>> Q=-1134.65*w.^3+138.77*w*q+w;
>> q1=7.49;
>> P1=409.5*w.^4-631.8*w.^2+25.23*q1;
>> Q1=-1134.65*w.^3+138.77*w*q1+w;
>> q2=9.79;
>> P2=409.5*w.^4-631.8*w.^2+25.23*q2;
>> Q2=-1134.65*w.^3+138.77*w*q2+w;
>> plot(P, Q, P1, Q1, '--', P2, Q2, ':')
Годограф с положительным приращением амплитуды автоколебаний изображен символами ‘--’, с отрицательными приращениями – ‘-.‘.
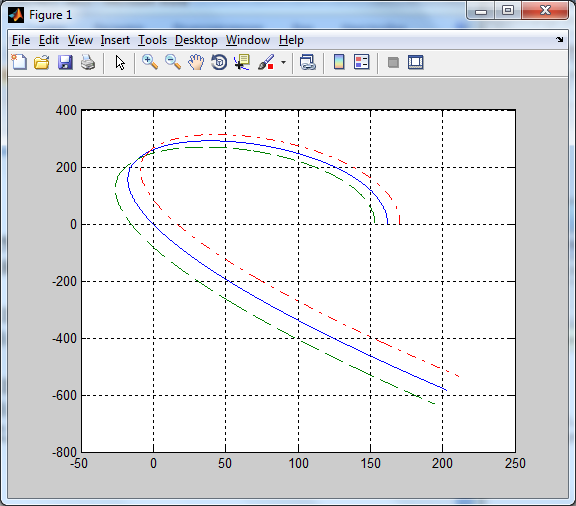
Рисунок 18. Годограф Михайлова с приращениями амплитуды автоколебаний
Предельный цикл является устойчивым (автоколебания существуют), т.к. при положительном приращении амплитуды годограф проходит правее вектора М, а при отрицательном приращении - левее.
Нелинейная система устойчива в «большом», но неустойчива в «малом».
13. Запись пф дсар
Реализуем математическую модель ДСАР. Для перехода от непрерывной модели к дискретной воспользуемся функцией С2D .
Определим период квантования по теореме Котельникова.
C этой целью построим амплитудно-частотную характеристику передаточной функции замкнутой системы по задающему воздействию:
Рисунок 19. АЧХ ПФ замкнутой системы по задающему воздействию
Определим период квантования по теореме Котельникова:
,
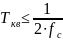либо
.
с.
Примем
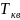равным 5 секундам.
>> Wg=tf([1942.81 353.24],[409.5 1134.65 631.8 70.39 12.62])
Transfer function:
1943 s + 353.2
---------------------------------
409.5 s^4 + 1135 s^3 + 631.8 s^2 + 70.39 s + 12.62
>> Wgd=c2d(Wg,5,'zoh')
Transfer function:
12.25 z^3 + 3.607 z^2 - 3.44 z - 0.02086
-----------------------------------------------------
z^4 - 1.239 z^3 + 0.7107 z^2 - 0.02838 z + 9.622e-007
Sampling time: 5