3. Условия максимизации прибыли фирмы-монополиста

Предположим, что структура издержек фирмы-монополиста задана кривыми АТС и МС и ТС, а предельный доход определяется кривой спроса. Каковы будут оптимальные уровни цен и объема монополиста?

В условиях совершенной конкуренции текущая цена устанавливается рынком, и фирма не может воздействовать на нее, являясь ценополучателем. Для максимизации прибыли (или минимизации своих потерь, если получение прибыли невозможно) фирма должна определить оптимальный в данных рыночных и технологических условиях объем выпуска. При чистой монополии фирма может максимизировать прибыль, выбирая либо соответствующий объем, либо цену.

Два подхода к определению условий максимизации

Существует два уже известных нам взаимосвязанных подхода к определению условий максимизации прибыли.

1. Метод совокупных издержек  совокупного дохода.

Совокупная прибыль фирмы максимизируется при таком объеме выпуска, когда разница между ТR и ТС будет максимально большой:

max п = TR -TC

Рис. 3. Определение максимального уровня прибыли

На рис. 3 видно, что монополист будет получать экономическую прибыль в любой точке отрезка АВ, но максимальная прибыль может быть получена лишь в точке, где касательная к кривой ТС имеет тот же наклон, что и кривая ТR. Функция прибыли находится путем вычитания ТС из ТR для каждого объема производства. Пик кривой совокупной прибыли (п) показывает оптимальный объем производства, т.е. объем, максимизирующий прибыль в краткосрочном периоде.

Необходимое условие максимизации прибыли можно записать следующим образом: Совокупная прибыль достигает своего максимума при объеме производства, при котором предельная прибыль равна нулю.

Мп=0.

Предельная прибыль (Мп)  прирост совокупной прибыли при изменении объема выработки на единицу. Геометрически предельная прибыль равна наклону функции совокупной прибыли и подсчитывается по формуле

Мп=(п)`=dп/dQ.

Если Мп>0, то функция совокупной прибыли растет, и дополнительное производство может увеличить совокупную прибыль. Если же Мп<0, то функция совокупной прибыли уменьшается, и дополнительный выпуск сократит совокупную прибыль. И только при Мп=0 значение совокупной прибыли максимально.

Из необходимого условия максимизации (Мп=0) вытекает второй метод.

2. Метод предельных издержек  предельного дохода.

Мп=(п)`=dп/dQ,

(п)`=dTR/dQ-dTC/dQ.

А поскольку dTR/dQ=MR, а dTC/dQ=МС, то совокупная прибыль достигает своего наибольшего значения при таком объеме выпуска, при котором предельные издержки равны предельному доходу: МС=МR.

Если предельные издержки больше предельного дохода (МC>МR), то монополист может увеличить прибыль за счет сокращения объема производства. Если предельные издержки меньше предельного дохода (МC<МR), то прибыль может быть увеличена за счет расширения производства, и лишь при МС=МR в точке Q* достигается равновесие, как это представлено на рис. 4.

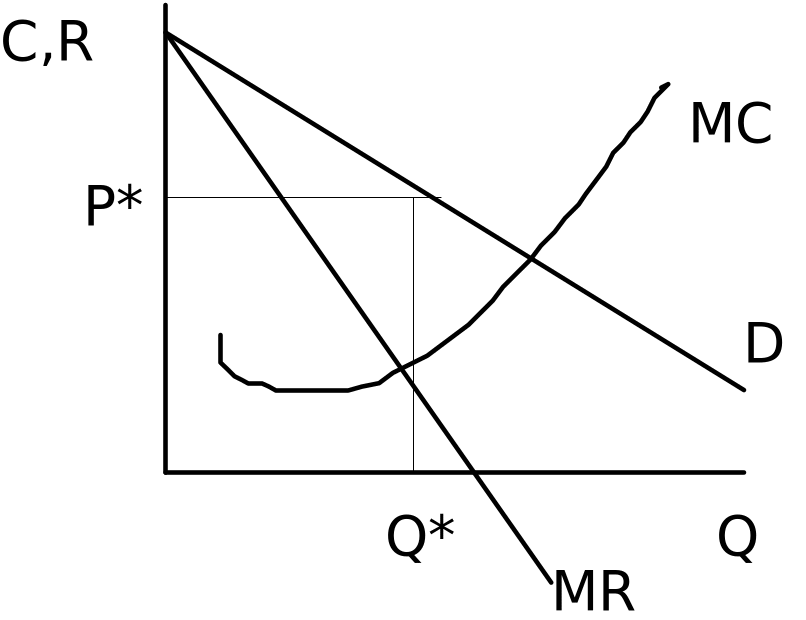
Рис. 4. Условие экономического равновесия

Равенство MC=MR является условием максимизации, а не условием минимизации прибыли лишь в том случае, когда выполняется условие второго порядка:

п``(Q)=TR``(Q)-TC``(Q)<0

или поскольку MR(Q)=TR`(Q), а MC(Q)=TC`(Q),

то MR`(Q)-MC`(Q)<0.

Графически это означает, что кривая предельного дохода пересекает кривую предельных издержек сверху вниз (рис. 4). В противном случае равенство MR=MC будет минимизировать прибыль (рис. 5).

Рис. 5. Условие минимизации прибыли

Пример 1. Нахождение оптимального объема производства фирмы-монополиста.

Известно, что функция спроса монополиста имеет вид Р=5000-17Q, функция совокупных издержек TC=75000+200Q-17Q²+Q³.

Определить:

1. объем производства, обеспечивающий фирме максимальную прибыль;

2. оптимальную рыночную цену;

3. величину совокупной прибыли.

Решение:

Условием максимизации прибыли является равенство MC=MR. Найдем МС и MR из данных уравнений:

1. TR=PQ=(5000-17Q)Q=5000Q-17Q²;

MR=(TR)`=dTR/dQ=5000-34Q;

2. MC=(TC)`=200-34Q+3Q²;

3. MC=MR;

200-34Q+3Q²=5000-34Q;

3Q²=4800; Q= - 40 Q=40.

Поскольку отрицательное значение не имеет экономического смысла, то оптимальный объем производства Q*=40.

Оптимальная рыночная цена находится путем подстановки Q* в функцию спроса.

4. P=5000-17Q;

P=5000-17(40)=4320 руб.

Совокупная прибыль может быть найдена как разница между TC и TR при Q*=40.

п=TR-TC=52000 руб.