Правила статистичної перевірки гіпотези

1. Задають малим числом >0, яке називається рівнем значущості критерію; зазвичай  = 0,05; 0,01 або 0,001. Воно характеризує ймовірність помилки першого роду.

2. Визначають критичну множину S за умови виконання нерівності

. (20)

3. Умовою (20) критична множина S визначається неоднозначно. Вибирають ту з можливостей, яка забезпечує мінімум імовірностей помилки другого роду, або, що те саме, максимум потужності критерію.

4. Проводять випробування та одержують значення критерію. Якщо при цьому настає подія {X  S}, то основна гіпотеза H₀відкидається. У противному разі вважають, що H₀не суперечить експериментальним даним. Результат перевірки гіпотези формулюють: гіпотеза H₀відкидається (не відкидається) на рівні значущості .

1.16. Критерій згоди 2

Критерії, які призначено для перевірки гіпотези про закон розподілу випадкової величини, називаються критеріями згоди. Нехай основна гіпотеза H₀ полягає в тому, що функція розподілу випадкової величини  є функція F(x).

Поділемо числову вісь на r проміжків (розрядів)

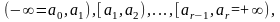
де 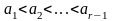. При вірній гіпотезі H₀ i–му розряду 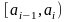відповідає ймовірність

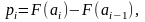
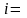1, 2, …, .

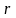З n вибіркових значень (Х₁, Х₂, …, Х_п) випадкової величини  до i-го розряду попадає випадкова кількість m_iзначень 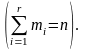Тоді відношення m_i/ n до ймовірностей p_iстверджуєосновну гіпотезу H₀, помітна різниця відкидає гіпотезу H₀. Випадкова величина

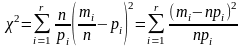(21)

характеризує погодженість гіпотези H₀з експериментальними даними. Критерій ²застосовують згідно із загальним правилом перевірки гіпотез. При цьому значення критерію обчислюють за формулою (21), критичну множину вибирають у вигляді напівскінченного інтервалу 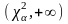, де величину 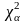знаходять за табл. 7 (див. дод. 2). Входами таблиці є величина  = r–1та рівень значущості .

Якщо виконується співвідношення > , то гіпотеза H₀відкидається на рівні значущості . У протилежному випадку вона не суперечить експериментальним даним.

Зауваження 1. Кількість вибіркових значень m_i, i=1 , 2,…, r у кожному розряді має бути не менше 5…10. Якщо ця умова не виконується, рекомендують об’єднувати розряди.

Зауваження 2. Критерій згоди ² можна застосувати не тільки, коли гіпотетичну функцію розподілу F(x) випадкової величини  повністю визначено. Якщо вона залежить від l невідомих параметрів, тобто має вигляд F (х; ₁, ₂, …, _l) та параметри ₁, ₂, …, _lвизначають за вибіркою методом максимальної правдоподібності (див. п.1.13), то критерій згоди залишається спроможним. У цьому випадку степінь вільності обчислюють за формулою  = r – l – 1 (табл. 7, дод. 2).

2. Теоретичні питання

1. Події. Правила дій над подіями.

2. Класичне, геометричне і статистичне означення ймовірності. Аксіоми Колмогорова.

3. Теорема додавання ймовірностей.

4. Умовна ймовірність. Формула множення ймовірностей. Парна незалежність подій і незалежність у сукупності.

5. Формула повної ймовірності. Формула Байєса.

6. Схема незалежних випробувань. Формула Бернуллі.

7. Локальна теорема Муавра–Лапласа.

8. Перша та друга модель Пуассона.

9. Випадкова величина. Функція розподілу одновимірної випадкової величини. Властивості.

10. Дискретні і неперервні випадкові величини. Числові характеристики. Властивості. Приклади.

11. Багатовимірна випадкова величина. Функція розподілу та щільність розподілу і щільність розподілу ймовірностей двовимірної випадкової величини. Властивості.

12. Числові характеристики двовимірної випадкової величини. Коваріація, коефіцієнт кореляції.

13. Двовимірний та багатовимірний нормальний розподіл.

14. Характеристична функція випадкової величини. Властивості.

15. Функціональне перетворення випадкових величин. Розподіл функції, числові характеристики.

16. Композиція законів розподілу випадкових величин. Лінійні перетворення багатовимірної нормальної випадкової величини.

17. Центральна гранична теорема. Інтегральна теорема Муавра Лапласа.

18. Закон великих чисел. Теорема Бернуллі. Нерівність Чебишова.

19. Основні статистичні розподіли: нормований нормальний, ², Стьюдента, F–розподіл.

20. Теорема про

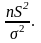
21. Вибіркові характеристики. Властивості.

22. Точкові оцінки параметрів розподілу. Метод максимальної правдоподібності.

23. Довірчі інтервали, довірчі ймовірності. Приклади.

24. Статистична перевірка гіпотез, критерії. Рівень значущості. Критична область. Помилки першого та другого роду.

25. Критерій знаків. Критерій грубих помилок спостережень.

26. Перевірка гіпотези про закон розподілу. Критерій згоди. Критерій ² (Пірсона). Критерій Колмогорова.