1.10. Числові характеристики випадкових величин
Нехай випадкова величина = () є функцією випадкової величини . Якщо потрібно визначити лише числові характеристики випадкової величини , можна не знаходити її закон розподілу. Числові характеристики виражають через закон розподілу випадкового аргумента. Якщо має щільність розподілу p(x), то математичне сподівання М і дисперсія D дорівнюють відповідно
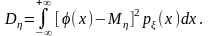
1.11. Закон великих чисел
Під законом великих чисел розуміють ряд теорем, поєднаних ідеєю стійкості середніх результатів за великої кількості випробувань.
Теорема Чебишова.Нехай випадкові величини 1, 2, …,n– незалежні і Di c, і = 1,2,…, де с – деяка стала. Тоді для кожного > 0 виконується граничне співвідношення
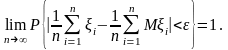(13)
Теорема Маркова. Нехай
випадкові величини 1,
2,
…,n,…
задовольняють умови
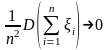при n.
Тоді для кожного >
0 виконується граничне
співвідношення (13).
Теорема Бернуллі. Нехай m – кількість успіхів у n незалежних випробуваннях, р – ймовірність успіху у кожному випробуванні. Тоді для кожного > 0
Доведення цих теорем базується
на нерівності Чебишова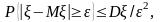
що має місце для кожного >
0 та кожної випадкової
величини, яка має скінченне математичне
сподівання М
і скінченну дисперсію D.
1.12. Центральна гранична теорема для однаково розподілених випадкових доданків
Нехай
1,
2,
…,n,
… - незалежні однаково
розподілені випадкові величини, що
мають математичне сподівання Мi
= a і
скінченну дисперсію Di
= 2.
Тоді при n
функція розподілу нормованої суми
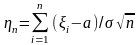збігається до функції розподілу
нормальної випадкової величини з
параметрами (0,1), тобто для кожного x
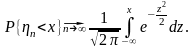
Звідси одержуємо наближену формулу
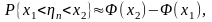
що здійснюється при достатньо великих n. Вона виражає ймовірність виконання нерівності x1<n<x2через інтеграл імовірності (4) (див. табл. 2, дод. 2).
1.13. Точкові оцінки параметрів розподілу
Вибіркою називається n–вимірна випадкова величина (X1, X2, …, Xn) з незалежними однаково розподіленими компонентами Xi, і = 1, 2,…n. Число n називається об’ємомвибірки.
Довільна функція h=h (X1, X2, …, Xn) вибіркових значень називається статистикою.
Нехай – невідомий параметр розподілу випадкової величини . Статистика
* = * (X1, X2, …, Xn), (14)
яку використовують у наближеній рівності , називається оцінкою (точковою оцінкою) невідомого параметра.
Класифікація оцінок. Бажано, щоб оцінка (14) не давала систематичного завищення або заниження результатів, тобто щоб М* (X1, X2, …, Xn)= .
Оцінка, що має зазначену властивість, називається незсуненою. В іншому випадку вона називається зсуненою.
Якщо при n оцінка * збігається за ймовірністю до справжнього значення параметра :
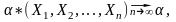
то оцінка * називається спроможною. Спроможність означає, що зі збільшенням об’єму вибірки якість оцінки поліпшується.
Якщо оцінки 1* і 2* задовольняють нерівність М (1* – )2 < M (2* – )2, то оцінка 1* називається більш ефективною, ніж 2*. Якщо є оцінка *— більш ефективна, ніж довільна інша, то вона називається ефективною.
Методи одержання оцінок. 1. Метод моментів. Нехай – неперервна випадкова величина з щільністю розподілу p(x, ), що залежить від одновимірного невідомого параметра . Тоді математичне сподівання М є функцією :
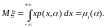
Вибіркове
середнє
набуває значення, близьке до М.
Це дає змогу записати рівняння для
визначення невідомого параметра :
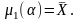
Метод моментів аналогічно застосовують до дискретних випадкових величин.
2. Метод максимальної правдоподібності. Нехай – дискретна випадкова величина з розподілом
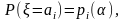i
= 1, 2, …, k,
де
ai
– можливі значення випадкової величини
;
pi()
– відповідні ймовірності, що залежать
від невідомого параметра ,
причому
для довільного припустимого .
Множина значень ai випадкової величини може бути не тільки скінченною, але й зліченною.
Якщо серед вибіркових значень (x1, x2, …, xn), число aiтрапляєтьсяni разів (i= 1, 2, …, n), то для ймовірності L(x1, x2, …, xn;) одержання даної вибірки маємо вираз:
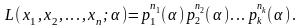(15)
Функція (15) параметра називається функцією правдоподібності, а величина *, за якої функція L(x1, x2, …, xn;) набуває максимального значення, – оцінкою максимальної правдоподібності невідомого параметра .
Для неперервної випадкової величини зі щільністю розподілу p(x,), що залежить від невідомого параметра , метод максимальної правдоподібності залишається спроможним. Відмінність полягає в тому, що тепер функцію правдоподібності L (х1, х2, …, хn; ) = р(х1, ) р(х2, ) ... p(хn, ) виражають не через імовірність одержання даної вибірки, а через щільність розподілу n–вимірної випадкової величини (X1, X2, …, Xn), що залежить від параметра . При цьому є аргументом, значення x1, x2, …, xnвважають фіксованими.