1.7. Закони розподілу і числові характеристики випадкових величин

Випадковою величиною  називається функція (), яку позначено на просторі елементарних подій  яка задовольняє умови вимірності відносно -алгебри подій, тобто для кожного дійсного x множина {:()<x} належить -алгебрі подій і, таким чином, має імовірність.

Функцією розподілу випадкової величини називається функція змінної x, що дорівнює

F(х)=P {<x}, –<x<.

Тобто значення функції розподілу F(х) випадкової величини  є імовірність того, що  одержує значення менше за x.

Випадкова величина  називається дискретною, коли є скінченна або зліченна множина чисел х₁, х₂, ..., х_k, ..., таких, що

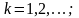
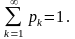
Сукупність значень хk і відповідних ймовірностей pk називається розподілом дискретної випадкової величини.

Приклади дискретних розподілів

1. Біноміальний розподіл:

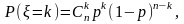
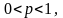1, 2, ..., .

2. 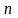Розподіл Пуассона:

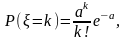
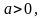0, 1, 2, ... .

3. Геометричний розподіл:

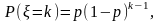1, 2, ... .

4. Гіпергеометричний розподіл:

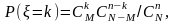0, 1, 2, ...

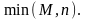
Випадкова величина  називається абсолютно неперервною випадковою величиною, якщо її функцію розподілу може бути подано у вигляді

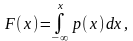(7)

де р(х) – деяка інтегрована на (–,) функція, яка називається щільністю розподілу випадкової величини. Можна показати, що р(х) – невід’ємна функція і така, що

Приклади неперервних розподілів

1. Рівномірний розподіл:

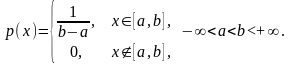
2. Нормальний розподіл (з параметрами a, ):

3. Показниковий (експоненціальний) розподіл:

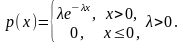
4. Розподіл Коші:

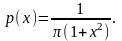
Із формули (7) випливає, що в кожній точці неперервності р(х) маємо рівність

.

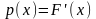Математичним сподіванням дискретної випадкової величини  називається число

. (8)

Якщо випадкова величина набуде зліченної множини значень, то необхідна абсолютна збіжність ряду (8). Якщо ряд не збігається, то випадкова величина не має математичного сподівання.

Математичним сподіванням неперервної випадкової величини називається число

якщо інтеграл збігається абсолютно.

Дисперсією D випадкової величини  називається математичне сподівання випадкової величини(—M)²:

Для дискретної випадкової величини дисперсію обчислюють за формулою

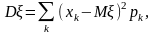
а для неперервної – за формулою:

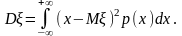
Імовірність того, що випадкова величина  набуває значення у заданому числовому проміжку, обчислюють за однією з формул:

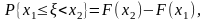
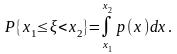
Двовимірні випадкові величини

Розподіл двох випадкових величин  і , або двовимірної випадкової величини (, ), не вичерпується розподілом кожної з них, оскільки при цьому не враховується залежність, яка може бути між ними.

Функцію розподілу F(x,y) двовимірної випадкової величини (, ) позначають, як імовірність сумісного виконання нерівностей <x і <y:

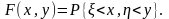
Якщо F(x,y) може бути подано у вигляді F(x, у)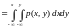 , де p(x,y) – деяка інтегрована невід’ємна функція, то двовимірну випадкову величину (, ) називають неперервною, а функцію p(x,y) – щільністю розподілу двовимірної випадкової величини (, ).

Щільність розподілу p_(x) випадкової величини  виражають через сумісну щільність p(x,y) так:

Аналогічно для щільності розподілу випадкової величини  маємо:

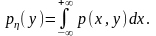
На відміну від сумісної щільності розподілу p(x,y), одновимірні щільності p_(x) і p_(x) називають маргінальними.

Випадкові величини  і  називаються незалежними, якщо їх сумісна функція розподілу F(x,y) при довільних значеннях аргументів x, y дорівнює добутку маргінальних функцій розподілу F_(x) випадкової величини  і F_(x)випадкової величини :

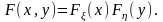
Нехай (, ) – неперервна двовимірна випадкова величина зі щільністю розподілу p(x,y).Тоді для незалежності  і  необхідно і достатньо, щоб сумісна щільність p(x,y)розкладалася у добуток маргінальних щільностейp_(x) і p_(x):

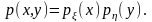
Коефіцієнт кореляції. ВеличинаМ [( – М) ( – М)]називаєтьсяковаріацією випадкових величині, cov(, ). Якщо (, ) – неперервна двовимірна випадкова величина з щільністю розподілу p(x,y), то

cov () =

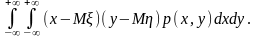
Величина r = cov(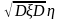, )/ називається коефіцієнтом кореляціївипадкових величині .