МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ УКРАЇНИ

«КИЇВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ»

ТЕОРТЕОРІЯ ЙМОВІРНОСТІ, ІМОВІРНІСНІ ПРОЦЕСИ ТА МАТЕМАТИЧНА СТАТИСТИКА

Методичні вказівки до виконання

розрахунково-графічної роботи

Для студентів напряму підготовки

6.050101 «Комп’ютерні науки»

Кафедра автоматизованих систем обробки інформації і управління

всіх форм навчання

Рекомендовано

Вченою радою факультету

Інформатики та обчислювальної

техніки НТУУ «КПІ»

Протокол № 12 від 28.05.2012 р.

Київ

НТУУ «КПІ»

2012

Теорія ймовірностей, імовірнісні процеси та математична статистика. Методичні вказівки до виконання розрахунково-графічної роботи / Уклад.: В.М. Кузнецов – К.: НТУУ «КПІ». 2012. – 80с.

Методичнівказівкипризначені для студентів напряму підготовки 6.050101 «Комп’ютерні науки» кафедри автоматизованих систем обробки інформації і управління всіх форм навчання. В документі наведено довідковий теоретичний матеріал, теоретичні питання для перевірки знань, задачі та додатки з вихідними даними по варіантах і таблицями розподілів, що використовуються для розв’язання задач.

Укладач:В.М.Кузнецов, к.ф.-м.н., доцент

Відповідальний редактор О.Г. Жданова, к.т.н., доцент

Рецензент Ю.О. Кулуков, д.т.н., професор

За редакцією укладачів

Зміст

1. доВідковий теоретичний матеріал 5

1.1. Класичне означення ймовірності 5

1.2. Елементи комбінаторики 5

1.3. Геометричне означення ймовірності 7

1.4. Теорема додавання і формула множення ймовірностей 7

1.5. Формула повної імовірності, формула Байєса 8

1.6. Схема незалежних випробувань Бернуллі 8

1.7. Закони розподілу і числові характеристики випадкових величин 10

Приклади дискретних розподілів 11

Приклади неперервних розподілів 11

Двовимірні випадкові величини 13

Властивості коефіцієнта кореляції 15

Властивості математичного сподівання і дисперсії 15

1.8. Характеристичні функції 15

Властивості характеристичних функцій 16

1.9. Закони розподілу функцій випадкових аргументів 17

1.10. Числові характеристики випадкових величин 19

1.11. Закон великих чисел 19

1.12. Центральна гранична теорема для однаково розподілених випадкових доданків 20

1.13. Точкові оцінки параметрів розподілу 21

1.14. Довірчі інтервали 23

Приклади довірчих інтервалів 23

1.15. Статистична перевірка гіпотез 25

Правила статистичної перевірки гіпотези 26

1.16. Критерій згоди ² 27

2. Теоретичні питання 28

3. ЗАДАЧІ 30

Додатки 40

Додаток 1 40

Додаток 2 63

ЛІТЕРАТУРА 75

1. ДоВідковий теоретичний матеріал

1.1. Класичне означення ймовірності

Імовірністю події А у схемі скінченної кількості однаково можливих елементарних подій називається відношення

,

де m(A) – кількість елементарних подій, що сприяють події А; n – загальна кількість елементарних подій.

1.2. Елементи комбінаторики

Припустимо, що необхідно виконати послідовно k дій. Коли першу дію можна виконати n₁ способами, другу – n₂способами, третю – n₃способами і так до k-ї дії, яку можна виконати n_kспособами, то всі k дій разом можна виконати n₁ n₂ n₃n_k способами, у цьому полягає основний принцип комбінаторики (правило множення).

Нехай  – деяка множина з n елементів. Деяка k-елементна підмножина множини з n елементів називається комбінацією з n елементів по k. Порядок елементів у підмножині не є істотним. Кількість k-елементних підмножин множини позначають .

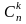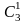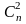Наприклад, коли  = {а, b, с}, тоді {а}, {b}, {с} – усі можливі комбінації з 3 по 1 (отже, =3); {а, b}, {а, с}, {b, с} — усі можливі комбінації з 3 по 2 (отже, =3).

Кількість комбінацій з n елементів по k обчислюють за формулою

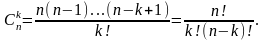
Множину називають упорядкованою, коли кожному елементу цієї множини відповідає деяке число (номер елемента) від 1 до n (n – кількість елементів множини), де різним елементам відповідають різні числа.

Різноманітні упорядковані множини, що відрізняються лише порядком елементів (тобто можна одержати з тієї самої множини), називають перестановками цієї множини. Наприклад, перестановки множини  = {а, b, с} мають вигляд:

{a, b, c}, {a, c, b}, {b, a, c},

{b, c, a}, {c, a, b}, {c, b, a}.

Кількість перестановок Р_n множини, що містить n елементів, обчислюють за формулою Р_n = n!.

Розглянемо упорядковані підмножини даної множини . Кожну її підмножину може бути упорядковано деяким можливим способом. Кількість усіх k-елементних підмножин множини  дорівнює . Кожну таку підмножину можна упорядкувати k! способами. Таким чином, одержуємо всі упорядковані k-елементні підмножини множини . Кількість упорядкованих k-елементних підмножин множини, що містить n елементів, позначають через

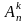
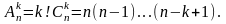
Упорядковані k-елементні підмножини множини з n елементів називаються розміщеннямзnелементів поk. Різні розміщення з n по k відрізняються або елементами, або їх порядком.

Нехай k₁, k₂, … k_m– цілі невід’ємні числа, причому Подамо множину А з nелементів у вигляді суми m множин А₁, А₂, ..., А_m,що містять відповідно k₁, k₂, … k_mелементів. Позначимо кількість різних способів такого розбиття на групи через (k₁, k₂, ..., k_m). Її обчислюють за формулою:

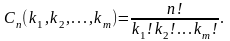
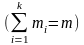Наведемо комбінаторну схему, що зустрічається при розв’язуванні задач: n-елементна множина А є сумою множин А₁, А₂, ..., А_k, кількість елементів яких дорівнює відповідно п₁, п₂ ..., п_k В – m-елементна підмножина множини А, що містить т₁елементів з A₁, m₂з A₂, ..., т_k елементів з А_k . Кількість способів, якими можна вибирати таку множину В з А (множини неупорядковано), за основним принципом комбінаторики дорівнює