2.4.5 Восьмерично–двоичные преобразования. Преобразование смешанного восьмеричного числа в двоичную систему счисления.

Из разложений 1.6 и 1.7 вытекает следующий алгоритм конвертации восьмеричного числа в двоичную систему счисления.

1. Каждая цифра восьмеричного числа заменяется соответствующей двоичной комбинацией (триадой) по таблице соответствия (см. Пример 16.)

2. Положение запятой и знак числа – сохраняются.

П ример 17. Преобразовать восьмеричное число XQ= 25,247Q в двоичную систему счислении. Формализованная запись задания 025,247Q → XB

Метод преобразования в этом случае поясняется рисунком

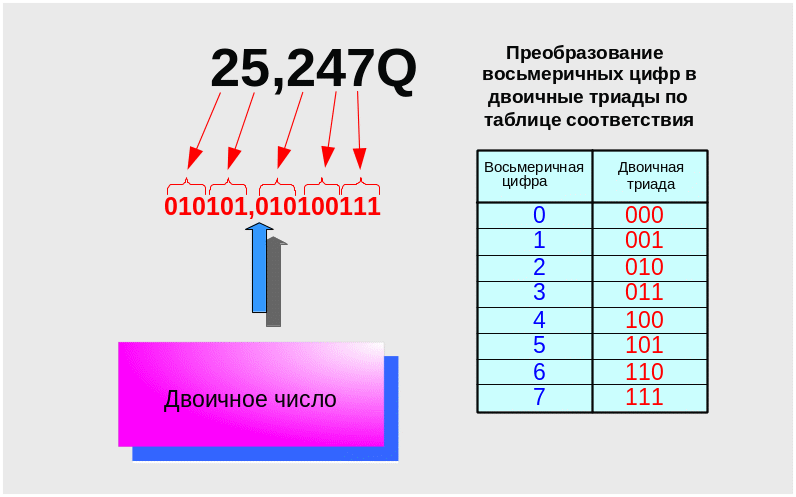
Таким образом, восьмеричное число 25,247Q после преобразования в двоичную систему счисления имеет вид 010101,010100111B.

Двоично-шестнадцатеричные и шестнадцатерично-двоичные преобразования

2.4.6 Преобразование целой части двоичного числа в шестнадцатеричную систему счисления.

Преобразования основаны на разложении вида

XB =( a _n-1*2 ³+ a _n-2*2 ²+a _n-2*2 ¹+ a _n-3*2 ⁰)*(2⁴) ^N-1+…

…+( a ₃*2³+ a ₂*2 ²+a₁*2 ¹+ a ₀*2⁰)* (2⁴)⁰ (1.8)

где N – разрядность целой части шестнадцатеричного числа

n – разрядность целой части двоичного числа

Из (1.8) следует следующий алгоритм преобразования

1. Целая часть числа разбивается на группы из четырех разрядов (тетрады) Разбиение начинается с младшего разряда (“справа налево”).

2. Если в старшей тетраде менее, чем четыре цифры , то вместо отсутствующих цифр записывают нули, которые дополняют тетраду до полной

3. Комбинация цифр в каждой тетраде рассматривается как целое число, которое заменяется соответствующей шестнадцатеричной цифрой.

4. П олученное число - целое число в шестнадцатеричной системе счисления.

П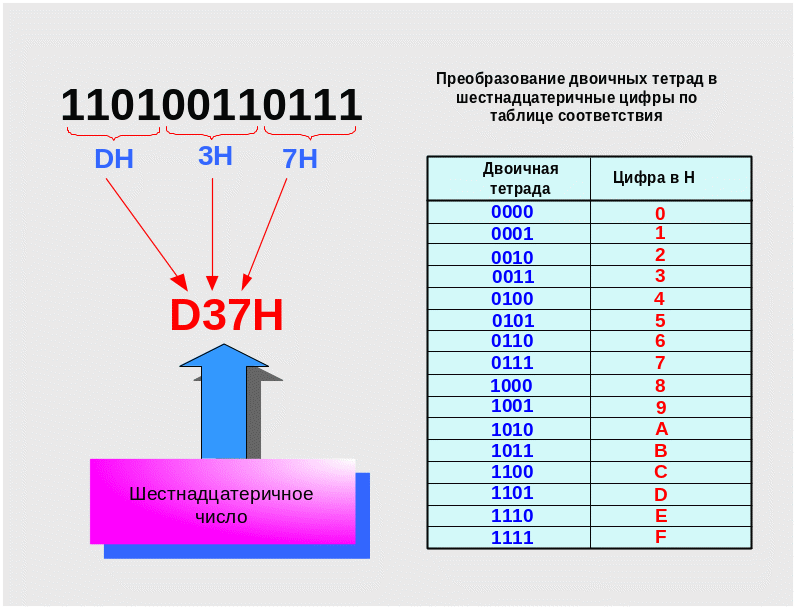 ример 18. Преобразовать двоичное целое число X₂= 110100110111В в шестнадцатеричную систему счисления. Формализованная запись задания 110100110111В → XH.

2.4.7 Преобразование дробной части двоичного числа в шестнадцатеричную систему счисления.

Преобразования основаны на разложении вида

XB = ( a_-1*2 ³+a _-2* 2²+ a _-3*2 ¹ + a _-4*2⁰ )*(2⁴)^-1+…

…+( a_-m+3*2 ³+ a_-m+2*2 ²+a _-m+1*2 ¹+ a _-m*2⁰)* (2⁴)^-M, (1.9)

где M – разрядность дробной части шестнадцатеричного числа

m – разрядность дробной части двоичного числа

Из разложения (1.9) следует следующий алгоритм преобразования

1. дробная часть исходного числа разбивается на группы из четырех разрядов (тетрад). Разбиение начинается со старшего разряда дробной части (“слева направо”).

2. Если в младшей тетраде менее, чем четыре цифры , то она дополняется справа нулями до полной тетрады

3. Комбинация цифр в каждой тетраде рассматривается как целое двоичное число и заменяется соответствующей шестнадцатеричной цифрой.

4. П олученное число - дробное двоичное число в шестнадцатеричной системе счисления.

Пример 19. Преобразовать двоичного числа XB= 0,0100110111В шестнадцатеричную систему счислении. Формализованная запись задания 0,0100110111В → XQ.

Метод преобразования в этом случае поясняется рисунком.

Нетрудно заметить из рисунка, что младшая тетрада исходного двоичного числа дополнена до полной тетрады двумя нулями.

Таким образом, применение алгоритма приводит к результату 0,0100110111В = 0,4DCH