Значения и
Вариант |
Массив значений
наработки до отказа
|
Заданное значение
|
Значение , |
1 |
2 |
3 |
4 |
1 |
21, 18, 12, 11, 18, 12, 19, 18, 13, 8, 14, 26, 21, 11, 17, 19, 23, 18, 12, 18, 16, 19, 11, 7, 13, 16, 9, 20, 22, 17, 19, 12, 9, 19, 17, 22, 21, 11, 18, 17, 18, 21, 20, 8, 18, 15, 17, 13, 16, 25 |
18,5 |
8,0 |
2 |
3, 18, 19, 3, 8, 7, 16, 19, 11, 4, 15, 14, 19, 3, 5, 8, 10, 9, 16, 17, 18, 11, 15, 15, 18, 14, 11, 15, 7, 8, 13, 17, 13, 12, 9, 5, 8, 11, 17, 14, 18, 11, 9, 16, 14, 18, 11, 13, 17, 4 |
10,5 |
5,5 |
3 |
11, 16, 12, 14, 13, 27, 21, 22, 20, 12, 16, 14, 15, 16, 19, 10, 13, 15, 14, 16, 18, 19, 11, 11, 13, 17, 15, 16, 14, 17, 18, 19, 21, 15, 16, 19, 12, 13, 17, 15, 14, 18, 10, 11, 17, 18, 15, 19, 21, 19 |
14,0 |
8,5 |
4 |
11, 18, 16, 28, 14, 16, 15, 22, 14, 16, 15, 16, 16, 15, 11, 13, 11, 19, 10, 19, 10, 15, 17, 8, 19, 16, 16, 12, 9, 14, 12, 15, 17, 12, 14, 15, 19, 19, 21, 13, 14, 18, 10, 15, 17, 9, 13, 12, 12, 14 |
15,5 |
7,5 |
5 |
19, 19, 17, 14, 19, 21, 16, 13, 18, 11, 12, 17, 16, 17, 14, 15, 16, 13, 15, 21, 21, 15, 18, 13, 17, 18, 13, 16, 17, 14, 16, 17, 11, 17, 19, 15, 14, 17, 18, 19, 18, 13, 16, 15, 13, 17, 12, 11, 13, 17 |
13,0 |
4,5 |
6 |
17, 16, 18, 19, 21, 15, 11, 17, 14, 18, 15, 19, 13, 16, 18, 18, 15, 21, 20, 19, 17, 18, 11, 10, 19, 16, 19, 16, 11, 10, 11, 8, 18, 19, 16, 20, 22, 27, 15, 27, 11, 13, 18, 18, 11, 15, 16, 17, 17, 15 |
14,5 |
6,0 |
7 |
15, 12, 12, 15, 11, 11, 10, 17, 15, 18, 17, 16, 19, 13, 15, 16, 15, 17, 11, 17, 18, 19, 12, 16, 15, 16, 18, 18, 19, 20, 11, 10, 18, 15, 18, 18, 13, 13, 17, 27, 29, 21, 26, 27, 21, 11, 8, 18, 18, 17 |
17,0 |
6,5 |
8 |
16, 12, 19, 11, 17, 19, 20, 21, 19, 18,17, 16, 19,18, 1, 17,19, 16, 18, 16, 19, 20, 21, 18, 21, 18, 18, 15, 16, 13, 13, 13, 13, 17, 18, 18, 18, 21, 18, 18, 19, 20, 22, 27, 28, 28, 11, 17, 17, 13 |
18,0 |
9,0 |
9 |
17, 16, 12, 18, 19, 11, 10, 17, 20, 22, 28, 26, 25, 13, 17, 18, 19, 21, 20, 27, 27, 11, 18, 18, 19, 21, 13, 18, 29, 8, 19, 17, 19, 29, 18, 26, 15, 25, 24, 11, 18, 16, 18, 13, 17, 26, 22, 21, 20, 11 |
16,0 |
5,0 |
10 |
17, 18, 19, 20, 21, 22, 22, 23, 25, 24, 11, 12, 13, 14, 15, 15, 17, 16, 19, 18, 17, 12, 18, 17, 18, 11, 10, 17, 16, 15, 14, 13, 18, 19, 20, 20, 20, 20, 20, 12, 21, 28, 17, 18, 16, 15, 18, 13, 16, 17 |
17,5 |
9,5 |
11 |
14, 24, 23, 23, 17, 19, 17, 15, 16, 14, 19, 20, 21, 30, 12, 16, 13, 12, 15, 18, 28, 12, 18, 19, 20, 21, 25, 17, 18, 16, 19, 21, 16, 19, 13, 22, 23, 27, 18, 19, 11, 18, 19, 19, 28, 21, 28, 11, 28, 11 |
13,5 |
7,0 |
12 |
18, 16, 13, 17, 19, 20, 27, 26, 26, 21, 23, 25, 24, 21, 27, 23, 17, 18, 18, 18, 28, 23, 13, 17, 18, 16, 14, 16, 17, 28, 18, 19, 21, 20, 21, 22, 23, 10, 29, 14, 19, 18, 17, 15, 18, 16, 13, 18, 27, 11 |
15,0 |
10,0 |
13 |
29, 22, 27, 25, 18, 28, 11, 17, 16, 14, 16, 15, 13, 11, 12, 17, 19, 17, 20, 16, 18, 19, 12, 19, 20, 21, 28, 21, 28, 12, 19, 18, 19, 19, 21, 21, 20, 18, 14, 16, 16, 17, 13, 17, 18, 12, 19, 20, 16, 13 |
16,5 |
7,5 |
14 |
17, 18, 19, 19, 13, 17, 17, 18, 15, 19, 13, 12, 10, 11, 17, 17, 15, 18, 13, 16, 17, 19, 17, 20, 21, 22, 28, 22, 18, 19, 11, 16, 17, 18, 14, 16, 15, 17, 18, 16, 13, 18, 19, 12, 17, 18, 11, 18, 19, 20 |
18,5 |
9,5 |
15 |
29, 29, 26, 27, 21, 20, 27, 30, 37, 27, 18, 16, 29, 32, 31, 28, 38, 32, 4, 17, 18, 11, 18, 21, 20, 19, 29, 32, 21, 13, 17, 19, 19, 19, 21, 27, 17, 26, 21, 25, 28, 21, 28, 32, 32, 23, 23, 31, 20, 24 |
20,5 |
11,0 |
16 |
21, 20, 20, 26, 17, 18, 16, 15, 18, 16, 13, 17, 18, 21, 23, 17, 28, 13, 21, 17, 23, 32, 27, 18, 16, 18, 14, 18, 15, 18, 19, 13, 14, 15, 18, 16, 17, 15, 17, 19, 21, 20, 12, 17, 21, 17, 14, 32, 13, 18 |
16,5 |
8,5 |
17 |
20, 21, 22, 27, 18, 19, 17, 15, 18, 19, 17, 21, 17, 18, 19, 21, 18, 19, 21, 17, 28, 21, 21, 19, 21, 17, 15, 15, 13, 15, 12, 11, 10, 11, 19, 28, 19, 28, 21, 13, 13, 17, 18, 16, 19, 21, 17, 13, 18, 11 |
21,0 |
12,5 |
18 |
17, 32, 16, 18, 19, 21, 16, 13, 16, 23, 27, 17, 21, 18, 15, 18, 19, 12, 17, 18, 14, 16, 18, 19, 12, 16, 18, 19, 13, 17, 18, 21, 20, 22, 21, 25, 21, 20, 18, 19, 15, 18, 18, 19, 21, 19, 20, 21, 20, 11 |
19,0 |
10,5 |
19 |
19, 16, 17, 18, 13, 16, 18, 17, 16, 19, 20, 21, 18, 17, 15, 17, 18, 18, 13, 17, 18, 18, 20, 21, 20, 19, 19, 20, 18, 16, 17, 18, 18, 20, 21, 19, 19, 20, 20, 18, 18, 16, 18, 13, 14, 15, 16, 19, 23, 15 |
20,5 |
13,0 |
20 |
18, 17, 17, 18, 21, 19, 16, 18, 16, 19, 15, 18, 21, 22, 27, 25, 27, 18, 19, 18, 16, 15, 19, 21, 20, 21, 27, 16, 15, 19, 16, 19, 21, 27, 22, 29, 21, 28, 18, 19, 21, 15, 13, 14, 17, 18, 11, 12, 17, 19 |
20,0 |
13,5 |
,
,
Требуется определить
статистические вероятности безотказной
работы
и отказа
устройства для заданного значения
,
указанного в табл. 1. Далее необходимо
рассчитать значение вероятности
безотказной работы
по первым 20 значениям наработки до
отказа, указанным для соответствующего
варианта в таблице 1. Затем для заданной
наработки
требуется рассчитать математическое
ожидание числа работоспособных устройств
при общем числе находившихся в эксплуатации
устройств, указанном в таблице 2.
Таблица 2. Объем
партии устройств и заданное значение
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Объем партии |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
750 |
800 |
350 |
Значение |
2 |
3 |
5 |
6 |
4 |
2 |
8 |
5 |
7 |
3 |
Вариант |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Объем партии |
150 |
250 |
350 |
450 |
550 |
650 |
750 |
750 |
850 |
900 |
Значение |
4 |
3 |
5 |
6 |
8 |
5 |
8 |
4 |
7 |
2 |
Статистически вероятность безотказной работы устройства для наработки определяется как
,
где 
– число объектов, работоспособных на
момент времени
.
Вероятность отказа устройства за наработку статистически определяется как
,
где 
– число объектов, неработоспособных к
наработке
Поскольку
,
нетрудно заметить, чему равна сумма
вероятностей:
.
Произведем проверку правильности своих
вычислений:
Оценку вероятности
безотказной работы устройства по первым
20-ти значениям наработки до отказа
обозначим как
.
Ее значение определяется также по
формуле (1), но при этом
,
и число работоспособных объектов
выбирается из этой совокупности.
Тогда с учетом формулы (1) математическое ожидание числа объектов , работоспособных к наработке , определяется как
,
где 
– объем партии устройств, определяемый
по таблице 2.
Задание 2.
Требуется рассчитать среднюю наработку
до отказа
рассматриваемого устройства. Первоначально
вычисления произвести непосредственно
по выборочным значениям
,
указанным в таблице 1, а затем с
использованием статистического ряда.
Для вычислений
среднего значения
случайной величины
непосредственно по ее выборочным
значениям
используют формулу
.
Для выполнения
данного задания примем
ч, а
.
Случайная величина распределения в пределах от 7,5 ∙103 до 19,5 ∙103.
Расчет распределения случайной величины, т.е. момент отказа,
Нижнюю границу интервала =7,5∙103 ч установите, пользуясь таблицей 1.
Статистический ряд можно отразить графически, как показано на рисунке 1.
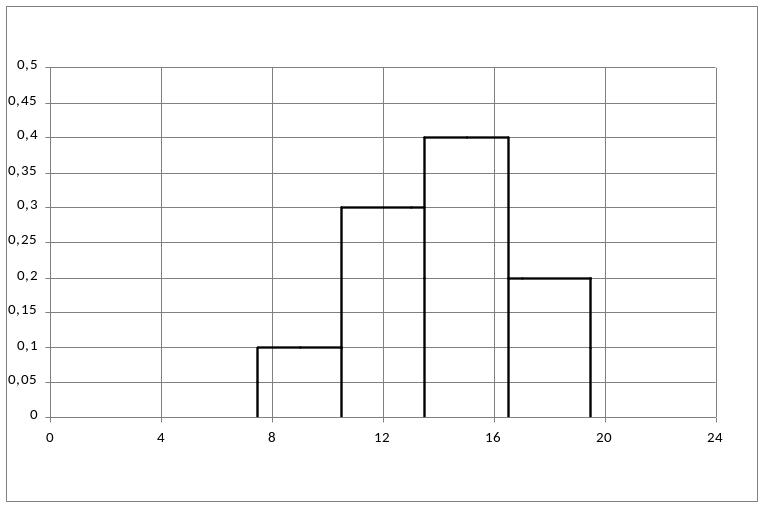
Рис. 1. Графическое представление статистического ряда
Таблица 3. Преобразование значений наработки до отказа в статистический ряд
|
Число попаданий на интервал |
|
Статистическая вероятность |
|
№ |
Нижняя и верхняя
границы,
|
|||
1 |
7,5 ÷ 10,5 |
|
n1=5 |
q1=0,1 |
2 |
10,5 ÷ 13,5 |
|
n2=15 |
q2=0,3 |
3 |
13,5 ÷ 16,5 |
|
n3=20 |
q3=0,4 |
4 |
16,5 ÷ 19,5 |
|
n4=10 |
q4=0,2 |
|
50 |
1 |
||
ч
Статистическая
вероятность
попадания случайной величины на
-ый
интервал рассчитывается как
Подсчитайте значения для всех разрядов и проверьте правильность расчетов, используя выражение
.
Для расчета среднего
значения случайной величины в качестве
«представителя» всех ее значений,
принадлежащих
-му
интервалу, принимают его середину
.
Тогда средняя наработка до отказа
определяется как
.
Расчет с использованием формулы (4) вносит некоторую методическую ошибку. Однако ее значение обычно пренебрежимо мало. Эту ошибку в Ваших расчетах оцените по формуле
,
где 
и
– средние значения, вычисленные
соответственно с использованием формул
(3) и (4).
Задание 3.
Требуется рассчитать интенсивность
отказов
для заданных значений
и
.
Интенсивность отказов рассчитывается по формуле:
,
где 
– статистическая вероятность отказа
устройства на интервале [
,
]
или иначе – статистическая вероятность
попадания на указанный интервал случайной
величины
;
[ = 15,5*103 ч, = 18,5*103 ч]
– рассчитанная на первом шаге I-вероятность безотказной работы устройства.
Вероятность безотказной работы блока
,
Средняя наработка блока до отказа находится как
.
При последовательном соединении блоков интенсивность отказов образуемой ими подсистемы:
.
Если интенсивности отказов всех блоков одинаковы, то интенсивность отказов подсистемы
,
а вероятность безотказной работы подсистемы
.
С учетом (7) и (8) средняя наработка подсистемы до отказа находится как
.
Результаты расчета погрешности блока и подсистемы сводим в таблицу 2:
t, ч |
800 |
1200 |
1600 |
2000 |
2400 |
2800 |
3200 |
3600 |
4000 |
4400 |
4800 |
5200 |
РБ(t) |
0,8325 |
0,7596 |
0,693 |
0,6323 |
0,5769 |
0,5264 |
0,4803 |
0,4382 |
0,3998 |
0,3648 |
0,3329 |
0,3037 |
Рп(t) |
0,5769 |
0,4382 |
0,3329 |
0,2528 |
0,192 |
0,1459 |
0,1108 |
0,0842 |
0,0639 |
0,0486 |
0,0369 |
0,028 |
Проверка результата расчета:
Вероятности безотказной работы подсистемы не отличаются друг от друга.
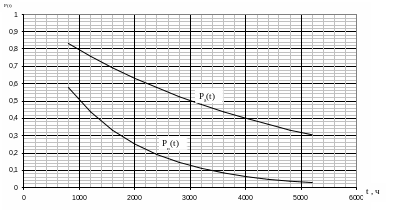
Рис.2. Зависимости Рδ(t) и Рп(t)
Задание 4.
Для наработки
требуется рассчитать вероятность
безотказной работы
системы (рис. 3), состоящей из двух
подсистем, одна из которых является
резервной.
Система