III Примеры решения задач и тесты с комментариями, определяющими правильные ответы на них Оглавление

Основные понятия механики материалов: Закон Гука. Диаграмма растяжения 2

Методы определения механических свойств материалов, 6

макро- и микротвeрдость материалов 6

Биомеханика зубо-челюстной системы 9

Теплофизические характеристики материалов 13

Механические колебания и волны. Акустика. УЗИ 15

Физические основы гидро- и гемодинамики 20

Элементы физики поверхностных явлений, адгезия 25

Физические процессы в клеточных мембранах: транспорт молекул и ионов через мембраны, мембранные потенциалы клетки 27

Физические основы электрографии органов и тканей, электрокардиография 33

Электрические и магнитные свойства тканей организма. Эквивалентная электрическая схема живой ткани. Зависимость импеданса живой ткани от частоты переменного тока 35

Электростимуляция тканей и органов, параметры импульсных сигналов, используемых при электростимуляции 37

Воздействие высокочастотных токов и полей на организм. Изучение методов и аппаратуры для высокочастотной терапии 39

Термоэлектрические явления, их использование в датчиках температуры. Изучение электрических датчиков температуры 42

Усиление биоэлектрических сигналов, частотная и амплитудная характеристики усилителя 46

Методы получения поляризованного света. Использование поляризационных методов для исследования биологических объектов 47

Законы поглощения и рассеяния света. Основы фотоколориметрии 53

и спектрофотометрии 53

Тепловое излучение тел. Энергетические характеристики теплового излучения. Тепловидение в медицине 56

Излучение и поглощение энергии атомами и молекулами. Люминесценция 60

и еe характеристики 60

Принцип действия лазера. Свойства лазерного излучения. 61

Применение лазеров в медицине 61

Рентгеновское излучение, его свойства и использование в медицине 62

Основные понятия механики материалов: Закон Гука. Диаграмма растяжения

1. Деформация называется упругой, если она:

a) сохраняется после прекращения действия внешней силы;

b) частично исчезает после прекращения действия внешней силы;

c) полностью исчезает после прекращения действия внешней силы;

d) является деформацией растяжения или сжатия.

Деформацию называют упругой, если после снятия нагрузки тело полностью восстанавливает свою форму и размеры. По этой причине упругую деформацию называют обратимой. Упругая деформация полностью исчезает после прекращения действия внешней силы.

2. Деформация называется пластической, если она:

a) полностью или частично сохраняется после прекращения действия внешней силы;

b) полностью исчезает после прекращения действия внешней силы;

c) мгновенно возрастает под действием внешней силы и затем сохраняет постоянное значение;

d) уменьшается со временем по экспоненциальному закону после прекращения действия внешней силы.

Деформацию называют пластической (неупругой), если размеры тела восстанавливаются не полностью, т.е. имеет место остаточная деформация. По этой причине пластическую деформацию называют необратимой. Пластическая деформация полностью или частично сохраняется после прекращения действия внешней силы.

3. Из теории упругости известно, что разнообразные виды деформации твердого тела могут быть сведены к двум основным, а именно к следующим:

a) деформации изгиба и деформации сдвига;

b) деформации растяжения и деформации кручения;

c) деформации растяжения (сжатия) и деформации сдвига;

d) деформации изгиба и деформации кручения.

Основные виды деформации твердых тел – это:

всестороннее сжатие;

одноосное сжатие (растяжение);

изгиб;

сдвиг;

кручение.

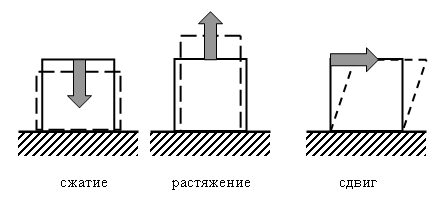
В теории упругости показано, что разнообразные виды деформации могут быть сведены к двум основным: растяжению (сжатию) и сдвигу. Они показаны на рисунках. Деформируемым образцом является прямоугольная призма из некоторого материала, закрепленная одной гранью. Направление действующей внешней силы указано на рисунке стрелкой. Пунктир соответствует деформированному образцу.

4. Укажите правильную формулировку закона Гука, определяющего связь между механическим напряжением и его относительной деформацией:

a) при упругой деформации механическое напряжение, возникающее в теле, пропорционально квадрату относительной деформации;

b) при упругой деформации механическое напряжение зависит от формы деформируемого тела;

c) при пластической деформации механическое напряжение увеличивается с течением времени;

d) при упругой деформации механическое напряжение, возникающее в теле, прямо пропорционально его относительной деформации.

При деформации в образце возникают внутренние упругие силы, препятствующие внешней нагрузке и дальнейшей деформации образца. Наличие в деформируемом образце упругих сил обусловливает возникновение в нем механических напряжений. Гук установил, что при упругих деформациях механическое напряжение, возникающее в теле, прямо пропорционально его относительной деформации. Это положение в теории упругости известно как «Закон Гука».

5. Установите соответствие между физической величиной и еe определением:

Предел пропорциональности		максимальное механическое напряжение, при котором деформация еще остаeтся упругой
Предел упругости		механическое напряжение, начиная с которого деформация возрастает практически без увеличения напряжения
Предел текучести		максимальное механическое напряжение, после которого деформируемое тело начинает необратимо разрушаться
Предел прочности		максимальное механическое напряжение и деформация связаны законом Гука

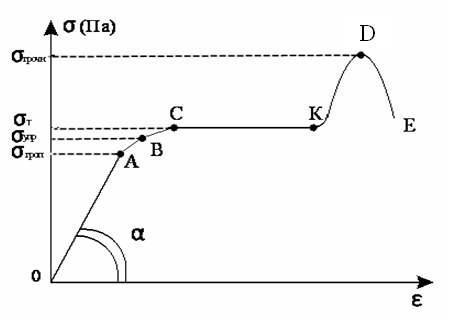
Зависимость между механическим напряжением в образце из определенного материала и его относительной деформацией обычно представляется диаграммой растяжения. Она отражает все особенности механического поведения материала. Рассмотрим диаграмму растяжения для типичного пластичного материала (см. рисунок), здесь  – механическое напряжение,  – относительная деформация.

На участке ОАВ деформация является упругой, но зависимость между  и  на участке АВ становится нелинейной, поэтому точке А соответствует предел пропорциональности – это максимальное напряжение, до которого  и  связаны законом Гука.

Точке В соответствует напряжение, называемое пределом упругости , поскольку при деформация становится неупругой (пластичной).

На участке СК относительная деформация образца растет при почти постоянном механическом напряжении, поэтому его называют участком текучести.

Точке С соответствует предел текучести.

Точке D соответствует предел прочности – это максимальное механическое напряжение, после которого деформируемое тело начинает необратимо разрушаться.

6. Установите соответствие между явлениями, характеризующими механическое поведение полимерных материалов, и их названиями:

Уменьшение механического напряжения со временем при постоянной деформации		механическая анизотропия
Различие механических свойств биотканей в различных направлениях		релаксация напряжения
Увеличение деформации со временем при постоянном механическом напряжении		ползучесть (крип)

Механическое поведение конкретного полимерного материала определяется тем, в каком физическом состоянии он находится в температурном интервале эксплуатации: (обычно -40…+ 40°С) вязкотекучем, высокоэластическом, кристаллическом или стеклообразном.

Полимеры, находящиеся в высокоэластическом состоянии, называются эластомерами. Для них характерны большие упругие (высокоэластические) деформации, достигающие сотен процентов.

Именно они находят широкое применение в стоматологии и характеризуются важными для практики временными эффектами:

а) при фиксированной величине деформации в образце из некоторого материала со временем происходит релаксация (уменьшение, спад механического напряжения);

б) при фиксированной нагрузке (механическом напряжении) со временем растет величина деформации – это явление называют ползучестью (или крипом).

Механическая анизотропия – различие механических свойств в различных направлениях

7. На рисунке представлена диаграмма растяжения некоторого материала. Предел текучести этого материала равен … МПа.

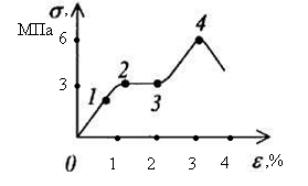
С учетом ответа на вопрос № 5 предел текучести соответствует точке 2 на графике, т.е. предел текучести этого материала составляет 3 МПа.

8. Модуль упругости хряща при сжатии равен 24 МПа, при сдвиге 80•10⁵Па. Определить коэффициент Пуассона для этой ткани. Можно ли хрящ считать несжимаемым материалом?

Коэффициент Пуассона , который зависит только от свойств материала деформируемого тела, определяет относительное изменение его объема при деформации. Если μ=0,5, то материал считается несжимаемым. Модуль сдвига G связан модулем упругости E соотношением: . Откуда можно получить формулу для определения : и сделать вывод относительно хряща.

9. Предел прочности губчатой составляющей нижней челюстной кости равен 16 Н/мм². Модуль упругости 210³ Н/мм². Если допустить применимость закона Гука, то максимальная возможная деформация для этой ткани составляет … %.

При одноосном растяжении закон Гука имеет вид: σ = E·ε, где σ – механическое напряжение; Е – модуль упругости материала; ε – относительное удлинение (ε=Δl/l), часто называемое относительной деформацией.

Выразим относительное удлинение ε через остальные параметры: . Подставим данные из условия задачи в последнюю формулу и полученный результат умножим на 100, чтобы получить ответ в процентах.