Тема 1.2. Сигналы электросвязи и их спектры.

1.Класификация сигналов электросвязи.

2.Параметры аналоговых и цифровых сигналов.

3.Переодические сигналы и их спектры.

4.Непериодические сигналы и их спектры.

1. Электрические сигналы по форме бывают следующих видов:

а) Аналоговые (непрерывные) – это такие сигналы, у которых в заданном интервале времени можно отсчитать бесконечно большое число значений. К таким сигналам относятся телефонные, вещательные, телевизионные, факсимильные. Телефонный сигнал (речевой) – получен путем преобразования создаваемого при устной речи звукового давления. Вещательные сигналы получены в результате преобразования звуков вещательных передач (музыка, пение, шумовые эффекты и т.д.) путем изменения температуры, давления и других физических величин, плавно изменяющихся во времени. Телевизионный сигнал представляет собой последовательность очень коротких импульсов разного уровня. Уровень импульсов может принимать любое значение в некотором диапазоне от минимального до максимального. Если вершины соседних импульсов соединить прямой линией, то получится относительно плавно меняющийся график.

Факсимильные сигналы – световое пятно, сформированное с помощью источника света и системы оптических линз, перемещается вдоль изображения по строкам. Отражаясь от каждой элементарной площадки изображения, попадает на фотоэлемент и вызывает в его цепи ток. Значение тока зависит от яркости изображения.

б) Дискретные сигналы – это такие, которые в том же интервале времени имеют конечное число значений.

К таким сигналам относятся телеграфные и сигналы передачи данных.

Особенность этих сигналов состоит в том, что для каждого фиксированного момента времени t этот сигнал может принимать лишь два дискретных значения: +h и –h. Мгновенные значения телеграфного сигнала и сигнала передачи данных не могут быть иными. Например, рисунок 4.

Рисунок 4. Временная диаграмма дискретного сигнала

У этих сигналов будущие мгновенные значения непредсказуемы.

Сигналы классифицируются по информативности, т.е. содержат в себе информацию или не содержат.

. Математически сигнал описывается некоторой функцией времени, например, S(t).

Если эта функция заранее известна, то сигнал, который она представляет, называется детерминированным, т.е. известным, а математическое выражение, по которому для любого момента времени t можно вычислить значение электрического сигнала, называется математической детерминированной моделью этого сигнала.

Такие сигналы в себе информацию не содержат, а используются как контрольные, испытательные и в качестве переносчика информации (несущий).

Различают следующие основные типы детерминированных сигналов:

а) периодические – это сигналы, для которых можно указать период следования, т.е. промежуток времени, через который его значения повторяются. Простейшим и наиболее распространенным периодическим сигналом является гармоническое колебание, выраженное синусоидальной или косинусоидальной функцией времени;

б) почти периодическими сигналами называются такие, которые могут быть представлены в виде суммы гармонических составляющих с произвольными не кратными частотами. Для таких сигналов можно указать приближенный период повторения;

в) непериодические сигналы – это сигналы, для которых нельзя указать период следования. Форма такого сигнала может быть любой. Непериодический сигнал можно представить периодической функцией времени с бесконечно большим периодом (например, одиночный импульс).

Случайные сигналы – это такие, закон изменения которых заранее представить нельзя (речевой, вещания, телевизионный).

Только случайные сигналы содержат в себе информацию.

. Физическая характеристика сигнала – это описание любым способом его свойств.

Для систем передачи имеют важное значение лишь три основные характеристики:

1) Tс, – время передачи сигнала.

2) Дс = 10 lg , дБ – динамический диапазон сигнала, позволяющий определить пределы изменения мощности от максимального до минимального значения.

3) Fс = Fmax – Fmin (Гц) – ширина полосы частот передаваемого сигнала.

Произведение этих трех параметров называется объемом сигнала Vс.

Объем сигнала не имеет единицы измерения.

Пример перевода Дс в относительные единицы:

Д_С=10дБ

Д_С=10 lg

10=10 lg lg =10¹

Д_С=2дБ и т.д.

Объем сигнала изображается в трехмерной системе координат с соблюдением масштаба по всем осям (рисунок 5).

Рисунок 5. Графическое изображение объема сигнала.

Объем сигнала пропорционален объему информации им передаваемой.

Электрический сигнал, физический носитель информации, можно наглядно представить на временной и спектральной диаграммах.

а) Временная диаграмма – это зависимость мгновенных значений напряжения или тока от времени.

Рисунок 6. Рисунок 5.

Временная диаграмма Временная диаграмма

дискретного сигнала. аналогового сигнала

б) Спектральная диаграмма – это зависимость амплитуды напряжения или тока от угловой или текущей частоты.

в) Векторная диаграмма – это графическое изображение физических величин отрезками определенной длины и направления.

Рисунок 7. Спектральная диаграмма гармонического сигнала:

а) от fcл, Гц б) от _с, рад/с

Для закрепления изучаемого материала предлагается решить следующие задачи:

1)Дано: 3) Дано:

Тс=2с Тс=5с

Дс=10дБ Дс=20дБ

Fс=20Гц______________ Uc=20000_______________

Uс-? Изобразить на рисунке Fс-? Изобразить Uс на рисунке

2) Дано: 4) Дано:

Тс=4с Дс=10дБ

Дс=2дБ Fс=200 Гц

Fс=50Гц ______________ Uc=6000____

Uс-? Изобразить на рисунке Тс-? Изобразить Uc на рисунке

3. Для исследования явлений, происходящих в электрических цепях, по которым передаются, как правило, сложные сигналы, применяют метод разложения сложных периодических функций в ряд Фурье, сущность которого состоит в следующем: любой периодический сигнал можно рассмотреть как сумму простых гармонических составляющих:

U(t)=U₀+Um1 sin ( )+Um2 sin(2 ) + +Um3 sin(3 )+…+Umk sin (K )=U₀+ sin (K ),где

U₀-постоянная составляющая ряда Фурье.

U_m1, U_m2, U_m3…U_mk – амплитуды соответственно 1-ой, 2-ой, 3-ей…К-ой гармоник сигнала.

К - номер гармоники.

1- основная частота или первая гармоника.

2 …к - гармоники основной частоты.

1, 2, 3… к - начальные фазы гармоник.

Таким образом, видим, что ряд Фурье состоит из суммы гармонических составляющих.

Амплитуда и фаза гармонического колебания зависят от вида сигнала и оказываются разными для различных периодических сигналов с одним и тем же периодом следования.

Совокупность всех амплитуд ряда Фурье называется спектром амплитуд. Совокупность фаз этого ряда называется спектром фаз.

Спектры амплитуд и фаз можно представить графически, откладывая по оси Х значение частоты, а по оси Y значение амплитуды или фазы.

При построении спектральных диаграмм гармонического колебания необходимо учитывать три правила.

1. Спектр гармонического колебания представляется одиночной спектральной линией.

2. Высота спектральной линии определяется амплитудой сигнала.

3. Расположение спектральной линии по оси частот определяется частотой следования сигнала.

Рассмотрим построение временных и спектральных диаграмм для простейших синусоидальных сигналов.

Пример1.

Дано:

U(t)=Um1 sin ( )

Um1=1B

f=4кГц

Построить временную и спектральные диаграммы.

Для построения диаграмм соблюдаем по осям примерный масштаб.

1. Определяем период следования сигнала, зная, что

2) Выбираем удобный для построения временной диаграммы масштаб, учитывая начальную фазу сигнала, где знаменатель показывает на сколько частей следует разделить полупериод (в нашем примере на 4), а числитель – на какую часть переместить сигнал влево от нуля (в нашем примере на 1).

Рисунок 8. Временная диаграмма гармонического сигнала.

3) Строим спектральные диаграммы, соблюдая одинаковый масштаб по оси частот, а при построении спектра амплитуд и по оси ординат в соответствии с временной диаграммой.

Рисунок 9. Спектральные диаграммы гармонического сигнала.

а) спектр амплитуд; б) спектр фаз.

Пример 2.

Um1= 2В

f=3кГц

Построить временную и спектральные диаграммы.

1. При построении временной диаграммы необходимо учесть, что в данном случае начальная фаза – отрицательная.

Рисунок 11. Временная диаграмма гармонического сигнала.

2. Строим спектральные диаграммы.

Рисунок 12. Спектральные диаграммы гармонического сигнала.

а) спектр амплитуд; б) спектр фаз.

Задачи для решения.

1)Um=3B 2)Um=4B 3) Um=4B

f=2кГц f=1кГц f=5кГц

Построить временную и спектральные диаграммы.

Прежде чем приступить к построению спектральных диаграмм, необходимо построить временные диаграммы. Важным параметром периодической последовательности прямоугольных импульсов является скважность q, определяемая по формуле: q=

Т- период следования импульсов,

-длительность импульса.

Скважность q показывает во сколько раз период Т больше длительности импульса или какую часть периода составляет длительность импульса.

Построим временные диаграммы периодической последовательности прямоугольных импульсов разной скважности и частоты следования.

Пример1:

Um=1В

f=4кГц

q=2

Так как q= длительность импульса составляет половину периода

Определяем период Т:

Строим временную диаграмму, выбирая удобный масштаб.

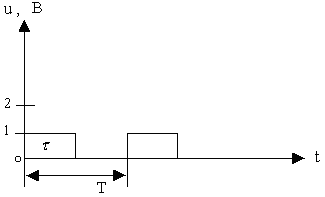
Рисунок 13. Временная диаграмма периодической последовательности

прямоугольных импульсов.

Пример 2:

Um=2В

f=2кГц

q=4

Т.к.

Следовательно, длительность импульса составляет ¼ Т, где

Строим временную диаграмму.

Рисунок 14. Временная диаграмма периодической последовательности

Прямоугольных импульсов.

Пример 3:

Обратим внимание, что q2 в 2 раза больше q1, при этом f=const. Диаграммы строим одну под другой, соблюдая одинаковый масштаб по осям, затем делаем соответствующие выводы.

Определяем 1 и 2, зная, что Т= const.

Строим временные диаграммы.

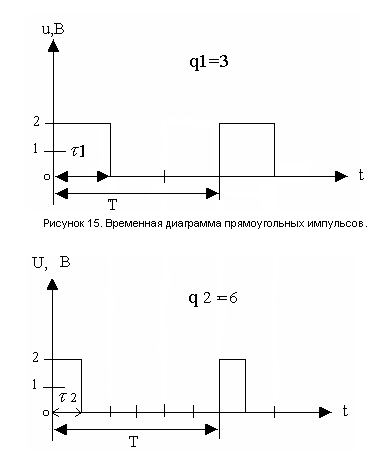
Рисунок 16. Временная диаграмма прямоугольных импульсов.

Из построения диаграмм видим, что при f=const и при увеличении скважности в 2 раза, Т остается постоянным, а длительность импульса уменьшается в 2 раза.

Пример 4.

Из данных видим, что q =const, а частота увеличивается в 2 раза. Следовательно, при увеличении частоты в 2 раза, период уменьшится в 2 раза, уменьшится и длительность импульса.

Строим временные диаграммы.

Рисунок 18. Временная диаграмма прямоугольных импульсов.

Для построения спектральных диаграмм необходимо рассчитать постоянную составляющую спектра Uо по формуле: Um- амплитуда сигнала, q-скважность.

Существуют следующие правила для построения спектральных диаграмм:

1. Спектр периодической последовательности прямоугольных импульсов линейчатый, т.е. содержит несколько спектральных линий.

2. Расстояние между соседними спектральными линиями определяется только частотой следования.

3. Каждая спектральная линия, кратная скважности, обращается в точку, т.е. в нуль, поэтому количество спектральных линий в лепестке q-1.

4. Частота, на которой спектральная линия обращается в нуль, определяется:

5. Частотный промежуток между двумя нулевыми значениями или между началом координат и первым нулевым значением называется лепестком.

6. Амплитуды в первом лепестке плавно уменьшаются, во втором и каждом последующем сначала плавно возрастают, а затем снова уменьшаются.

7. Лепесток всегда начинается с отметки 2 Uо.

Для расчета амплитуды каждой спектральной линии применяют формулу:

3,14

Um - максимальная амплитуда импульса,

К - номер гармоники,

q – скважность.

Рассмотрим следующий пример.

Дано:

Um=3В

f=5кГц

q=2____

Построить временную и спектральную диаграммы.

1) Строим временную диаграмму.

Рисунок 19. Временная диаграмма прямоугольных импульсов.

2) Выполняем расчет:

U₀=

U_mк=

U_m1=

U_m2=

U_m3=

U_m4=

3. По данным расчета, опираясь на выше перечисленные особенности, строим спектральную диаграмму.

4. Обычно на спектральной диаграмме показывают только два лепестка, т.к. максимум энергии передаваемого сигнала приходится именно на них.

Рисунок 20. Спектральная диаграмма периодической последовательности

прямоугольных импульсов.

4. За ширину спектра принимают такой интервал частот, для которого суммарная энергия содержащихся в нем гармоник сигнала составляет заданную долю от всей энергии сигнала. Для периодической последовательности прямоугольных импульсов энергия гармоник, частоты которых попадают в интервал от 0 до , составляет 95% энергии этого сигнала. Длина этого интервала равна ширине двух первых лепестков. Таким образом, ширина спектра периодической последовательности прямоугольных импульсов определится по формуле:

или

Из формулы следует, что чем меньше длительность прямоугольного импульса , тем шире его спектр.

Эта взаимосвязь между длительностью импульса и шириной его спектра сохраняется при любой форме импульса.

Спектр одиночного импульса показывает, что график спектральной плотности по форме совпадает с графиком огибающей спектра амплитуд импульсной последовательности.

Если представить одиночные импульсы с разной длительностью, то можно сделать важный вывод: чем меньше длительность сигнала, тем более широкую полосу частот занимают его гармонические составляющие, то есть тем больше энергия сигнала «размазана» по оси частот и тем более широкая полоса пропускания требуется для прохождения этого сигнала без искажений. Справедливо и обратное утверждение.

Проанализировать прохождение сигнала в виде одиночного импульса с разной длительностью и амплитудой: