Построение генераторов с линейными обратными связями.

Одним из главных преимуществ метода генерирования ПС–последовательностей максимальной длины является простота его реализации. Важнейшим классом ПСП являются последовательности, формируемые генераторами на основе регистров сдвига с линейными обратными связями –LFSR (Linear Feedback Shift Register) .

Используемый при анализе генераторов с линейными обратными связями математический аппарат – теория линейных последовательностных машин и теория конечных полей. Основными достоинствами этих генераторов являются

- простота аппаратурной реализации;

- максимальное быстродействие;

- хорошие статистические свойства формируемых последовательностей;

- возможность на их основе построение генераторов, обладающих свойствами, ценными при решении специфических задач защиты информации (формирование последовательностей произвольной длины, формирование последовательностей с предпериодом , формирование ПСП с произвольным законом распределения ,построение генераторов, обладающих свойством самоконтроля и т.п.)

Генератор с линейными обратными связями представляет собой устройство, со­стоящее из двоичных запоминающих элементов, образу­ющих регистр сдвига, и набора сумматоров по модулю два, служащих для формирования очередного значения последовательности. При этом сумматоры могут быть включены как во внешние цепи ОС генератора, так и в межразрядные связи элементов памяти регистра сдвига

Аппаратурный генератор ПСП, функционирующий в соответствии с выражением (2.1), содержит m—разрядный регистр сдвига (РС) и набор сумматоров по модулю два, включенные во внешние цепи обратной связи (ОС) (рис.2.1). В процессе функционирования генератора РС выполняет хранение и сдвиг вправо предшествующих символов последовательности, а сумматоры в цепи обратной связи производят вычисление значений очередных символов, которые последовательно записываются в самый левый разряд регистра .

рис.2.1.

Е сли последовательность состояний РС представить как последовательность m—мерных векторов А = (a₁,a₂,…a_m), где α_n€{0,1}, n=1,m то преобразование, осуществляемое схемой в некотором к – м такте работы, можно записать в матричной форме:

(2.2)

или в более компактном виде

(2.2а)

где

(2.2б)

Последовательное применение (2.1) позволяет найти состояние РС генератора в произвольный последующий такт работы:

(2.2в)

Аппаратурный генератор ПСП, в котором ОС включены в межразрядные связи элементов памяти регистра сдвига, представлен на рис.2.2.

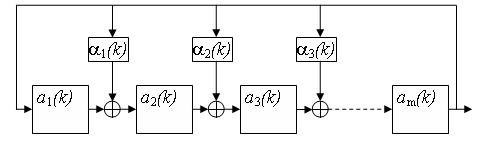
Рис.2.2

Для построения таких генераторов выражение 2.2, матрица V записывается как (2.3), а коэффициенты α определяются из обратного полинома .

(2.3)

Генераторы м-последовательности.

Циклические свойства генератора ПС последовательности определяются характеристическим многочленом:

, где α₀=α_m=1 . (2.4)

При соответствующем выборе коэффициентов α_i на основании характеристического полинома (2.4). который должен быть неприводимым и примитивным, последовательность имеет максимальную длину, равную . Такая последовательность называется M-последовательностью. Неприводимым называется такой многочлен φ(x) степени m, который не делится ни на какой другой многочлен от пониженной степени. Примитивным характеристический полином φ(x) будет в том случае, если полином делится на полином φ(x) только при . При этом необходимо, чтобы начальное состояние регистра сдвига не было нулевым, так как в противном случае генерируемая последовательность будет состоять из одних нулей, что соответствует тривиальному нулевому циклу генератору.

Основная задача синтеза генератора ПС—последовательности максимальной длины это нахождение многочлена φ(x), удовлетворяющего условию примитивности и неприводимости. Известно, что для данного m существует Ф(L)/m примитивных различных и неприводимых полиномов, где Ф(L)—функция Эйлера. Поскольку с ростом m число Ф(L) быстро увеличивается, то соответственно возрастает и количество многочленов φ(x) степени m, порождающих М—последовательности. Среди этого множества можно отыскать полиномы, имеющие наименьшее число нулевых членов. Данный случай характерен для минимальной конфигурации ГПСЧ, где в состав цепи ОС входит наименьшее число сумматоров по модулю два.

Необходимо отметить, что для формирования М–последовательности наряду с примитивным неприводимым полиномом φ(x) может использоваться и обратный ему . Получаемая в этом случае последовательность максимальной длины будет инверсна по отношению к последовательности, порождаемой φ(х).

Так как нулевое состояние регистра ГПК является запрещенным, максималь­но возможное число состояний устройства, а значит, и максимально возможная длина формируемой двоичной последовательности, снимаемой с выхода любого из триггеров, равны 2^m-1. В этом случае диаграмма состояний генератора со­стоит из одного тривиального цикла и цикла максимальной длины 2^m – 1.

В качестве примера на рис. 2.2.2 показаны альтернатив­ные структуры генераторов M-последовательностей для порождающего полинома _M(x)=x⁴x³1, а в табл. 2.2.1 представлена последовательность смены состояний их регистров сдвига при A_M⁽⁰⁾ = A⁽⁰⁾=1000. В соответствии с (2.2.2) для рассматриваемого примера имеем

. (2.5)

Для построения одноканального генератора М-последовательности получим систему логических уравнений:

(2.6)

На рис. 2.3 изображена схема гене­ратора М-последовательности для полинома в соответствии с системой логических уравнений (2.6),а в табл. 2.1 представлена последовательность смены состояний регистров сдвига при начальном состоянии A(0)=1000. Регистр сдвига реализован на D-триггерах, состояния которых изменяются по приходу на С-входы тактовых импульсов .

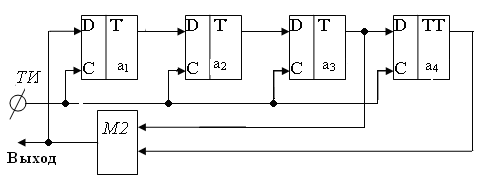
Рис.2.3

Таблица 2.1

№ такта	а1	а2	а3	а4	Выход
0	1	0	0	0
1	0	1	0	0	0
2	0	0	1	0	1
3	1	0	0	1	1
4	1	1	0	0	0
5	0	1	1	0	1
6	1	0	1	1	0
7	0	1	0	1	1
8	1	0	1	0	1
9	1	1	0	1	1
10	1	1	1	0	0
11	1	1	1	1	0
12	0	1	1	1	0
13	0	0	1	1	1
14	0	0	0	1	1
15	1	0	0	0	0

Из табл.2.1 следует, что длина формируемой последовательности равна 15, т.е. через 15 тактов регистр устанавливается в начальное состояние.

Перейдём к рассмотрению свойств последовательностей максимальной длины .

1. Период М–последовательности, формируемый в соответствии с выражением

, k = 0, 1, 2, 3, . . . ,

где а_k€{0,1}–символы последовательности; α_i€{0,1}–коэффициенты, определяемые примитивным неприводимым порождающим полиномом φ(х), для которого m=deg φ(х), равен 2^m - 1.

2. Для заданного φ(х) существует L различных М—последовательностей, сдвинутых относительно друг друга.

3. Число единичных символов на периоде М—последовательности равно 2^m-1, а нулевых—2^m-1-1. Вероятности появления 1 и 0 определяются выражениями

;

и при увеличении m достигают значений сколь угодно близких к 0,5.

4. В псевдослучайной последовательности максимальной длины серии из одного символа (1 или 0) встречаются 2^m-2 раз, из двух единиц или нулей 2^m-3 и т.д. Серии из m-1 нулей и m единиц встречаются лишь по одному разу. Сравнивая выражения для оценки вероятности появлении серий из l одинаковых символов, можно убедиться в их практической эквивалентности.

5. Для каждого целого s(l≤s<L) существует такое целое r≠s (l≤r<L), что {a_i}{a_i-s}={a_i-r}. Данное свойство обычно называют свойством сдвига и сложения.

6. Автокорреляционная функция М–последовательности определяется выражением

7. Децимацией последовательности {a_i} по индексу q(q=1, 2, 3,…) называется формирование новой последовательности {bi} из q—х элементов {a_i}, т.е. b_k=a_kq. Если {b_i} является нулевой последовательностью, то она порождается полиномом ψ(х), и имеет период L/(L,q), где (L,q)наибольший общий делитель L и q. При (L,q)=1период {b_i} равен L=2^m-1, где m=deg φ(х), и децимация называется собственной или нормальной.

Результатом всякой нормальной децимации является М–последовательность периода L, порождаемая примитивным неприводимым полиномом ψ(х). При этом если децимация выполняется над последовательностью, сдвинутой на j тактов относительно исходной {a_i}, то получаемая последовательность будет также сдвинутой на некоторое число j тактов по сравнению с {bi}. Иначе говоря, независимо от того, какой именно сдвиг последовательности, порождаемой полиномом φ(х), выбран, результатом ее всегда оказывается М–последовательность, порождаемая полиномом ψ(х). В частности, при децимации характеристической М—последовательности {a_i}*, порождаемой многочленом φ(х), получается также характеристическая последовательность {b_i}*, соответствующая полиному ψ(х).

Рассмотрим несколько разновидностей М—последовательностей, формируемых в результате нормальных децимаций. Поскольку децимация по индексу q будет давать тот же результат, что и децимация по q(mod L), ограничимся q≤L. Прежде всего, очевидно, что децимация по единичному индексу будет равна исходной последовательности b_k=a_k*l=a_k. Результатом децимации характеристической последовательности по индексу 2 будет исходная характеристическая последовательность b_k*=a_2k*=a_k*. Следовательно, для произвольной последовательности {a_i} существует такое n, при котором ее децимация {a_i} по индексу 2 равна сдвигу на n тактов a_k2=a_k-n. Отсюда следует, что характеристическая последовательность {a_i}* есть результат сдвига исходной {a_i} на 2*n тактов, a*_k=a*_k-2n. Тогда, поскольку для любого s a*_2k^s=a_k, справедливо равенство a_2k^s=a_k-r, где величина сдвига r зависит от s. В общем случае М—последовательность периода L может быть сформирована из исходной посредством ее децимации по нечетному индексу q.

Среди децимации по четному индексу выделяют случай q=L-1, при котором b_k=a_k(l-1)=a_-k. Иными словами, последовательность {b_i} является инверсной к {a_i} и порождается полиномом ψ(х), обратным к φ(х), ψ(х)=φ (х).

Данное свойство это—тест, позволяет различать М—последовательности и последовательности случайных двоичных цифр. Пусть а₀,а₁,…,а_n-1—сегмент М–последовательности периода L=2^m-1, где n<L. Составим матрицу:

где m<b<n/2. ранг данной матрицы меньше величины b, что следует из наличия линейной зависимости между символами М—последовательности. С другой стороны, если а₀а₁…а_n-1—последовательность равновероятных двоичных случайных цифр, то вероятность того, что rang(M)<b, не превышает 2^2b-n-1 и при соответствующем выборе b и n оказывается весьма незначительной величиной.

Таким образом, вопрос rang(M)<b? является тестом, с помощью которого по ограниченному числу элементов М—последовательности можно показать, ее отклонение от абсолютной случайности. Например, при m=11, L=2^m-1=2047 и b=15 для М—последовательности rang(M)<b, начиная с n=50, тогда, как вероятность получить такой же результат для случайной последовательности не превышает 2^-21.

Многоканальные генераторы М-последовательностей.

Если последовательность состояний регистра сдвига представить как последовательность m—мерных векторов А=(a1,a2,…am), где an€{0,1}, n=1,m то преобразование, осуществляемое схемой в некотором к–ом такте работы, можно записать в матричной форме:

(2.5)

или в более компактном виде

, (2.6)

где

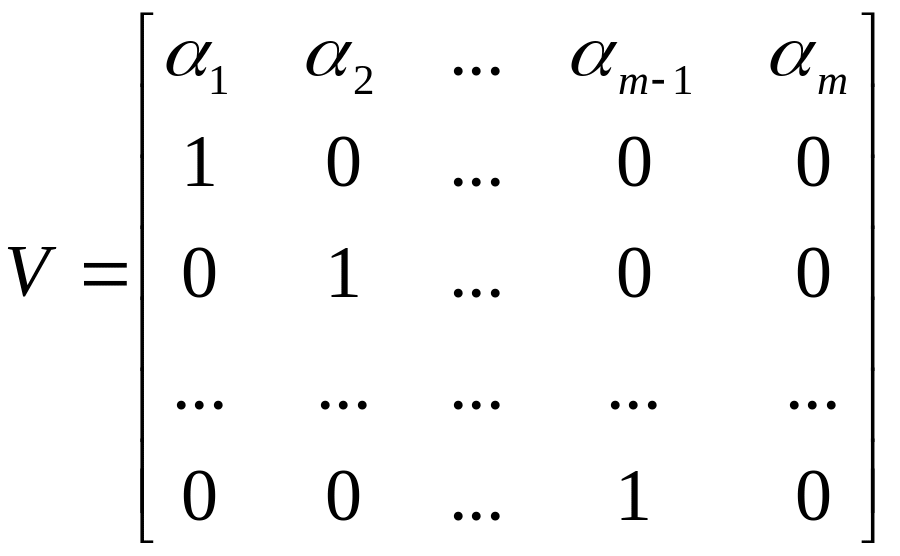(2.7)

Таким образом, при последовательном применении выражения (2.6), можно определить состояние регистра сдвига генератора в произвольный последующий такт работы:

, (2.8)

где s – это величина сдвига.