2.1. Предел функции в точке, односторонние пределы, предел функции в бесконечности.

Понятие предела является основополагающим в математическом анализе.

Определение 1.1 (конечного предела) . Число А называется пределом функции f(x) при x, стремящемся к предельной точке a, записывается

если

(2.1)

Смысл условия (2.1) в следующем: когда аргумент х принимает значения близкие к a (кроме самого a) , значения функции должны быть близки к числу А. Рассмотрим

Пример 1.1. Доказать, что

Покажем, что для произвольного положительного ε можно взять . Выполнение условия (2.1) следует из справедливости цепочки эквивалентных неравенств:

Предел функции может и не существовать.

Рис. 2.1

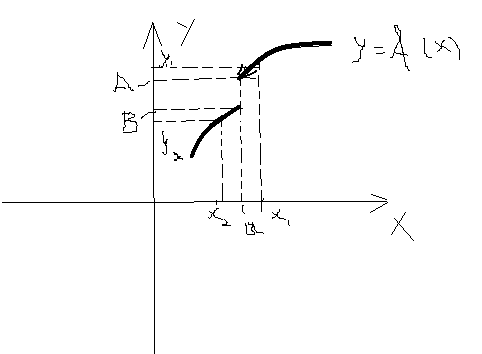
Рис. 2.2

На рисунке 2.1 изображена ситуация, где функция f(x) не определена в точке а, однако, предел при x → a существует и равен А. Рисунок 2.2 иллюстрирует случай, когда f(x) определена при х = а , но предел при x → a не существует т.к. при стремлении х к точке а слева все значения f(x) близки числу А, а при приближении переменной х к а справа значения f(x) приближаются к числу В, и , следовательно, нет такого числа, к которому бы стремились значения f(x), при произвольном стремлении х к а.

Следующие утверждения характеризуют функцию, имеющую предел.

Определение 2.2. Функция называется ограниченной в точке a, если существует числа δ > 0 и M > 0 такие, что |f(x)| < M для любых x из U(δ,a).

Теорема 2.1. (об ограниченности функции, имеющей предел). Если существует

то f(x) ограничена в точке а.

Определение 2.3 (одностороннего предела) . Число А называется пределом функции f(x) при x, стремящемся к a слева (справа), записывается

если

На рисунке 2.2 изображена ситуация, когда

Для обозначения односторонних пределов часто используются обозначения

Из определений 2,2 вытекает следующий критерий существования предела

Теорема 2.3 (критерий существования предела). Для существования предела

функции f(x) при x → a необходимо и достаточно, чтобы существовали равные между собой односторонние пределы

и .

Рассмотрим другие разновидности предела функции.

В определении 2.1 точка а считается конечной, дадим определение предела для случая, когда а =

Определение 2.4 (предела для бесконечной предельной точки). Число А называется пределом функции f(x) при x, стремящемся к ,,записывается

,

если

.

Например,

Иногда употребляют запись x → , понимая под ней x → или x → .

Дадим теперь определение предела для случая, когда А = .

Определение 2.5 (бесконечного предела или бесконечно большой функции) .Запись

означает, что

(2.2)

Если выполняется хотя бы одно из условий (2.2), то функция f(x) называется бесконечно большой (б.б.) при x → a.

Например,

В дальнейшем в записи

числа а и А будут предполагаться как конечными так и бесконечными, а предел будет пониматься в соответствии с определением, отвечающим виду а и А.

2.2.. Бесконечно малые и бесконечно большие величины. Их сравнение.

Определение 2.6 .Функция называется бесконечно малой (б.м.) при x → a, если

Зная определение предела функции при , можно дать развернутое определение бесконечно малой величи­ны:

y=f(x)- б.м. при x → a

Обычно для обозначения бесконечно малых используют малые греческие буквы. Рассмотрим свойства бесконечно малых функций.

Определение 2.6 .Функция называется бесконечно большой (б.б.) при x → a, если

Теорема 2.5 (свойства бесконечно малых). Справедливы следующие свойства

1^О. Сумма конечного числа бесконечно малых есть бесконечно малая т.е. если α₁(x), α₂(x),… ,α_n(x) – бесконечно малые при x → a , то β(x)= α₁(x) + α₂ (x)+… + α_n(x) тоже бесконечно малая при x → a

2^О. Произведение бесконечно малой и ограниченной функций есть бесконечно малая т.е. если. α(x) - бесконечно малая при x → a, а f(x) ограниченная в точке а, то β(x)=f(x)· α(x) тоже бесконечно малая при x → a.

3^О. Функция обратная к бесконечно малой есть бесконечно большая т.е. если α(x) - бесконечно малая при x → a, то β(x)=1/ α(x) бесконечно большая при x → a.

Доказательство приведенных свойств проводится примерно по одной схеме с использованием определений. Для примера докажем свойство 2^О.

Пусть фиксировано произвольное положительное число и пусть и М- какие-нибудь числа из определения ограниченности f(x) такие, что

|f(x)| < M для всех х: |x-a| <

В силу того, что . α(x) - бесконечно малая, по числу найдется такое, что

для всех х: |x-a| <

Положим , тогда для всех х:|x-a| < имеем

Отсюда с учетом произвольности следует, что бесконечно малая при x → a.

Доказательство остальных свойств полезно выполнить самостоятельно в качестве упражнения. Приведенные свойства будем использовать в дальнейшем для доказательства свойств пределов.

Теорема 2.6 (свойства бесконечно больших). Справедливы следующие свойства

1^О. Сумма конечного числа бесконечно малых есть бесконечно малая т.е. если α₁(x), α₂(x),… ,α_n(x) – бесконечно большие при x → a , то β(x)= α₁(x) + α₂ (x)+… + α_n(x) тоже бесконечно большая при x → a

2^О. Функция обратная к бесконечно большой есть бесконечно малаят.е. если α(x) - бесконечно большая при x → a, то β(x)=1/ α(x) бесконечно малая при x → a.

Теорема 2.7 (о представлении функции, имеющей предел) . Для того, чтобы существовал

необходимо и достаточно, чтобы

f(x) =A + (x) (1)

для некоторой б.м. при x → a функции (x).

Доказательство. Необходимость. Пусть . Это означает

( *)

.Положим α(x) =f(x) - A , тогда из (*) сразу следует, что α(x) бесконечно малая. Отсюда вытекает предсталение f(x) в виде (1).

Достаточность условия (1) сразу следует из определения предела.

Сравнение бесконечно малых функций. Символы о и О.

Определение 2.7. Б.м. функции ά(x) и β(x) называются эквивалентными при , если

Эквивалентность ά(x) и β(x) обозначают:  ~ β , Например, в дальнейшем буде показано, что при ,→0

Sin  ~ ,

tg  ~ ,

ln(1+) ~ .

Определение 2.8. Б.м. функцию ά(x) называют бесконечно малой более высокого порядка, чем β(x) (обозначается ά(x)=o( β(x)) ), если

Определение 2.9. Б.м. функцию ά(x) называют бесконечно малой одного порядка с β(x) (обозначается ά(x)=О( β(x)) ), если существует такое число С ≠ 0, что