1.3.7.Расчет ригеля на прочность по наклонным сечениям
Расчет ригеля на поперечную силу Qmax по наклонным сечениям обеспечивает определение шага поперечных стержней. Число поперечных стержней в сечении n равно количеству принятых плоских сварных каркасов в ригеле.
Диаметр поперечных стержней dw принимается из условия свариваемости с рабочей продольной арматурой.
Тогда площадь поперечных стержней Asw=n.Asw1,
где n – количество каркасов в ригеле;
Asw1 – площадь поперечного сечения стержня;
Назначается шаг поперечных стержней на приопорных участках согласно конструктивным требованиям
S1
должен быть кратен 50мм с длиной приопорного
участка l1=lр/4.
На основании вышеприведенного расчета на прочность по нормальным сечениям установлено, что рабочая продольная арматура составляет
4 Ø18 А-III с As=10,18см2. На рис. 8 показано размещение этой арматуры в нижней зоне ригеля. В верхней зоне предусмотрена конструктивная арматура в виде каркаса К-1. Диаметр поперечных стержней из условия свариваемости принимаем Ø5 А-I с As=19,6мм2.
С учетом двух каркасов по обе стороны ригеля
Asw=n.Asw1=19,6.2=39,2мм2=0,392см2.
Назначим шаг
поперечных стержней S1
на приопорных участках согласно
конструктивным требованиям
S1 должен быть кратен 50мм, назначаем S1=250мм.
Длина приопорного участка l1=lр/4=5,84/4=1,37м. Принимаем l1=1,5м, так как шаг поперечных стержней S1=250мм.
Уточним шаг поперечных стержней.
1) Определим величину Мb
Мb
=
=2.(1+0).0,9.0,9.10-6.475.7152=393,38кНм,
где φf =0, φb2=2 – для тяжелого бетона (п. 3.31 [1]);
2)
Qb,min=
=0,6.(1+0).0,9.0,9.10-3.475.715=165,05кН,
где
φb3
=0,6 – для тяжелого бетона.
3) Погонное усилие:
=
=27,44кН/м
4) Проверим усилие:
=27,44кН/м
≥
=
=115,42кН/м
– условие не выполняется.
Назначаем шаг поперечных стержней S1=50мм, тогда
=
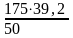=137,2кН/м>
=
=115,38кН/м
– условие выполняется.
5) Принимаем q1=qр=105кН/м,
6) Определим длину проекции наклонного сечения, если 0,56. =0,56.137,2=
76,832кН/м<q1=105кН/м, то
с=
=
=1,27м.
7) Сравним с=1,27≤3,33.h0=3,33.0,715=2,38м
Условие выполняется, для дальнейшего расчета принимаем с=1,27
8) Вычислим длину проекции наклонной трещины:
c0=
=
=1,69м.
9) Принимаем длину проекции наклонной тещины исходя из трех условий:
а) c0<c; c0=1,69м>с=1,27м;
б) c0<2h0; c0=1,69м>2h0=2.0,715=1,43м;
в) c0>h0; c0=1,69м>h0=0,715м;
Из анализа 3-х условий назначаем c0=1,27м.
10) Проверим условие прочности Qmax-qр.c≤ +qsw1.c0
Qmax-q1.c=287,7-105.1,27=154,35кН/м,
+qsw1.c0=
+137,2.1,69=541,61кН
Следовательно, 154,35кН<541,61кН – условие выполняется.
11)
Проверим условие s1≤
smax,
где smax=
=
=1025,51мм,
φb4=1,5 – для тяжелого бетона.
s1=150мм< smax=1025,51мм – условие выполняется.
12) В средней части пролета плиты шаг поперечных стержней s2 согласно конструктивным требованиям s2 не более (3/4)h=(3/4)800=600мм и не более 500мм; принимаем s2=500мм.
13) Проверим прочность сечения по наклонной сжатой полосе между трещинами из условия:
Qmax=287,7кН≤0,3.φw1.φb1.Rb.γb2.bр.hор=0,3.1,024.0,896.11,5.0,9.475.715.10-3=
=967,54кН,
где φw1=1+5.α.μw=1+5.8,75.0,00055=1,024<1,3;
μw=Asw/(b.s1)= 39,2/(170.150)=0,00055;
α=Еs/Еb=21.104/24.103=8,75;
φb1=1-β. Rb. γb2=1-0,01.11,5. 0,9=0,896, β=0,01 – для тяжелого бетона.
То есть 287,7кН<967,54кН, прочность по наклонной сжатой полосе обеспечена.
На рис.8 показано армирование ригеля, состоящее из двух каркасов КР1 и соединительных стержней Ø5 Вр-I (сеткой С1), гнутой по профилю полок.