Развёртка сферы и тора.

Суть построения состоит в том, что мы должны построить развёртку поверхности, разделив её на несколько долей (как апельсин). И, таким образом, строим развёртку одной доли, другие – её повторяют.

Итак, делим гор. пр-ию поверхности на 8 равных частей. Надо заметить, что развёртка получится тем точнее, чем на большее количество частей мы разделим поверхность.

Одну из частей делим снова пополам. Таким образом, получаем одну целую дольку. Будем строить её развёртку.

• На фронтальной пр-ии очерковую линию делим с помощью произвольно взятых точек (чем их >, тем точнее развёртка);

• Находим горизонт. пр-ии данных точек.

• Затем на свободном месте листа проводим горизонтальную линию - экватор сферы. Отмечаем произвольно некоторую точку 1;

• Проводим через неё вертикальную линию ();

• Откладываем на этой линии расстояния, взятые с фронтальной пр-ии, получим высоту доли. А вправо и влево – расстояния, взятые с гор. пр-ии.

• Далее точки соединяем плавной линией с помощью лекало.

Таких долей должно быть 8.

Лекция 12 Проекции с числовыми отметками.

Способы изображения, рассмотренные ранее, оказываются неприемлемыми при проектировании таких инженерных сооружений, как полотно железной или шоссейной дорог, дамбы, аэродромы, т.е. в тех случаях, когда высота объекта существенно меньше его размеров на плане. Изображением только плана инженерного сооружения и ограничиваются в методе проекций с числовыми отметками.

Также, проекции с числовыми отметками встречаются в геодезии, в военном деле, в картографии, одним словом, всё, что связано с геометрией земли.

Сущность метода заключается в том, что геометрический образ ортогонально проецируется только на одну горизонтальную плоскость пр-ий (план), называемую обычно плоскостью нулевого уровня - П₀. Проецирование ведётся ||-ми лучами -но данной плоскости.

Ч тобы по проекциям т-ек судить о положении этих т-ек в пространстве, рядом с проекцией каждой т-ки проставляется цифра – отметка, указывающая расстояние в метрах от т-ки до плоскости нулевого уровня. Т-ки, расположенные над плоскостью нулевого уровня имеют положительные отметки, а т-ки, расположенные ниже плоскости П₀ - отрицательные отметки. Т-ки, лежащие в плоскости уровня имеют нулевую отметку.

Числовые отметки могут быть мерные (мм, см, м) или одна единица может быть задана в виде отрезка.

Числовые отметки играют роль фронт-ой пр-ии.

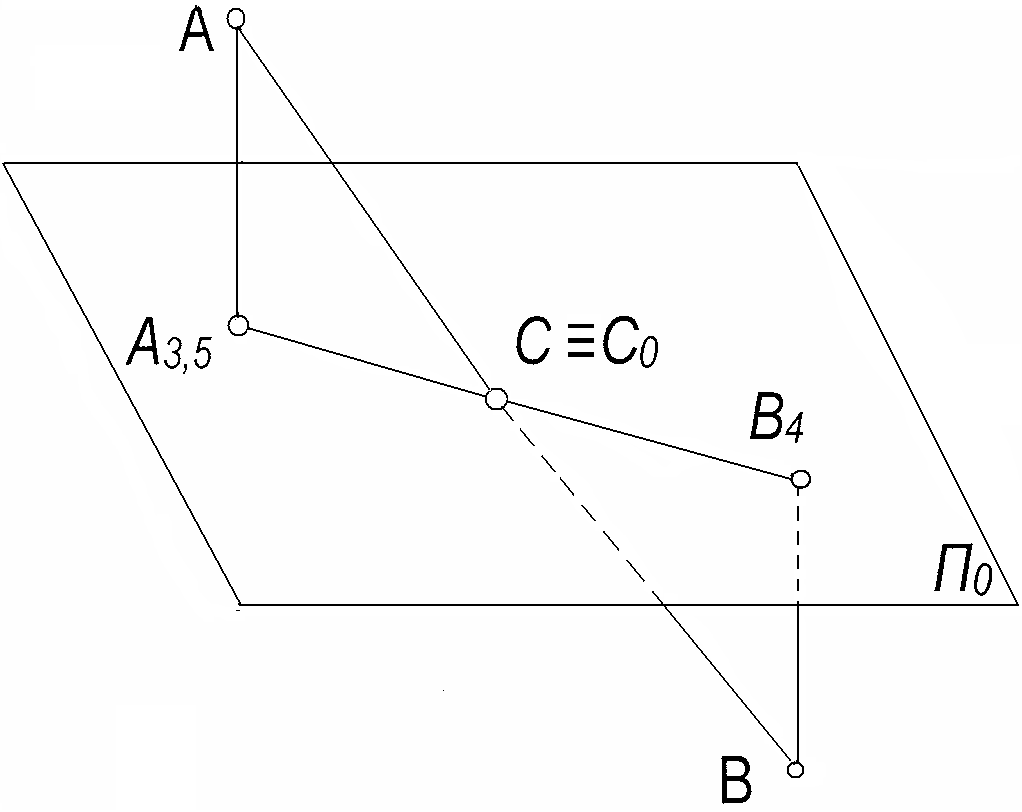
Изображение прямой.

Прямая линия может быть задана пр-ми двух любых её т-ек. В пространстве расположена точка А, высота её 3 единицы. Проецируем её на пл-ть П₀  А_3. Т.о. т-ка А расположена над пл-тью П₀ на высоте 3 единицы. Т-ка В находится под пл-тью П₀ В_-4. Соединяем данные т-ки  получили прямую АВ. Также появилась т-ка С – т-ка пересечения прямой АВ с пл-тью П₀, её отметка = 0. Т.о. т-ка С₀ –это след прямой АВ. Прямая, соединяющая пр-ии А₃ и В₄ т-ек А и В, является проекцией отрезка АВ - прямой линии.