Непозиционные

Люди научились считать очень давно. В последствии появилась потребность в записи чисел. Количество предметов изображалось нанесением черточек, засечек на какой-нибудь твердой поверхности. Чтобы два человека могли точно сохранить некоторую числовую информацию, они брали деревянную бирку, делали на ней нужное число зарубок, а потом раскалывали бирку пополам. Каждый уносил свою половинку и хранил ее. Этот прием позволял избегать спорных ситуаций. Археологами найдены такие записи при раскопках. Они относятся к 10-11 тысячелетию до н.э.       

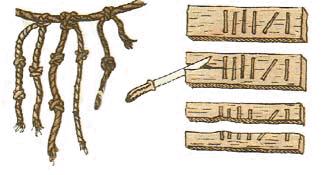
Ученые назвали такую систему записи чисел единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу.

Позднее эти значки стали объединять в группы по 3, 5 и 10 палочек. Поэтому возникали более удобные системы счисления.

Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел использовались специальные значки – иероглифы. Каждый такой иероглиф мог повторяться не более 9 раз. Такая система счисления называется древнеегипетская десятичная непозиционная система счисления.

Примером непозиционной системы счисления, которая сохранилась до наших дней, может служить система счисления, применявшаяся более двух с половиной тысяч лет назад в Древнем Риме. Она называется римская система счисления.

В основе лежат знаки I(1), V(5), X(10), L(50), C(100), D(500), M(1000).

Римскими цифрами пользовались очень долго, сегодня они используются в основном для наименования знаменательных дат, томов, разделов и глав в книгах.

Правила составления чисел в римской системе счисления: 

1. Идущие подряд несколько одинаковых цифр складываются(группа первого вида).

2. Если слева от большей цифры стоит меньшая, то от значения большей отнимается значение меньшей цифры(группа второго вида).

3. Значения групп и цифр, не вошедших в группы первого и второго вида складываются.

Непозиционные системы счисления имеют ряд существенных недостатков:

1. Существует постоянная  потребность введения новых знаков для записи больших чисел.

2. Невозможно представлять дробные и отрицательные числа.

3. Сложно выполнять арифметические операции, так как не существует алгоритмов их выполнения. В частности, у всех народов наряду с системами счисления были способы пальцевого счета, а у греков была счетная доска абак – что-то наподобие наших счетов.

Перевод из одной системы счисления в другую

Соответствие чисел, записанных в различных системах счисления:

Деся-тичная	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Восьме-ричная	0	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17	20
Двоичная	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111	10000
Шестнад-цатерич-ная	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

Для записи шестнадцатеричных цифр можно использовать также строчные латинские буквы a-f.